Vector Algebra : Understanding Direction

maths > vector-algebra

Understanding Direction

what you'll learn...

Overview

Understanding Direction

» Independence of Quantities along Orthogonal Directions

    → For a vector, any changes along one axis affect only the component along that axis and do not affect the components along other axes, as the axes are orthogonal

» Effect of Direction:

    → Addition involves right-triangles and Pythagorean identity

    → Product between quantities involves either one of component in parallel or perpendicular

orthogonality

The fundamental mathematical operations for vectors are introduced. Let us see how having direction component affects these fundamental operations in vectors.

From a starting position, a person walks $5$ $5$ m east and then takes the following path

• $3$ $3$ m north

• $4.2$ $4.2$ m south

• $\frac{3}{4}$ $3/4$ m north

At this end position, how far is the person away from the starting point in the east direction ?

The answer is ' $5$ $5$ m '– as the person moved $5$ $5$ meter east and then all his movements were in directions north and south.

Note that any change in north and south direction does not affect the magnitude in east direction.

Independence of Quantities along orthogonal directions: For a vector, any changes along one axis affect only the component along that axis and do not affect the components along other axes, as the axes are orthogonal.

independence explained

A ball has a velocity in x-axis $20$ $20$ m/sec. It also has an unknown velocity in y-axis. In $2$ $2$ seconds, how far the ball would travel along x-axis? Can it be calculated without knowing the velocity along y-axis?

Yes. The answer is ' $20 \times 2$ $20xx2$ ' along the x-axis. The velocity vector causes displacement vector. The component of 'displacement' in one direction is only caused by the component of 'velocity' in that direction.

A person walks $5$ $5$ m at $30^{\circ}$ $30^@$ angle to east. Then he turns $90^{\circ}$ $90^@$ clockwise and walks for 2m. What is the distance from the starting point along the direction $30^{\circ}$ $30^@$ angle to east?

The answer is ' $5$ $5$ m' – as the person moved only $5$ $5$ meter in the direction $30^{\circ}$ $30^@$ angle to east. He walked in perpendicular to the direction after that.

A person walks $5$ $5$ m at $30^{\circ}$ $30^@$ angle to east. Then he turns $40^{\circ}$ $40^@$ clockwise and walks for 2m. What is the distance from the starting point along the direction $30^{\circ}$ $30^@$ angle to east?

The $2$ $2$ m walk is not at right angle to the direction in question. Solving this with vectors is explained with an illustration later.

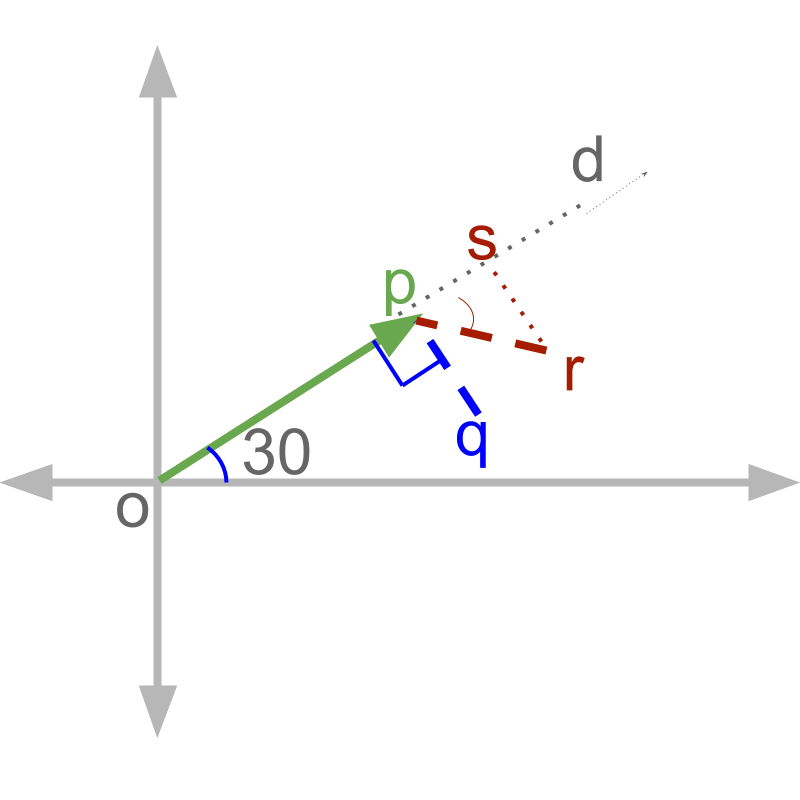
Take two persons $A$ $A$ and $B$ $B$ start from the point $o$ $o$ and walks to $p$ $p$ in direction the $d$ $d$ .
• Person $A$ $A$ turns at right angle and walks to $q$ $q$
• Person B turns at an angle $40^{\circ}$ $40^@$ and walks to $r$ $r$

The displacement along direction $d$ $d$ is asked.
• For person $A$ $A$ , the displacement along $d$ $d$ is between points $o$ $o$ and $p$ $p$
• For person $B$ $B$ the displacement along $d$ $d$ is between points $o$ $o$ and $s$ $s$ , as the segment $\bar{p r}$ $bar(pr)$ has component $\bar{p s}$ $bar(ps)$ along direction $d$ $d$ .

The component which is in perpendicular to a direction does not affect the component in the direction. The directions which are at $90^{\circ}$ $90^@$ angle are referred to as orthogonal directions.

parallel & perpendicular

In arithmetic operations like addition, subtraction, multiplication by a scalar, and product of vectors, – the results are computed for

• components in parallel

• components in perpendicular

Each of these two components interact differently.

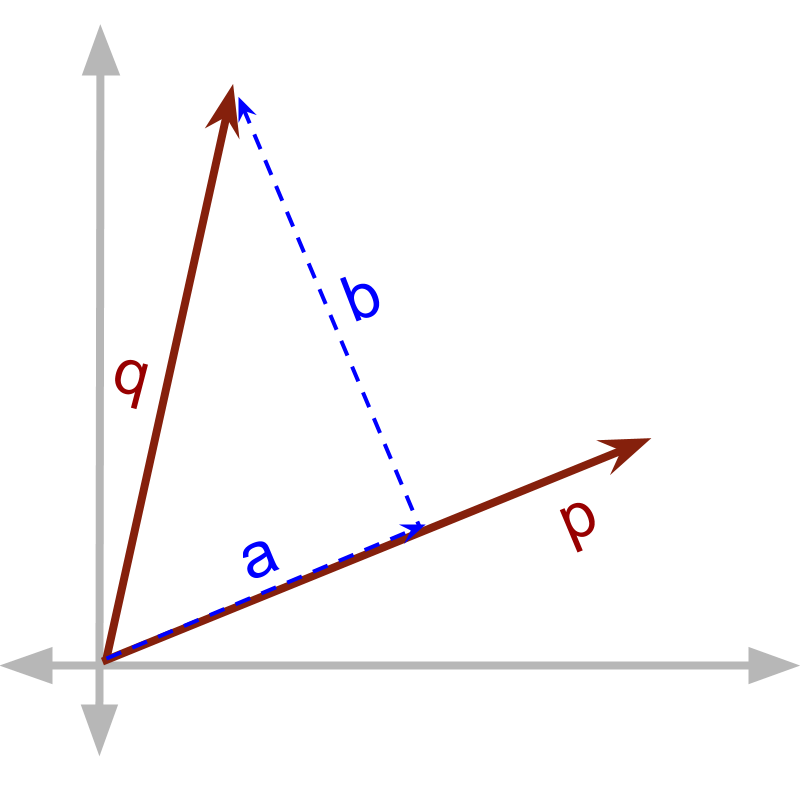
How does direction affect vector quantities in multiplication?

At an abstract level, there are two products possible. Given multiplicand $\vec{p}$ $vec p$ and multiplier $\vec{q}$ $vec q$ . $\vec{q}$ $vec q$ is split into $\vec{a}$ $vec a$ and $\vec{b}$ $vec b$ , such that
   $\vec{q} = \vec{a} + \vec{b}$ $vec q = vec a + vec b$ and
   $\vec{a}$ $vec a$ is in parallel to $\vec{p}$ $vec p$
   $\vec{b}$ $vec b$ is in perpendicular to $\vec{p}$ $vec p$

two forms of multiplications are defined for each of these two components.

• one with component in parallel to the other, called vector dot product. $\vec{p} \cdot \vec{q} = \vec{p} \cdot \vec{a}$ $vec p cdot vec q = vec p cdot vec a$

• another with component in perpendicular to the vector, called vector cross product. $\vec{p} \times \vec{q} = \vec{p} \times \vec{b}$ $vec p times vec q = vec p times vec b$

summary

Effect of direction: In mathematical calculations, vectors have the following properties
• A vector is represented as components along orthogonal directions.

• In vector addition, components in parallel add up and components in perpendicular are combined using Pythagoras Theorem.

• Two types of vector multiplication are defined,

• In vector dot product, only the component of the vector in parallel to the other vector takes part in multiplication.

• In vector cross product, only the component of the vector in perpendicular to the other vector takes part in multiplication.

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed