Vector Algebra : Cross Product with Direction removed

maths > vector-algebra

Cross Product with Direction removed

what you'll learn...

Overview

Cross Product With Direction Removed

» By definition, cross product is a vector

» Some applications may specify a scalar in the multiplication of components in perpendicular. In such cases, the direction is removed from the vector cross product.

example

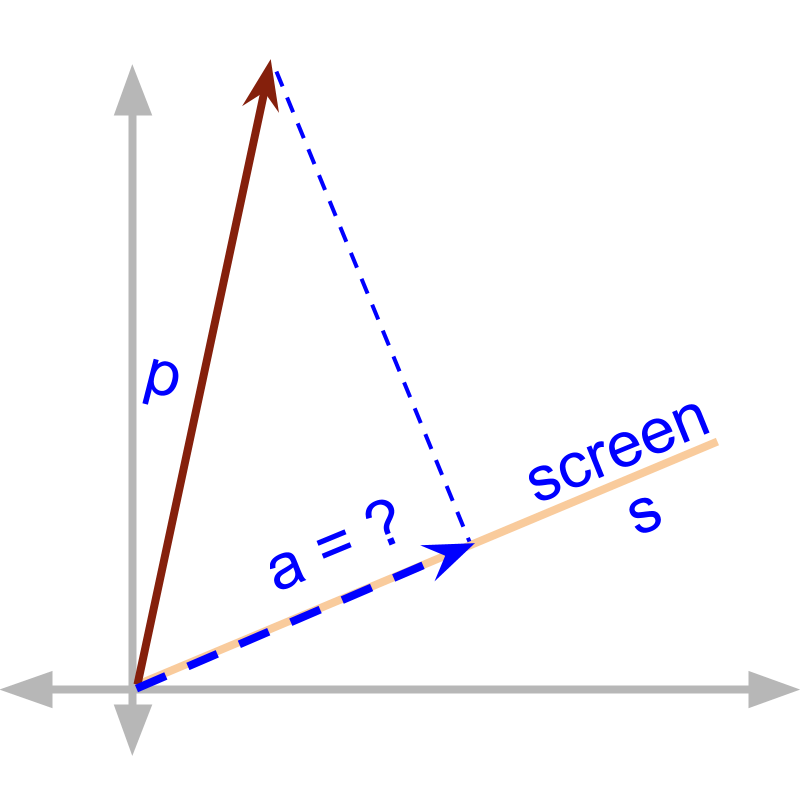
An object by position vector $\vec{p}$ $vec p$ is at a distance from a screen. The screen is given by unit vector $\vec{s}$ $vec s$ . The distance of the object from the screen is a vector that terminates at the object and at $90^{\circ}$ $90^@$ angle to the screen.

Note: In physics - Kinematics, distance and displacement are defined as scalar and vector. In coordinate geometry, distance from an object to another is a vector.

Given $\vec{p}$ $vec p$ and the screen $\hat{s}$ $hat s$ . The magnitude of distance of object from the screen is $| \vec{p} \times \hat{s} |$ $|vec p xx hat s|$ $= | p | \sin θ$ $= |p| sin theta$

An object by position vector $\vec{p}$ $vec p$ is at a distance from a screen. The screen is given by unit vector $\vec{s}$ $vec s$ We saw that the distance is a vector and the length of the distance is $| \vec{p} \times \hat{s} |$ $|vec p xx hat s|$ . The direction of the distance vector is 'unit vector along $\vec{p} - (\vec{p} \cdot \hat{s}) \hat{s}$ $vec p - (vec p cdot hat s) hat s$ '.

Another Example

The magnetic field is given by $\vec{B}$ $vec B$ (a vector quantity).

The velocity of the wire moving in the magnetic field is $\vec{v}$ $vec v$ (a vector quantity).

The EMF (electro-magnetic force or the voltage) induced in the wire of length $L$ $L$ is given by

$EMF = L | \vec{v} \times \vec{B} |$ $text(EMF) = L |vec v xx vec B |$

Note that the EMF is a scalar quantity.

In this, $\vec{v}$ $vec v$ has component parallel and another component perpendicular to the magnetic field $\vec{B}$ $vec B$ . Only the perpendicular component interacts with the magnetic field and results the EMF. That is the reason, the equation has cross product.

The created EMF is by definition a scalar quantity. So, the magnitude of the cross product is used.

summary

Distance using Cross Product: For a vector $\vec{p}$ $vec p$ and a direction given by unit vector $\hat{s}$ $hat s$ , the magnitude of distance of point given by $\vec{p}$ $vec p$ to the direction $\hat{s}$ $hat s$ is $| \vec{p} \times \hat{s} |$ $|vec p xx hat s|$ .

Vector cross product, by definition, is a vector. Depending on the application requirement, the direction can be removed.

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed