Vector Algebra : Vector Addition

maths > vector-algebra

Vector Addition - First principles

what you'll learn...

Overview

Vector Addition: First Principles

» Components in parallel add and component in perpendicular combine as right triangle
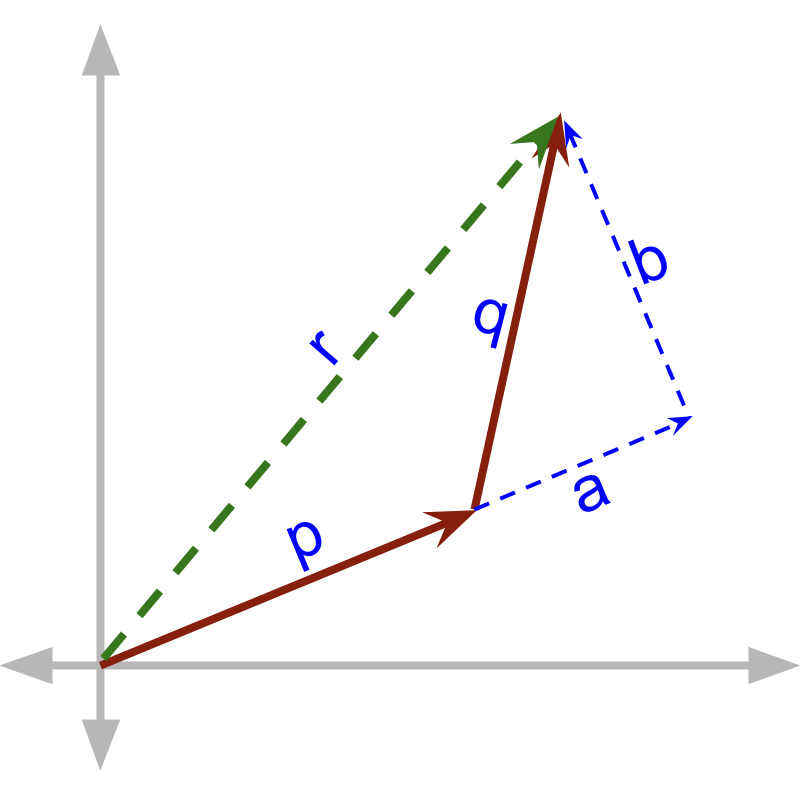    → component in parallel to $\vec{p}$ $vec p$ is $\vec{a}$ $vec a$
    → component in perpendicuar to $\vec{p}$ $vec p$ is $\vec{b}$ $vec b$
    → $\vec{p} + \vec{a}$ $vec p + vec a$ and $\vec{b}$ $vec b$ result in $\vec{r}$ $vec r$

combine

So far, we understood
• vectors are quantities with magnitude and direction
• vectors are represented in the a form that includes the direction, eg: component form $a i + b j + c k$ $ai+bj+ck$

An example of vector quantity is $3$ $3$ meter north, which specifies magnitude $3$ $3$ and direction 'north'.

A person walks $3$ $3$ meter north and continues in the same direction for another $4$ $4$ meter. Since the person walks towards north all the time, the sum is ' $3 + 4$ $3+4$ '.
Two vector quantities add up in magnitude if they are in same direction.

A person walks $3$ $3$ meter north and continues towards east for another $4$ $4$ meter. Since the person walks in different directions, the sum: ' $\neq 3 + 4$ $!=3+4$ '. Two vector quantities do not add up in magnitude if they are not in same direction. The result vector magnitude will be smaller to the direct sum of magnitudes of the vectors.

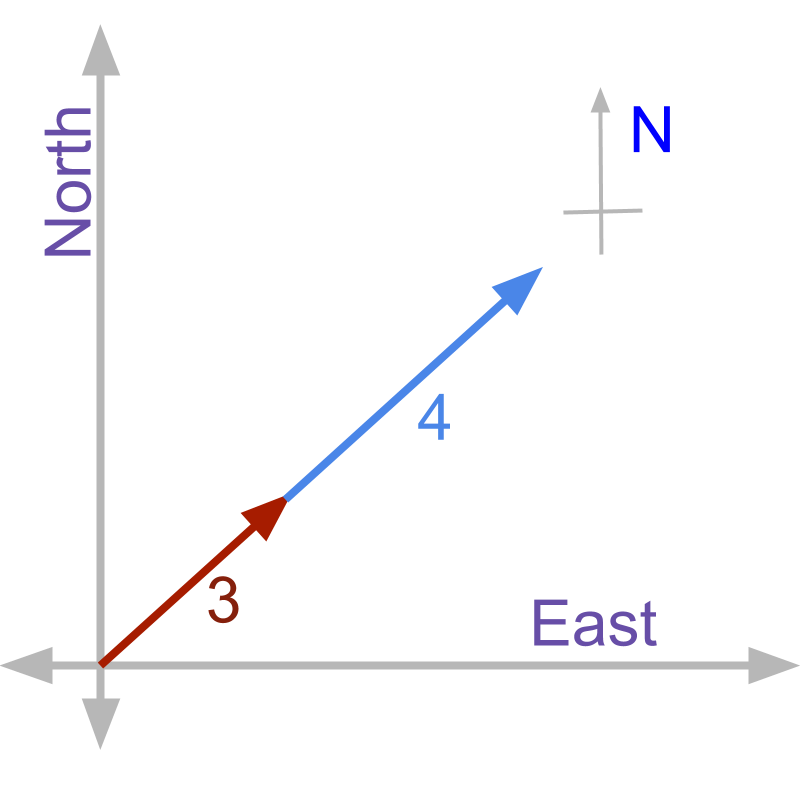
A person walks 3 meter north-east and continues to walk in north-east direction for another 4 meter. Since the person walks in only one direction, the answer is ' $3 + 4$ $3+4$ '. Two vector quantities add up in magnitude if they are in same direction.

A person walks $3$ $3$ meter north-east. He then turns back towards the starting point and walks $2$ $2$ meter towards starting point. The second stretch of walk is considered to be $- 2$ $-2$ in the same direction as the first stretch. One vector subtract from the another vector in magnitude if they are in opposite directions.

abstraction of vector addition

A vector of length $2$ $2$ unit at angle $24^{\circ}$ $24^@$ is added with another vector of $2.3$ $2.3$ unit at angle $24^{\circ}$ $24^@$ . The resulting vector is ' $4.3$ $4.3$ unit at angle $24^{\circ}$ $24^@$ '. Since the direction is same, the vectors add up in magnitude.

A vector of length $1$ $1$ unit at angle $24^{\circ}$ $24^@$ is followed by another vector of $2.3$ $2.3$ unit at angle $43^{\circ}$ $43^@$ . The resulting vector has a magnitude less than 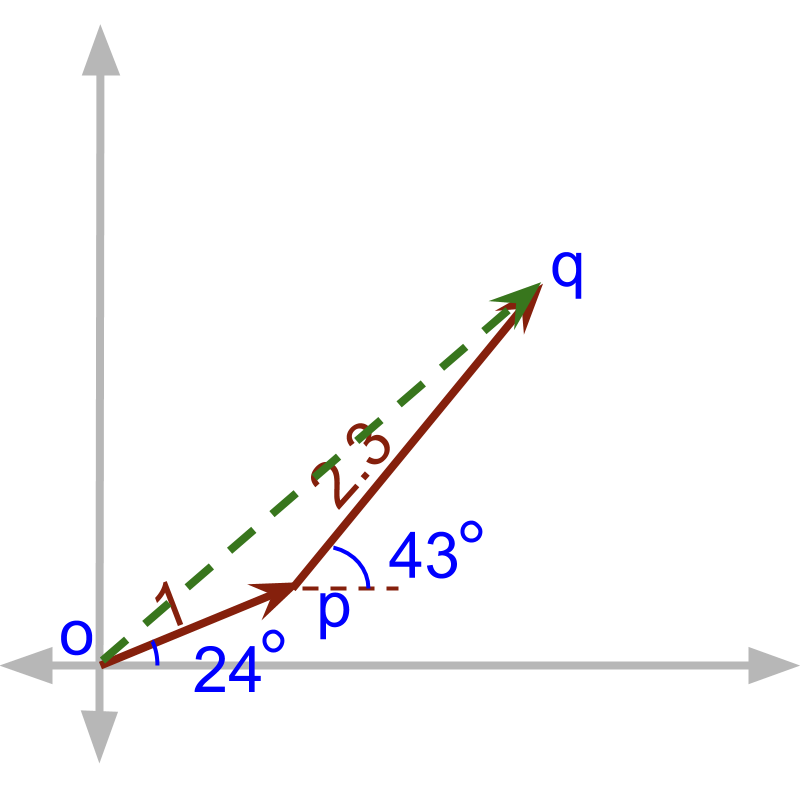$1 + 2.3$ $1+2.3$ '. vector addition first principles The problem is illustrated in figure. The vector of length $1$ $1$ unit at angle $24^{\circ}$ $24^@$ is shown as $\vec{o p}$ $vec(op)$ The vector of $2.3$ $2.3$ unit at angle $43^{\circ}$ $43^@$ is shown as $\vec{p q}$ $vec(pq)$ . The resulting vector of $\vec{o p} + \vec{p q}$ $vec(op) + vec(pq)$ is $\vec{o q}$ $vec(oq)$ . Trigonometrical calculations help in solving this problem.

equivalance in coordinate plane

If the vector in the question represents one of
• force
• electric field
• velocity or
• displacement

. And we have a coordinate geometry representation of lines in the figure. Is that correct to represent the vector quantities as directed line segments? Yes. 'all forms of vectors can be equivalently represented in coordinate plane as rays and geometry can be used to solve'.

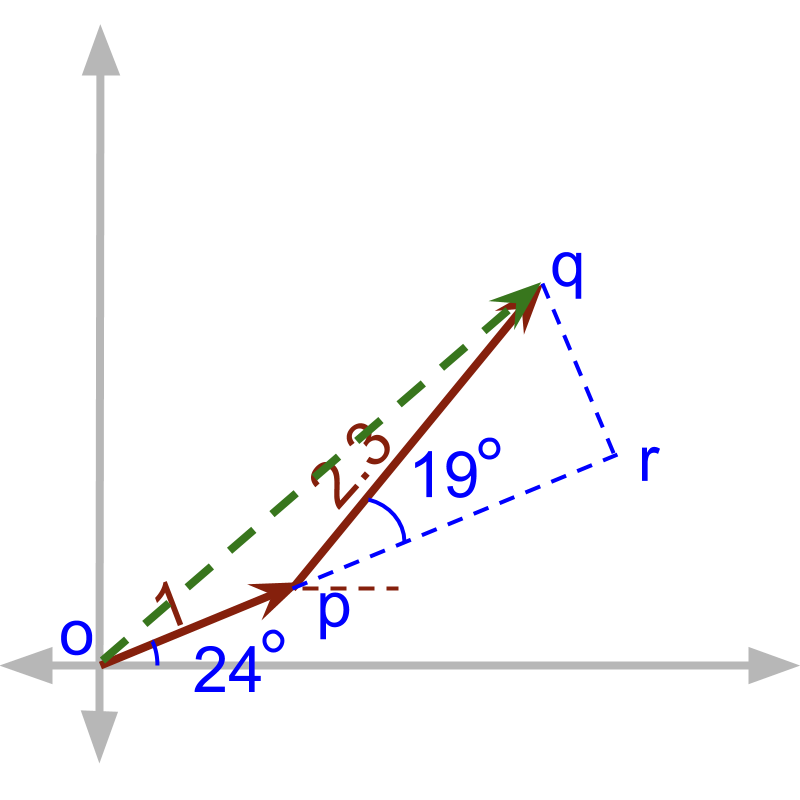
vector addition using trigonometric calculations

The addition is carried out equivalently in coordinate plane. The $\vec{p q}$ $vec(pq)$ is split into two vectors $\vec{p r}$ $vec(pr)$ and $\vec{r q}$ $vec(rq)$ . In this, $\vec{p r}$ $vec(pr)$ is parallel to $\vec{o p}$ $vec(op)$ and $\vec{r q}$ $vec(rq)$ is perpendicular to $\vec{o p}$ $vec(op)$ .

Applying trigonometry, we find the following.
The angle $∠ r p q = 43 - 24 = 19^{\circ}$ $/_ rpq = 43-24 = 19^@$
The magnitute $| \vec{p r} | = 2.3 \cos 19$ $|vec(pr)| = 2.3cos19$
The magnitute $| \vec{r q} | = 2.3 \sin 19$ $|vec(rq)| = 2.3sin19$

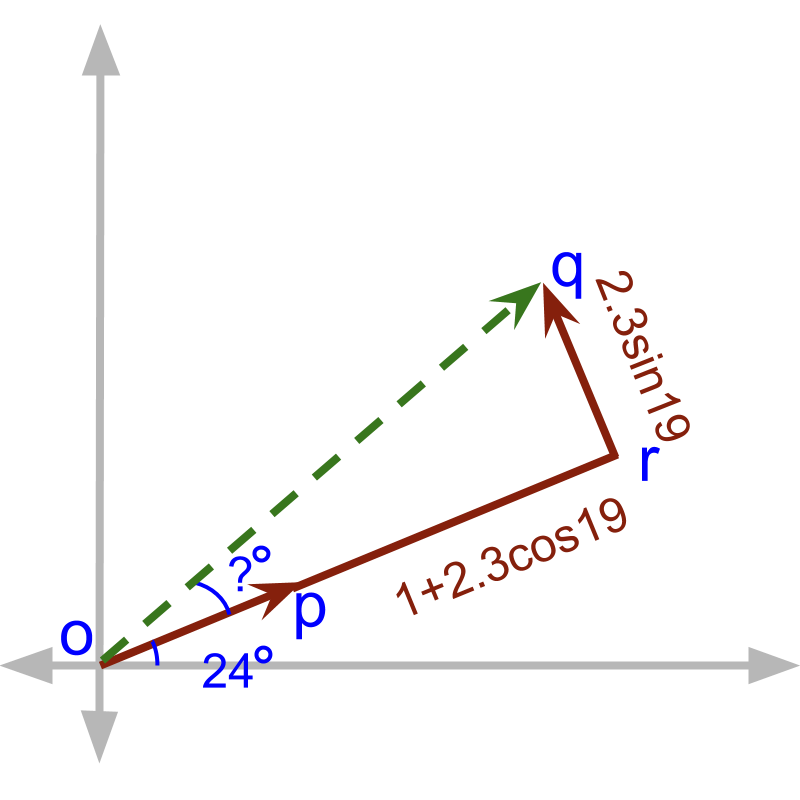vector addition first principles Then, after adding the parallel vectors $\vec{o p} + \vec{p r}$ $vec(op) + vec(pr)$ $= \vec{o r}$ $= vec(o r)$ $= 1 + 2.3 \cos 19$ $= 1+2.3cos19$ . Now to specify the result of addition of two vectors, we need to specify the magnitude $| \vec{o q} |$ $|vec(oq)|$ and angle between $x -$ $x-$ axis and $\vec{o q}$ $vec(oq)$ . We can do simple trigonometric calculation on the triangle $△ o r q$ $/_\ o rq$ .

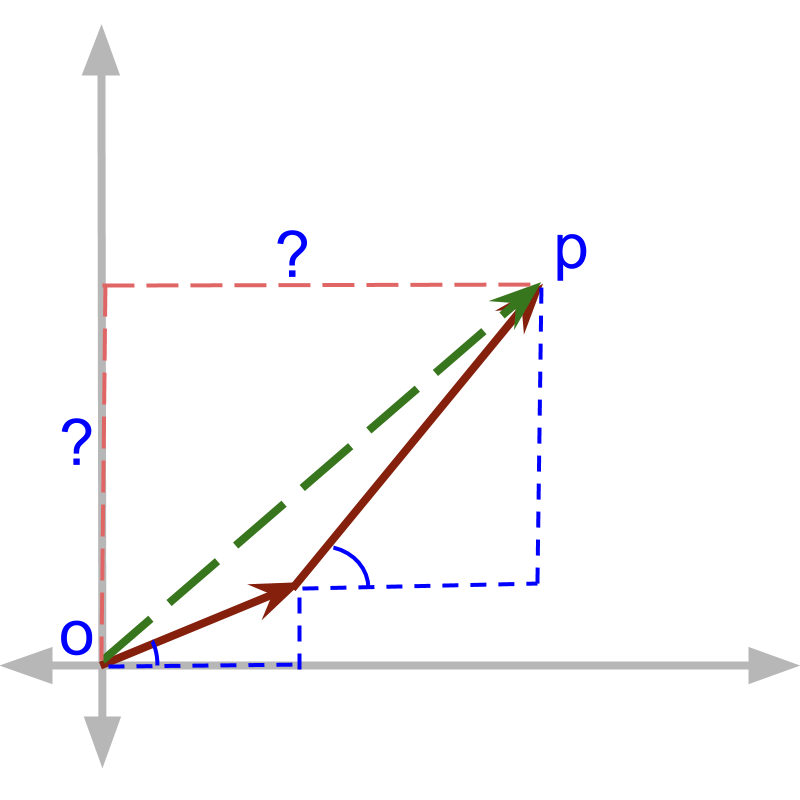
The same can be achieved in a different procedure. The vector of $1$ $1$ unit at $24^{\circ}$ $24^@$ is considered as hypotenuse of right angle triangle. The sides are calculated as ${\cos 24}^{\circ}$ $cos24^@$ and ${\sin 24}^{\circ}$ $sin24^@$ . The same for the vector $2.3$ $2.3$ unit at angle $43^{\circ}$ $43^@$ , the sides are calculated as $2.3 {\cos 43}^{\circ}$ $2.3cos43^@$ and $2.3 {\sin 43}^{\circ}$ $2.3sin43^@$ . This two can be used to find the sides for the result $\vec{O P}$ $vec(OP)$ .

$\vec{O P}$ $vec(OP)$ $= ({\cos 24}^{\circ} + 2.3 \cos 43 \circ) i$ $= (cos24^@+2.3cos43@)i$ $+ ({\sin 24}^{\circ} + 2.3 {\sin 43}^{\circ}) j$ $+(sin24^@+2.3sin43^@)j$ ' as evident from the figure. This is what we follow in general.

Summary:
If two vectors are added, then the result of addition is to be computed using trigonometrical calculations.

If the quantities have the same direction, then the trigonometrical calculations are simple enough that their magnitudes add up.

If the quantities have directions at right angle, then Pythagoras theorem can be used to combine the magnitudes.

If the quantities have different directions, then trigonometric calculations are used to find components in parallel and in perpendicular.

When vectors are added,
• the components in parallel (in the same direction) are directly added in magnitude and
• the components in perpendicular are combined using Pythagoras theorem.

summary

Vector Addition First Principles: When two vectors $\vec{p}$ $vec p$ and $\vec{q}$ $vec q$ are added, vector $\vec{q}$ $vec q$ is split into

• component $\vec{a}$ $vec a$ in parallel to $\vec{p}$ $vec p$ and

• component $\vec{b}$ $vec b$ in perpendicular to $\vec{p}$ $vec p$

$\vec{a}$ $vec a$ is combined to the $\vec{p}$ $vec p$ and $\vec{b}$ $vec b$ is combined using trigonometry.

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed