Vector Algebra : Introduction to Cross Product

maths > vector-algebra

Introduction to Cross Product

what you'll learn...

Overview

Multiplication of Vectors

» Two products because of orthogonality of components of vectors
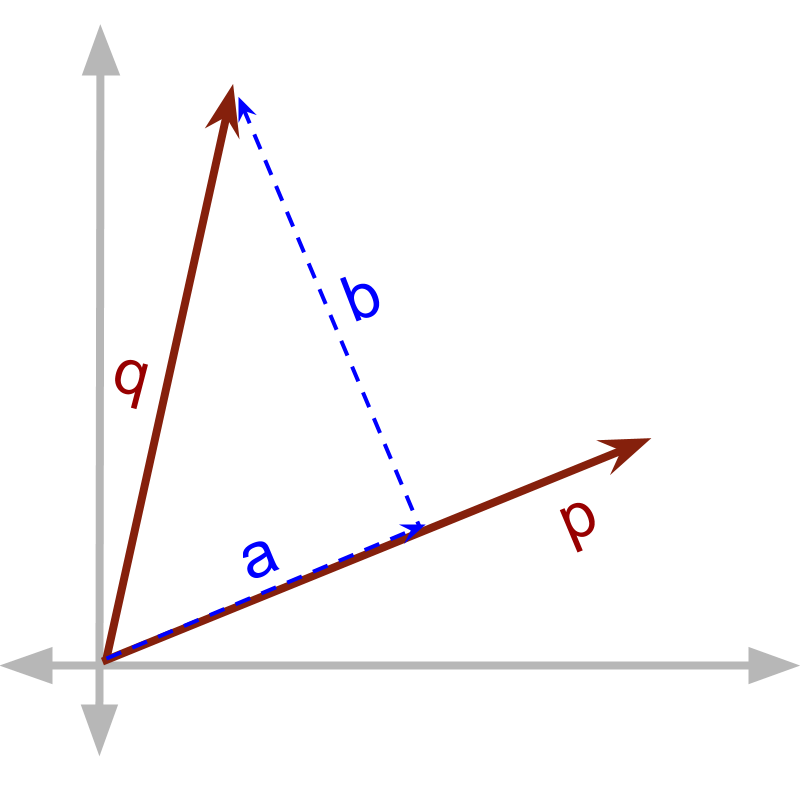→ dot product is defined for components in parallel $\vec{p} \cdot \vec{q}$ $vec p cdot vec q$ $= \vec{p} \cdot \vec{a}$ $=vec p cdot vec a$
→ cross product is defined for components in perpendicular $\vec{p} \times \vec{q}$ $vec p xx vec q$ $= \vec{p} \times \vec{b}$ $=vec p xx vec b$

two products

We have learned that Vector dot product is defined as multiplication of components in parallel. This definition provides mathematical model for the cause and effect which are in the same direction.

In this page, vector cross product is introduced step-by-step.

Direction Property of Cause-Effect relations : When a vector quantity $\vec{x}$ $vec x$ results in another vector quantity $\vec{y}$ $vec y$ ,

(1) in some application scenarios the direction of the result $\vec{y}$ $vec y$ will be same as that of the cause $\vec{x}$ $vec x$ or

(2) in some other application scenarios the direction of the result $\vec{y}$ $vec y$ will be perpendicular to the cause $\vec{x}$ $vec x$ . This property leads to the definition of vector dot product (in which only the parallel components interact) and vector cross product (in which only the perpendicular components interact)

Effect of direction : In mathematical calculations, vectors have the following properties

• A vector is represented as components along orthogonal directions.

• In vector addition, components in parallel add up.

• Two types of vector multiplication are defined for component in parallel and component in perpendicular.

The vector components in parallel form a product named as vector dot product. Vector dot product has meaning or practical application -- cause and effect are in parallel.

Similar to that, does vector cross product has any meaning or practical application? OR is that just an abstraction?
Consider the field of standing crops and a blade is cutting the crop at an angle. Cross product (in which components in perpendicular interact) can be understood with the following

• If the blade runs at right angle to the crop, then it cuts maximum

• If the blade cuts vertically in parallel to the crop, it does not cut any crop

• If the blade cuts at an angle $θ$ $theta$ , then the crop cut is in proportion to the component in perpendicular to the crop

And, of course, the cross product is also used in the abstract form to compute products between vectors.

When two vector quantities interact to form a product, either one of the (1) component in parallel or (2) component in perpendicular is involved in the multiplication.

In practical scenarios, when one component interacts, the other component does not interact and is lost in the product.

summary

At an abstract level, there are two products possible. Given multiplicand $\vec{p}$ $vec p$ and multiplier $\vec{q}$ $vec q$ . $\vec{q}$ $vec q$ is split into $\vec{a}$ $vec a$ and $\vec{b}$ $vec b$ , such that
   $\vec{q} = \vec{a} + \vec{b}$ $vec q = vec a + vec b$ and
   $\vec{a}$ $vec a$ is in parallel to $\vec{p}$ $vec p$
   $\vec{b}$ $vec b$ is in perpendicular to $\vec{p}$ $vec p$

two forms of multiplications are defined for each of these two components.

• one with component in parallel to the other, called vector dot product. $\vec{p} \cdot \vec{q} = \vec{p} \cdot \vec{a}$ $vec p cdot vec q = vec p cdot vec a$

• another with component in perpendicular to the vector, called vector cross product. $\vec{p} \times \vec{q} = \vec{p} \times \vec{b}$ $vec p times vec q = vec p times vec b$

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed