Vector Algebra : Magnitude of a Vector

maths > vector-algebra

Magnitude of a Vector

what you'll learn...

Overview

Magnitude of a Vector

» magnitude of $\vec{p} = a i + b j + c k$ $vec(p) = ai+bj+ck$ is $| \vec{p} | = \sqrt{a^{2} + b^{2} + c^{2}}$ $|vec(p)|= sqrt(a^2+b^2+c^2)$
→ length of $\bar{O P}$ $bar(OP)$ is the magnitude

length of vector

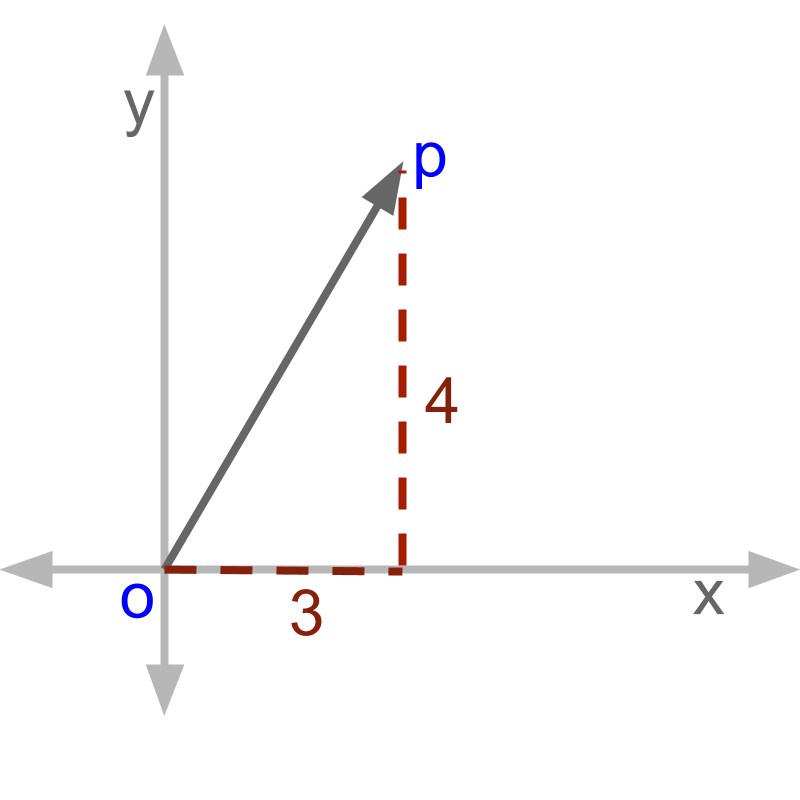
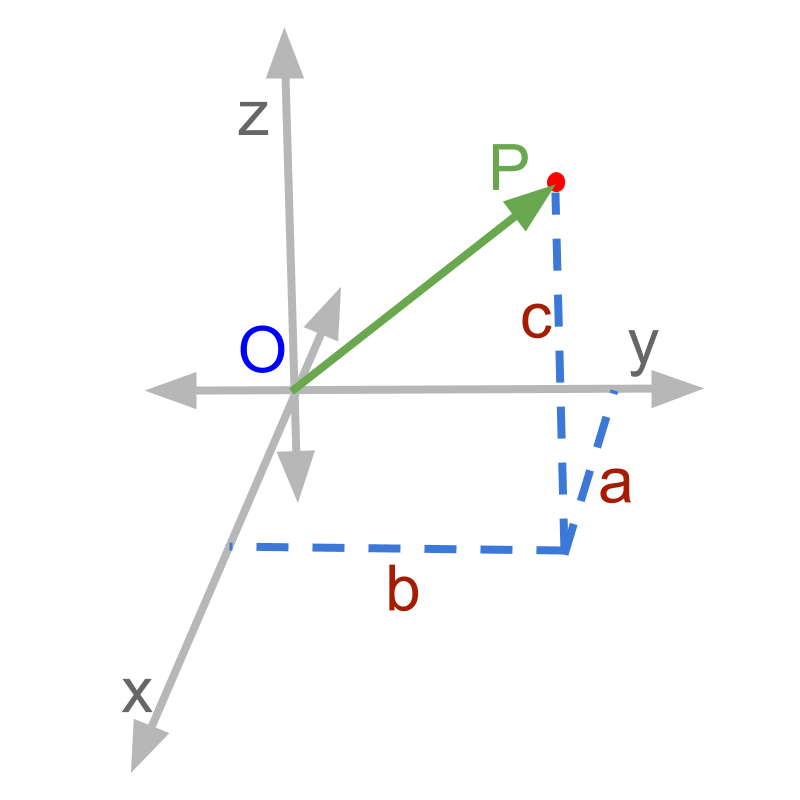
The length of the $\vec{O P}$ $vec(OP)$ in the figure is ' $\sqrt{3^{2} + 4^{2}}$ $sqrt(3^2+4^2)$ ', which is computed using the formula to find hypotenuse of right angled triangles (Pythagoras theorem).

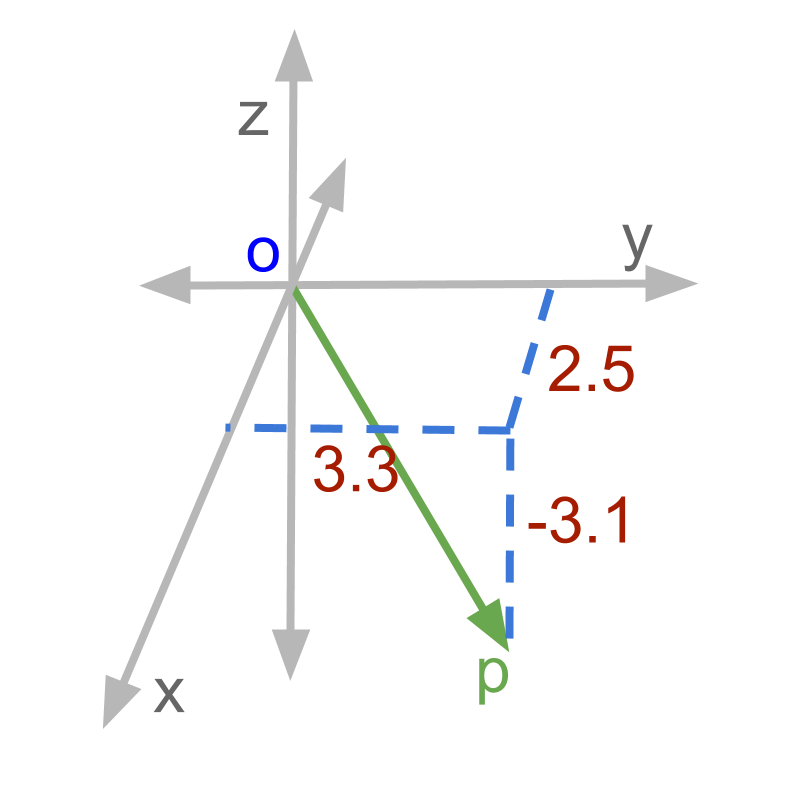
The length of the $\vec{O P}$ $vec(OP)$ in the figure is ' $\sqrt{{3.3}^{2} + {2.5}^{2} + {(- 3.1)}^{2}}'$ $sqrt(3.3^2+2.5^2+(-3.1)^2)'$ .

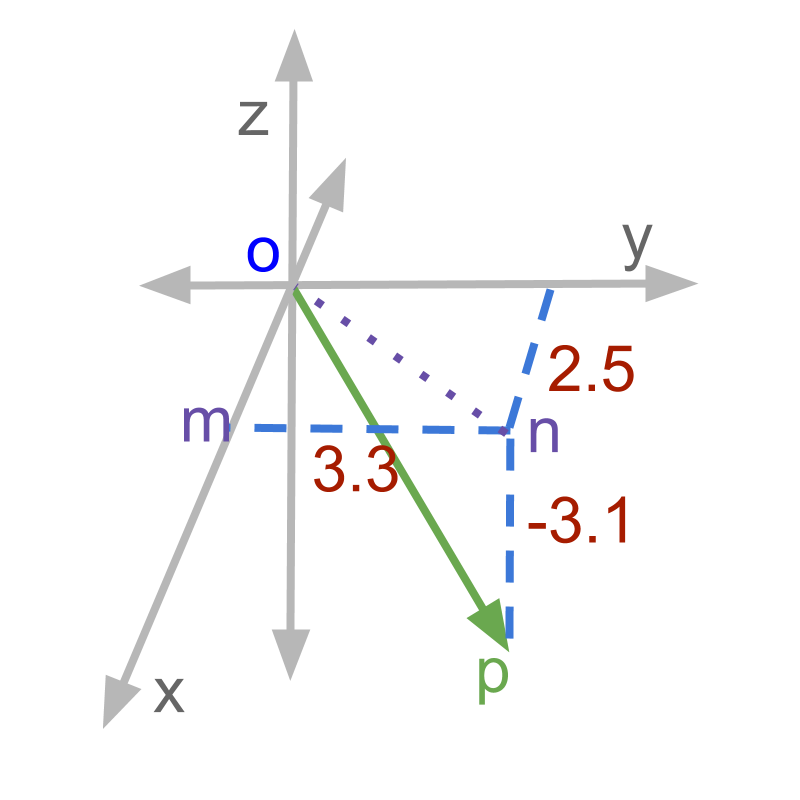
The steps to find length of the vector $\vec{O} P$ $vec OP$ are

• length of $\bar{O N}$ $bar(ON)$ is calculated using $\bar{O M}$ $bar(OM)$ and $\bar{M N}$ $bar(MN)$ as sides of a right angled triangle $O M N$ $OMN$

• length of $\bar{O P}$ $bar(OP)$ is calculated using $\bar{O N}$ $bar(ON)$ and $\bar{N P}$ $bar(NP)$ as sides of a right angled triangle $O N P$ $ONP$

This uses Pythagoras Theorem in two steps.

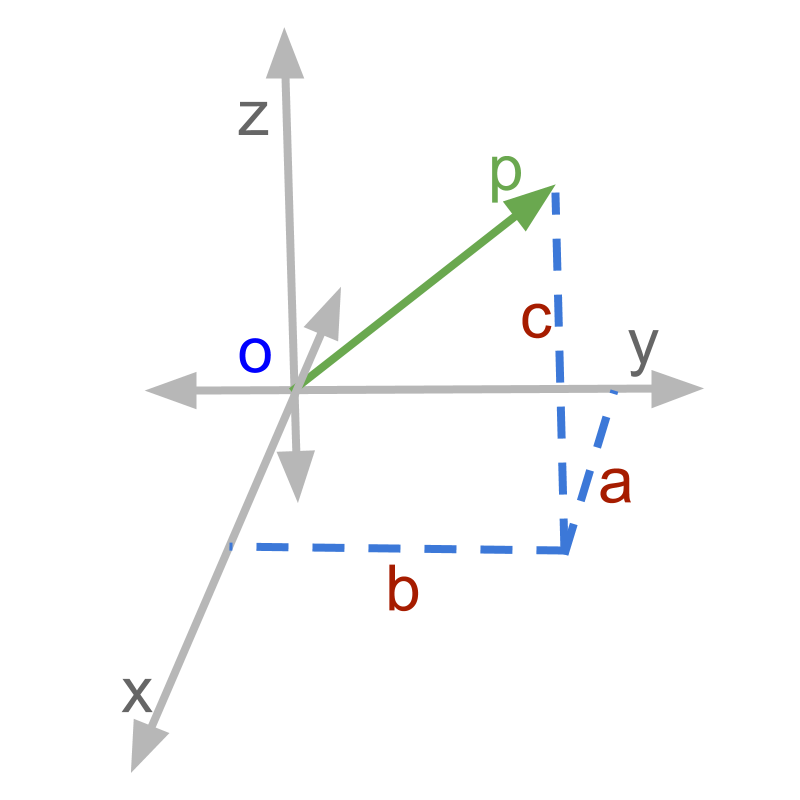
A vector is defined as a quantity with magnitude and direction. If the direction information in removed, the magnitude of a vector is obtained. In this example, length of $\bar{O P}$ $bar(OP)$ is the magnitude of the vector. The magnitude of a vector $a i + b j + c k$ $ai+bj+ck$ is given by $\sqrt{a^{2} + b^{2} + c^{2}}$ $sqrt(a^2+b^2+c^2)$

magnitude

Magnitude of a vector is the 'amount' of the quantity without the direction information.

Magnitude of a Vector: For a vector $\vec{p} = a i + b j + c k$ $vec p = ai+bj+ck$ the magnitude is
$| \vec{p} | = \sqrt{a^{2} + b^{2} + c^{2}}$ $|vec p| = sqrt(a^2+b^2+c^2)$

The word 'magnitude' means size of something.

A point P is given by the vector $2 i + 4 j - 2 k$ $2i+4j-2k$ . What is the distance of the point from the origin? The answer is $\sqrt{2^{2} + 4^{2} + {(- 2)}^{2}}$ $sqrt(2^2+4^2+(-2)^2)$

summary

Magnitude of a Vector: For a vector $\vec{p} = a i + b j + c k$ $vec p = ai+bj+ck$ the magnitude is
$| \vec{p} | = \sqrt{a^{2} + b^{2} + c^{2}}$ $|vec p| = sqrt(a^2+b^2+c^2)$

Magnitude is the 'amount' of the quantity without the direction information.

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed