Vector Algebra : Parallelogram Law

maths > vector-algebra

Parallelogram Law

what you'll learn...

Overview

Vector Addition : Parallelogram Law

» continuous addition of $\vec{x}$ $vec x$ and $\vec{y}$ $vec y$
    → $\vec{x} = \vec{a} + \vec{b}$ $vec x = vec a + vec b$

    → $\vec{y} = \vec{p} + \vec{q}$ $vec y = vec p + vec q$

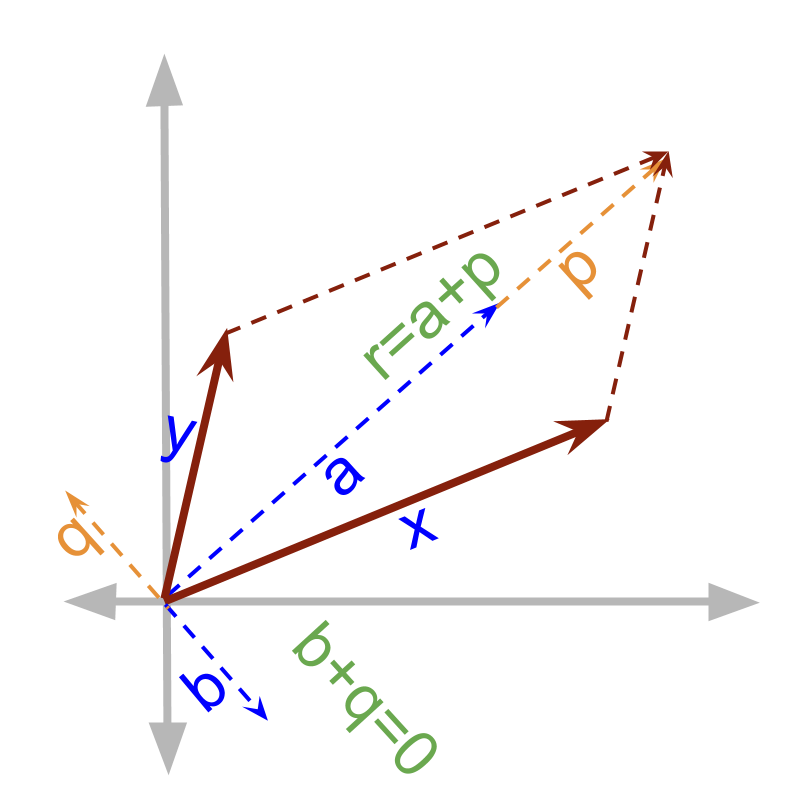    → the co-initial diagonal of the parallelogram formed by sides $\vec{x}$ $vec x$ and $\vec{y}$ $vec y$

continuous addition

Note: Using Geometry, the triangle property of vector addition can be extended to explain parallelogram property of vector addition. In the coming pages, we establish a different point of view for the same.

Two taps simultaneously fill a bucket. One fills at $20$ $20$ liter per hour and another fills at $10$ $10$ liter per hour. This addition is called continuous addition as the quantities are added continuously over time. Scalar quantities can be added continuously..

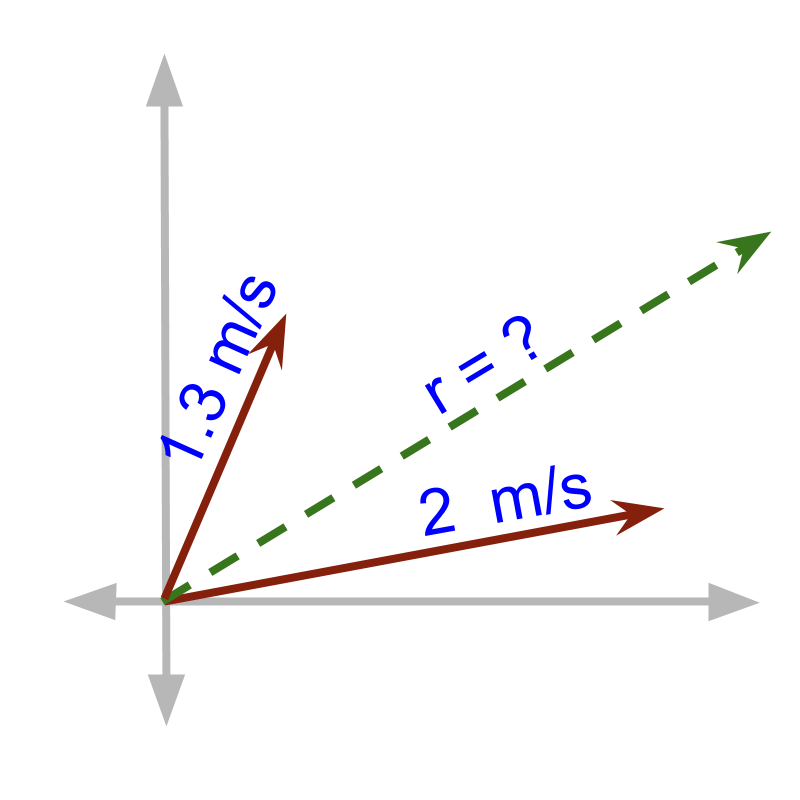
A ball rolls with two velocity components $2$ $2$ m/sec at $11^{\circ}$ $11^@$ angle and $1.3$ $1.3$ m/sec at $67^{\circ}$ $67^@$ angle. The effective velocity of the ball is calculated using Continuous addition of vectors. The two vectors are acting together resulting in a vector sum.

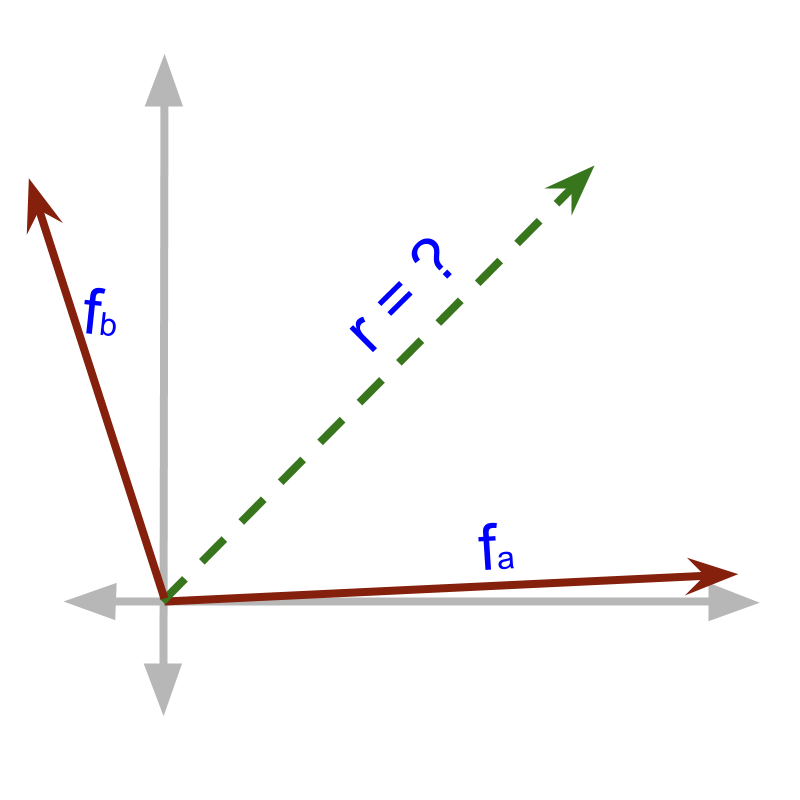
A table is pulled by two persons with forces $f_{a}$ $f_a$ and $f_{b}$ $f_b$ with an angle $θ$ $theta$ between the two forces. The effective force on the table is calculated using Continuous addition of vectors. The two vectors are acting together resulting in a vector sum.

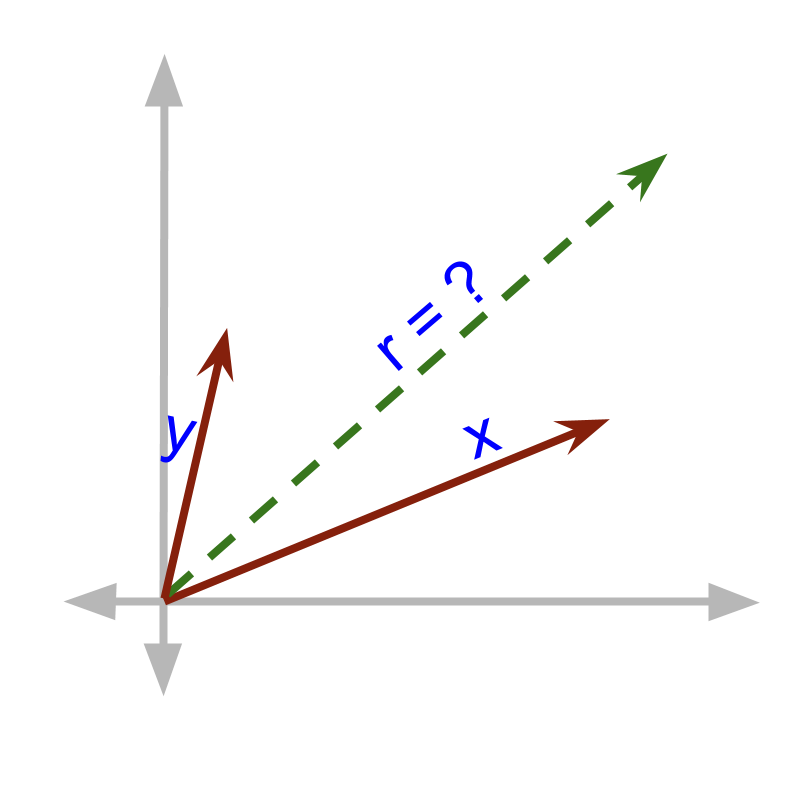
Continuous addition of two vectors is shown in the figure.
The magnitude of a vector is equivalently shown as length of the ray in a coordinate plane. Let us see how to calculate $\vec{r}$ $vec r$ .

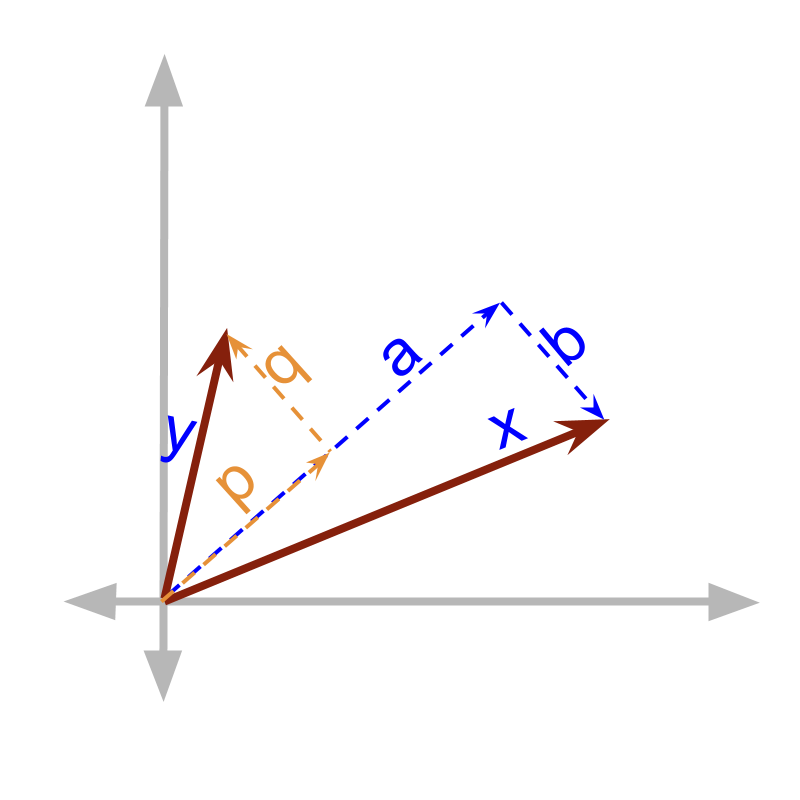
The vectors $\vec{x}$ $vec x$ and $\vec{y}$ $vec y$ can be split into components
• $\vec{x}$ $vec x$ = $\vec{a}$ $vec a$ + $\vec{b}$ $vec b$
• $\vec{y}$ $vec y$ = $\vec{p}$ $vec p$ + $\vec{q}$ $vec q$

Note that $\vec{b}$ $vec b$ = $- \vec{q}$ $-vec q$
and $\vec{a}$ $vec a$ and $\vec{p}$ $vec p$ are in the same direction.

The component vectors are equivalently rearranged as shown in the figure. $\vec{a}$ $vec a$ and $\vec{p}$ $vec p$ add in magnitude, as they are in the same direction.

The component vectors are equivalently rearranged as shown in the figure. $\vec{b}$ $vec b$ and $\vec{q}$ $vec q$ subtract in magnitude and cancel out to $0$ $0$ , as they are in the opposite direction and of same magnitude.

Note that the result forms a diagonal to the parallelogram. This is given as the parallelogram property of vector addition.

Two vectors form a parallelogram and the co-initial diagonal is the sum.

summary

Parallelogram Property of vector addition : when two vectors are added, arrange such that their initial points coincide. In that configuration, complete a parallelogram with the two vectors as the two adjacent sides. The diagonal that starts from the initial point of the vectors is the sum of the two vectors.

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed