Vector Algebra : Position Vector of a Point

maths > vector-algebra

Position Vector of a Point

what you'll learn...

Overview

Position Vector of a Point

» For a point $P (a, b, c)$ $P(a,b,c)$ the position vector is $\vec{O P} = a i + b j + c k$ $vec(OP) = ai+bj+ck$

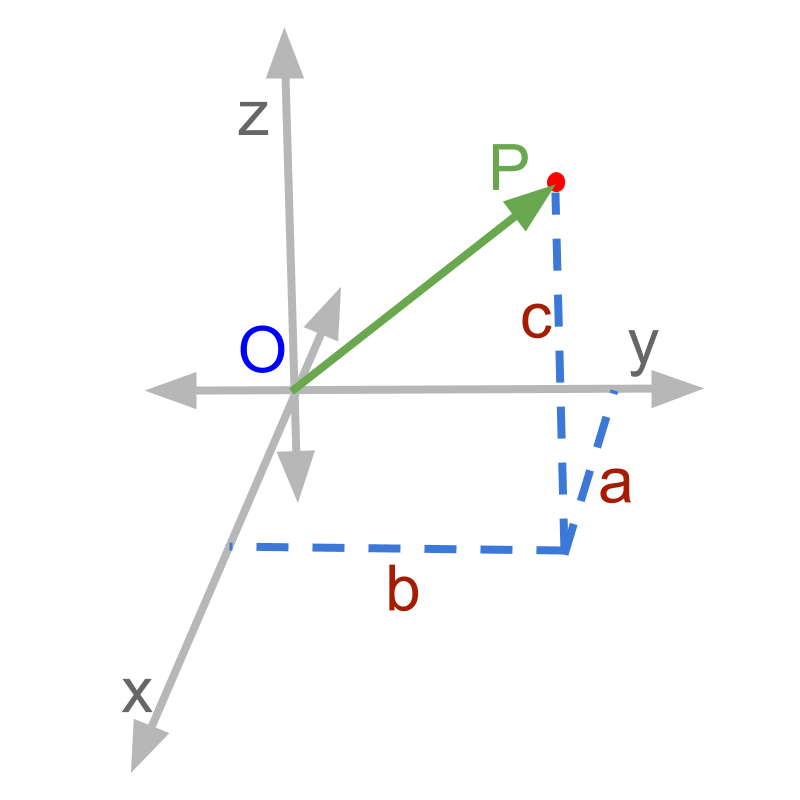
position means place

Consider a point $P$ $P$ in 3D coordinate system as shown in figure. The point $P$ $P$ is given by the following.

   $⋆$ $***$ in 3D coordinates it is $(a, b, c)$ $(a,b,c)$

   $⋆$ $***$ as a vector representation $a i + b j + c k$ $ai+bj+ck$

   $⋆$ $***$ as the vector $\vec{O P}$ $vec(OP)$

The word 'position' means 'place; location'.

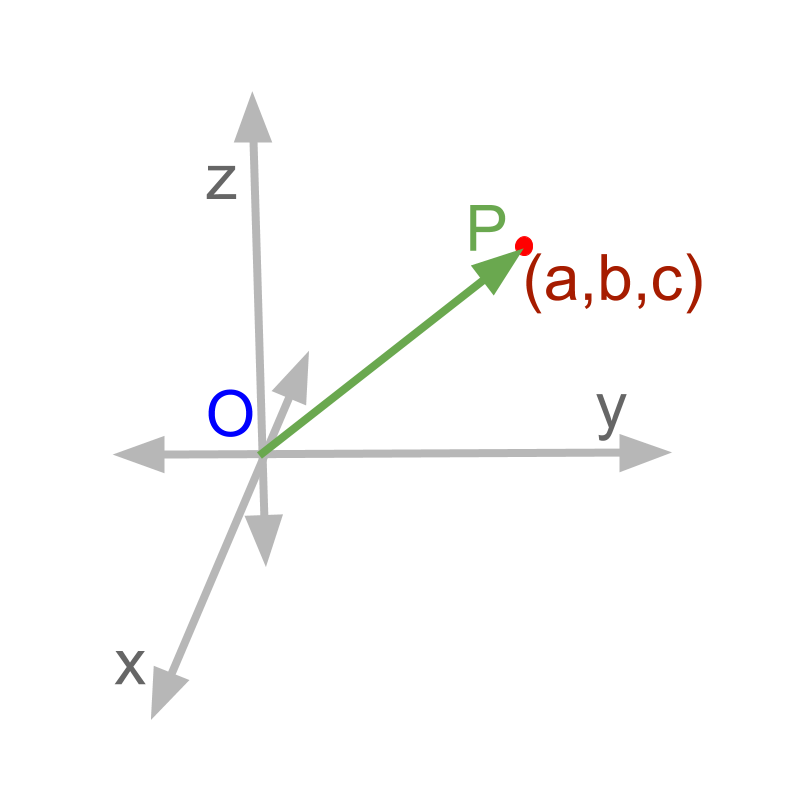
Given a point $P (a, b, c)$ $P (a,b,c)$ as shown in figure. Position vector of a point $P (a, b, c)$ $P (a,b,c)$ is
$\vec{O P} = a i + b j + c k$ $vec(OP)=ai+bj+ck$

Position Vector: For a point $P (a, b, c)$ $P (a,b,c)$ the position vector is
$\vec{O P} = a i + b j + c k$ $vec(OP)=ai+bj+ck$ .

Position Vector of a Point is the vector between origin and the point.

examples

What is the position vector of point $(2, - \frac{3}{4})$ $(2,-3/4)$ ?

The answer is ' $2 i - \frac{3}{4} j$ $2i-3/4j$ '.

Given the vector $\vec{O P} = 3 i - 1.4 j + 2.5 k$ $vec(OP) = 3i-1.4j+2.5k$ , if $O$ $O$ is the origin, what is the coordinate position of point $P$ $P$ ?

The answer is ' $(3, - 1.4, 2.5)$ $(3,-1.4,2.5)$ '

What is the position vector of point $(0, - 2.1, 3.4)$ $(0,-2.1,3.4)$ ?

The answer is ' $- 2.1 j + 3.4 k$ $-2.1j+3.4k$ '.

summary

Position Vector: For a point $P (a, b, c)$ $P (a,b,c)$ the position vector is
$\vec{O P} = a i + b j + c k$ $vec(OP)=ai+bj+ck$ .

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed