Vector Algebra : Mathematical Representation of Vectors

maths > vector-algebra

Mathematical Representation of Vectors

what you'll learn...

Overview

Representation of Vectors

» Specify amount or magnitude and direction

    → $3$ $3$ m east and $4$ $4$ m north

    → $3$ $3$ m east and $4$ $4$ m north-east

» How were the quantities added?

    → $3$ $3$ m east + $4$ $4$ m north = $\sqrt{3^{2} + 4^{2}}$ $sqrt(3^2+4^2)$ as per Pythagoras theorem

    → $3$ $3$ m east + $4$ $4$ m north-east : Making this easy to do is the objective of "vector algebra"

» Position of an airplane $a i + b j + c k$ $ai+bj+ck$

    → 3Okm east (x-axis) = $30 i$ $30i$

    → 40km north (y-axis) = $40 j$ $40j$

    → 4km altitude (z-axis) = 4k

» component form of a vector $a i + b j + c k$ $ai+bj+ck$
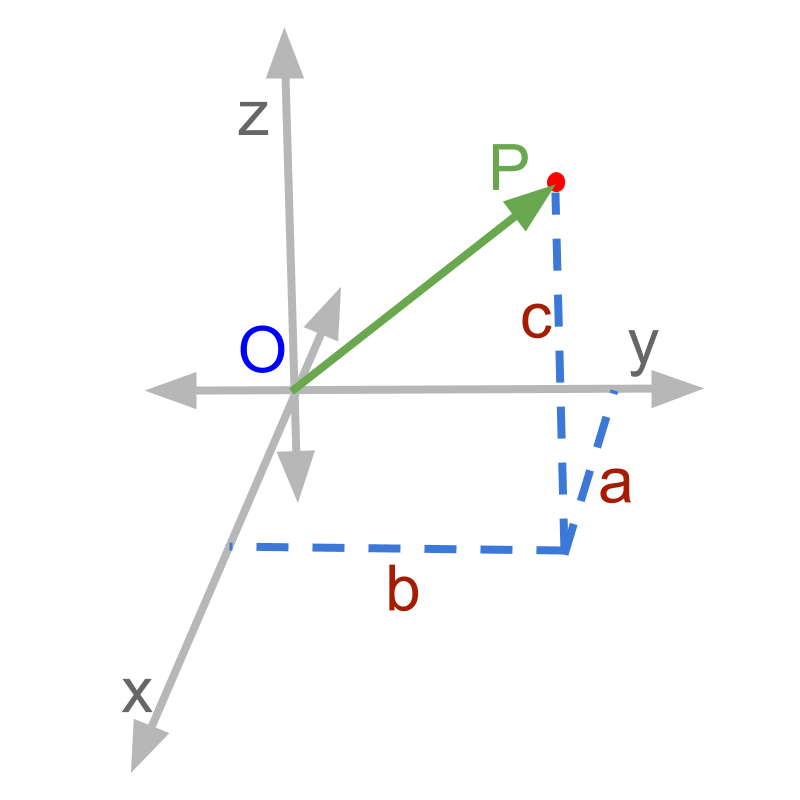vector representation     → $i$ $i$ , $j$ $j$ , $k$ $k$ represent the direction along $x$ $x$ , $y$ $y$ , and $z$ $z$ axes

    → $a$ $a$ , $b$ $b$ , $c$ $c$ represent the amount or magnitude along the given directions

illustrative example

If someone is calculating the position of an airplane, a reasonable specification of the position is

$30$ $30$ km to the east, $40$ $40$ km north, and at $4$ $4$ km altitude above sea level

This specifies - North, East, and Altitude. With these three pieces of information, the position of the airplane is specified clearly.

We have arrived at representing vectors that have magnitude and direction.

The representation is
$30$ $30$ km East + $40$ $40$ km North + $4$ $4$ km Altitude

This can be generalized to a 3D space with three axes x-axis, y-axis, and z-axis. The figure represents x-axis, y-axis, and z-axis. A point 'p' is shown.

The x, y, and z coordinates are given as $(x, y, z)$ $(x,y,z)$ . The point given in figure is ' $(4, 7, 10)$ $(4,7,10)$ '.
The point is projected onto x-y plane. That is further projected onto x and y axes.

The airplane can be considered as the point 'p' in the three dimensional space. The representation is simplified as
$4 i + 7 j + 10 k$ $4i+7j+10k$
or alternatively
$4 \hat{i} + 7 \hat{j} + 10 \hat{k}$ $4 hat i+7 hat j+10 hat k$
Where
$i$ $i$ or $\hat{i}$ $hat i$ represents the direction in $x$ $x$ -axis
$j$ $j$ or $\hat{j}$ $hat j$ represents the direction in $y$ $y$ -axis
$k$ $k$ or $\hat{k}$ $hat k$ represents the direction in $z$ $z$ -axis

Note: $\hat{i}$ $hat i$ is pronounced as i-hat or i-cap.

A 3D vector quantity is represented with 3 components along the three directions of 3D coordinates.

Mathematical representation: A 3D vector quantity is represented in the form $a i + b j + c k$ $ai+bj+ck$
or alternatively
$a \hat{i} + b \hat{j} + c \hat{k}$ $a hat i+b hat j+c hat k$
Where i, j, k are the directions along x, y, and z axes
and a, b, c are the magnitude along the directions respectively.

examples

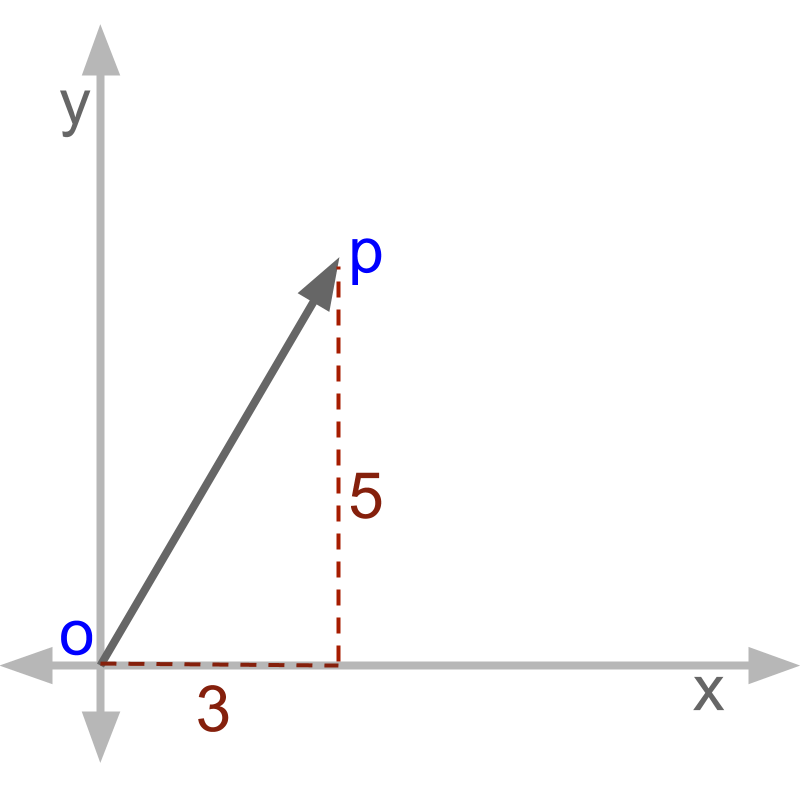
Represent OP as a vector.The answer is ' $3 i + 5 j$ $3i+5j$ '.
The x-axis component is represented with an $i$ $i$ and y-axis component is represented with a $j$ $j$ .

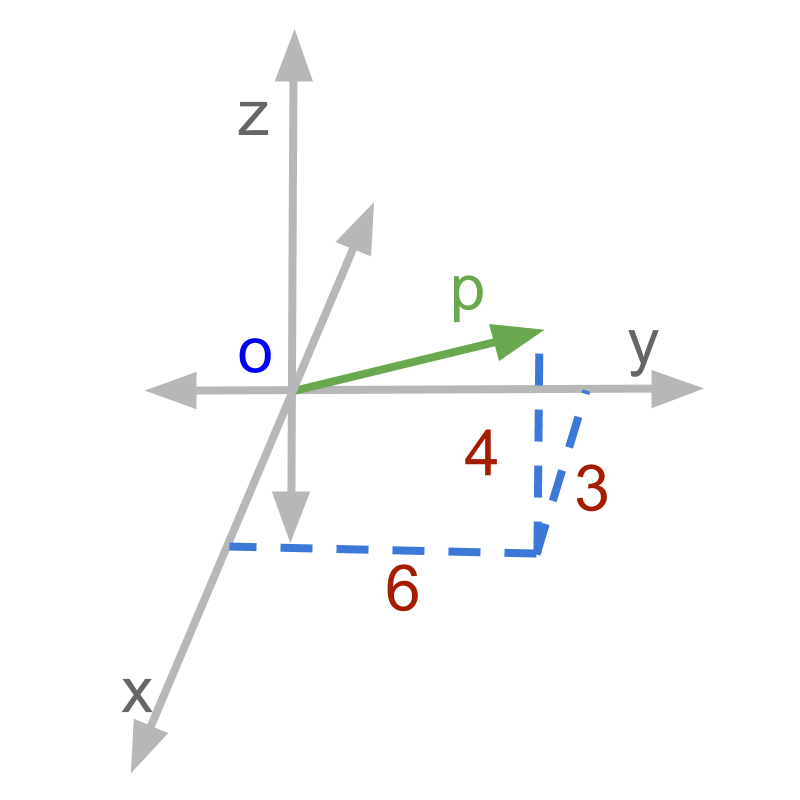
What is the vector form of $\bar{O P}$ $bar(OP)$ ? The answer is ' $3 i + 6 j + 4 k$ $3i+6j+4k$ '. Referring to the figure, the component along each of the axes
$3 i$ $3i$ : $3$ $3$ along x axis
$6 j$ $6j$ : $6$ $6$ along y axis
$4 k$ $4k$ : $4$ $4$ along z axis

What is the vector form of OP? The answer is ' $- 1.3 i - \frac{11}{2} j + 4 k$ $-1.3i-11/2 j+4k$ '.

What is the vector form of OP? $2.4 i + \frac{7}{2} j$ $2.4i+ 7/2 j$ or $2.4 i + \frac{7}{2} j + 0 k$ $2.4i+ 7/2 j+0k$ When a two dimensional vector is presented, the component along the third dimension is 0.

A point is located from the x, y, z-axes at distances $2$ $2$ , $- 1.2$ $-1.2$ , and $1.4$ $1.4$ units respectively. What is the vector representation of the point?

The answer is ' $2 i - 1.2 j + 1.4 k$ $2i-1.2j+1.4k$ '

What does a $\vec{O P} = - .5 i + 2.1 j - .6 k$ $vec(OP) = −.5i+2.1j−.6k$ mean?
the point P is $- 0.5$ $−0.5$ unit away from origin along x-axis
the point P is $2.1$ $2.1$ unit away from origin along y-axis
the point P is $- 0.6$ $−0.6$ unit away from origin along z-axis

summary

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed