Vector Algebra : Vector Dot Product : Projection of a vector

maths > vector-algebra

Vector Dot Product : Projection of a vector

what you'll learn...

Overview

Vector Dot Product: Projection form

» component in parallel is calculated by the angle
    → $\vec{p} \cdot \vec{q}$ $vec p cdot vec q$ $= | \vec{p} | | \vec{q} | \cos θ$ $= |vec p| |vec q| cos theta$
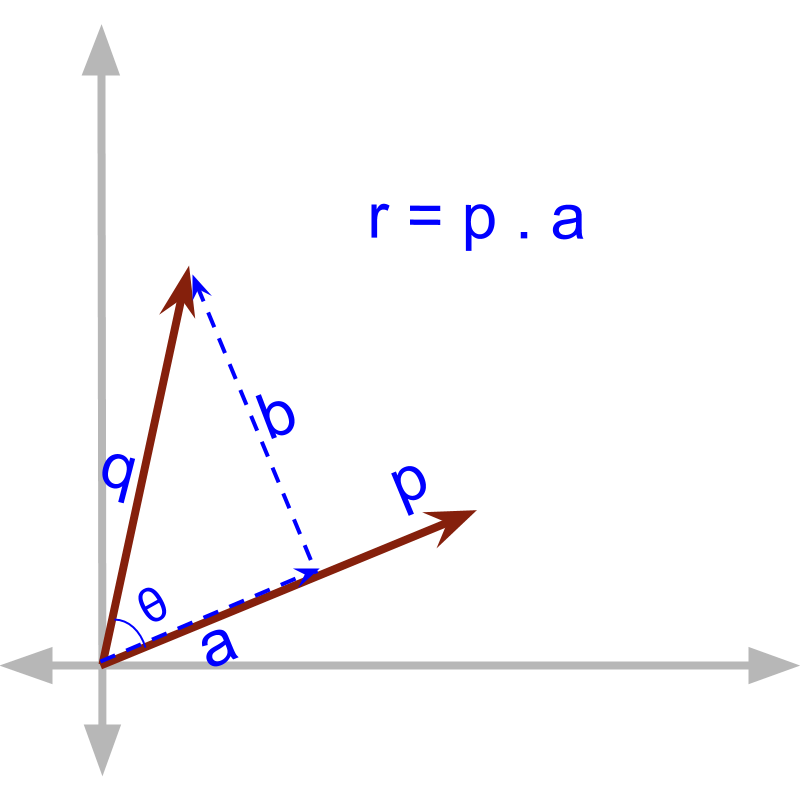    → Note that $| \vec{a} | = | \vec{q} | \cos θ$ $|vec a| = |vec q|cos theta$
    → $\vec{a}$ $vec a$ is the projection of $\vec{q}$ $vec q$ on $\vec{p}$ $vec p$

projection

Vector dot product is understood as product between components in parallel to each other.
In finding the component in parallel to one vector the vector is projected on to another. In the figure, $a$ $a$ is the projection of $\vec{q}$ $vec q$ onto $\vec{p}$ $vec p$

That means $a$ $a$ can be calculated using vector dot product. That is, the vector dot product can be used to find projection of a vector on a line.

Consider the line given by $\vec{s}$ $vec s$ and the vector $\vec{p}$ $vec p$ as shown in the figure. We know that $\vec{s} \cdot \vec{p} = | \vec{s} | | \vec{p} | \cos θ$ $vec s cdot vec p = |vec s| |vec p| cos theta$ .
To find the projection of $\vec{p}$ $vec p$ on $\vec{s}$ $vec s$ , the following can be used

$\hat{s} \cdot \vec{p}$ $hat s cdot vec p$ , where $\hat{s}$ $hat s$ is unit vector

$\frac{\vec{s}}{| \vec{s} |} \cdot \vec{p}$ $(vec s)/(|vec s|) cdot vec p$

Two vectors $\vec{p}$ $vec p$ and $\vec{q}$ $vec q$ with magnitudes $2$ $2$ and $3$ $3$ respectively are at an angle $60^{\circ}$ $60^@$ . What is the projection of $\vec{p}$ $vec p$ on $\vec{q}$ $vec q$ ?

The answer is 'All the above'.

summary

Projection of a vector: Projection of a vector $\vec{p}$ $vec p$ on a line in direction $\vec{s}$ $vec s$ is
$= \vec{p} \cdot \hat{s}$ $= vec p cdot hat s$
where $\hat{s}$ $hat s$ is the unit vector along $\vec{s}$ $vec s$ .

Vector dot product can be used to find projection of a vector on a line or on another vector.

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed