Vector Algebra : Cause-Effect relation

maths > vector-algebra

Cause-Effect relation

what you'll learn...

Overview

cause-effect relations

» Two vectors that are cause-effect relation will be in same direction
    → $\vec{x}$ $vec x$ is the cause
    → $\vec{y}$ $vec y$ is the effect of the cause
    → both $\vec{x}$ $vec x$ and $\vec{y}$ $vec y$ will be in same direction

» Dot product is defined for applications with product involving cause-effect relation

» Note: the dot product is used in applications where parallel components take part in multiplication

relation

In this chapter, the product defined for components in parallel is discussed. First, let us establish the application scenario where components in parallel interact to form a product.

A pen can be used to write $30$ $30$ pages. With $4$ $4$ pens, one can write $4 \times 30 = 120$ $4xx30 = 120$ pages. Increase in the number of pen causes increase in the number of pages, which is the effect of the cause.

In this "number of pen" is a cause and "number of pages" is an effect.

This is an example of cause and effect relation in scalar quantities.

Some cause-effect relations are

• Volume of Paint and painted area

• Number of tickets sold and the money collected in the sale

• speed of a car and distance covered in an hour

Similar to the cause-effect relations of scalar quantities, vectors have cause and effect relations.

2 liter of paint is required to paint 3 square meter. If 14 liter paint is available, how much area can be painted?

The answer is " $14 \times \frac{3}{2}$ $14 xx 3/2$ "

• The "volume of paint" is the cause.

• The "area painted" is the effect.

• This cause-effect relation is defined by a function involving multiplication by a constant.
$area = volume \times \frac{3}{2}$ $text(area) = text(volume) xx 3/2$ .

Everyday, a hotel sends a worker to buy eggs from market. The eggs are priced at $1$ $1$ coin each and the worker charges $5$ $5$ coins for the travel to buy eggs. How many coins are to be given to buy $120$ $120$ eggs?

The answer is " $125$ $125$ coins".

• The "number of eggs" is the cause.

• The "coins" is the effect.

• This cause-effect relation is defined by a function involving addition of a constant.
$coins =$ $text(coins) =$ $number of eggs$ $text(number of eggs)$ $\times price per egg$ $xx text( price per egg)$ $+ 5$ $+ 5$

From the examples, it is understood that, Definition of a relation as an expression involves

• addition and subtraction

• multiplication and division

• exponents and roots

Apart from these arithmetic operations, quantities may be related by

• rate of change, which is covered in differential calculus

• aggregate which is covered in integral calculus

The quatities involved need not be scalars, one or both of the quantities may be vectors.

An example of cause-effect relation in vector quantities is 'pull a table and the table moves'. Pulling force has direction and the movement of the table has direction. So, Both of them are vector quantities.

Examples of cause-effect relations in vector quantities

• velocity and displacement

• acceleration and velocity

• force and acceleration

• force and displacement

• force and velocity

• acceleration and displacement

Two vector quantities may be connected with cause-effect relation.

One pulls a table towards east direction. Then the table will move towards east.

Is it possible that the table move in any direction other than the direction of force? (given that no other force is acting on the table.) 'No, Not possible'.

If the force is in one direction, then the displacement due to that force is in the same direction.

A ball moves with velocity $\vec{v}$ $vec v$ . The displacement due to that velocity be 'in the same direction as $\vec{v}$ $vec v$ '.

A ball moves with velocity ${\vec{v}}_{1}$ $vec v_1$ in one direction and velocity ${\vec{v}}_{2}$ $vec v_2$ in another direction. The sum of velocities $\vec{v} = {\vec{v}}_{1} + {\vec{v}}_{2}$ $vec v = vec v_1 + vec v_2$ .

• The displacement ${\vec{s}}_{1}$ $vec s_1$ due to ${\vec{v}}_{1}$ $vec v_1$ will be in the direction of ${\vec{v}}_{1}$ $vec v_1$ '.

• The displacement ${\vec{s}}_{2}$ $vec s_2$ due to ${\vec{v}}_{2}$ $vec v_2$ will be in the direction of ${\vec{v}}_{2}$ $vec v_2$ '.

• The total some displacement $\vec{s}$ $vec s$ due to $\vec{v}$ $vec v$ will be in the direction of $\vec{v}$ $vec v$ , and also that $\vec{s} = {\vec{s}}_{1} + {\vec{s}}_{2}$ $vec s = vec s_1 + vec s_2$ .

Note that the displacement component is in the same direction as the velocity component causing it.
• ${\vec{s}}_{1}$ $vec s_1$ is in the direction of ${\vec{v}}_{1}$ $vec v_1$
• ${\vec{s}}_{2}$ $vec s_2$ is in the direction of ${\vec{v}}_{2}$ $vec v_2$
• ${\vec{s}}_{1} + {\vec{s}}_{2}$ $vec s_1+vec s_2$ is in the direction of ${\vec{v}}_{1} + {\vec{v}}_{2}$ $vec v_1+vec v_2$

The above is an example of cause and effect being in the same direction. Due to orthogonality of directions, either one of the following is true for an application scenario.
• The cause and effect are parallel. OR
• The cause and effect are in perpendicular.

Direction Property of Cause-Effect relations : When a vector quantity $\vec{x}$ $vec x$ results in another vector quantity $\vec{y}$ $vec y$ ,

(1) in some application scenarios the direction of the result $\vec{y}$ $vec y$ will be same as that of the cause $\vec{x}$ $vec x$ or

(2) in some other application scenarios the direction of the result $\vec{y}$ $vec y$ will be perpendicular to the cause $\vec{x}$ $vec x$ . This property leads to the definition of vector dot product (in which only the parallel components interact) and vector cross product (in which only the perpendicular components interact)

One pulls a table towards east and at the same time, another pulls the same table towards north. If both are pulling with same magnitude, then the table will move in 'North-East' direction.
This can be verified with a simple experiment at home / class.

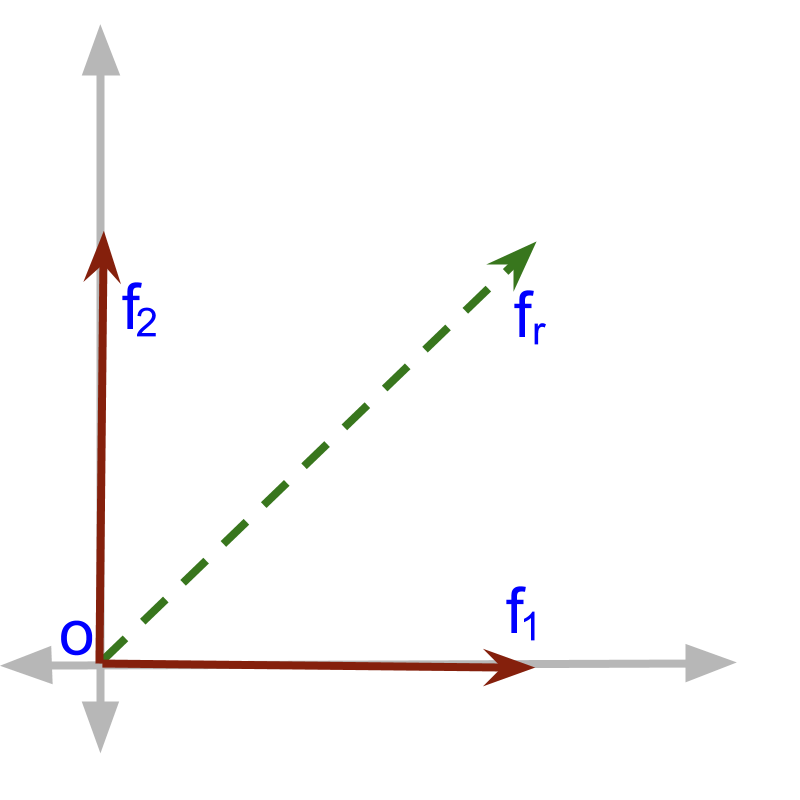
The problem is shown in the figure. The forces ${\vec{f}}_{1}$ $vec f_1$ and ${\vec{f}}_{2}$ $vec f_2$ . The combined ${\vec{f}}_{r}$ $vec f_r$ is shown. ${\vec{f}}_{r} = {\vec{f}}_{1} + {\vec{f}}_{2}$ $vec f_r = vec f_1+vec f_2$ . Parallelogram law of Vector Addition or Triangular law of Vector Addition can be used interchangeably to solve this. Triangular law or Parallelogram law are to understand different aspects of vector addition, and both equivalently describe vector addition.

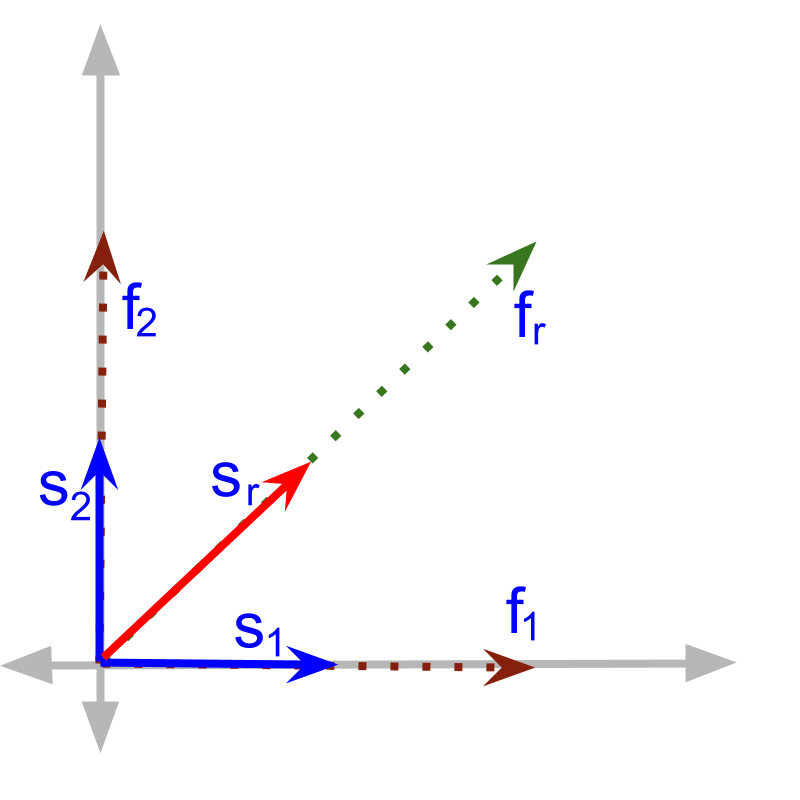
The displacement $\vec{s}$ $vec s$ , due to force $\vec{f}$ $vec f$ , is shown in the figure. The following is understood from the figure
• ${\vec{f}}_{1}$ $vec f_1$ causes ${\vec{s}}_{1}$ $vec s_1$ in the same direction
• ${\vec{f}}_{2}$ $vec f_2$ causes ${\vec{s}}_{2}$ $vec s_2$ in the same direction
• ${\vec{f}}_{r}$ $vec f_r$ causes ${\vec{s}}_{r}$ $vec s_r$ in the same direction

If force $\vec{f}$ $vec f$ causes $\vec{s}$ $vec s$ displacement, then the work done by the force is calculated as
work = $f$ $f$ multiplied by $s$ $s$

Given the force, displacement pairs in the figure, the work done by force ${\vec{f}}_{r}$ $vec f_r$ is ' $f_{r}$ $f_r$ multiplied by $s_{r}$ $s_r$ '. Because $f_{r}$ $f_r$ causes $s_{r}$ $s_r$ .

Given the force, displacement pairs in the figure, the work done by force ${\vec{f}}_{1}$ $vec f_1$ is ' $f_{1}$ $f_1$ multiplied by $s_{1}$ $s_1$ '. Because $f_{1}$ $f_1$ causes $s_{1}$ $s_1$ .

summary

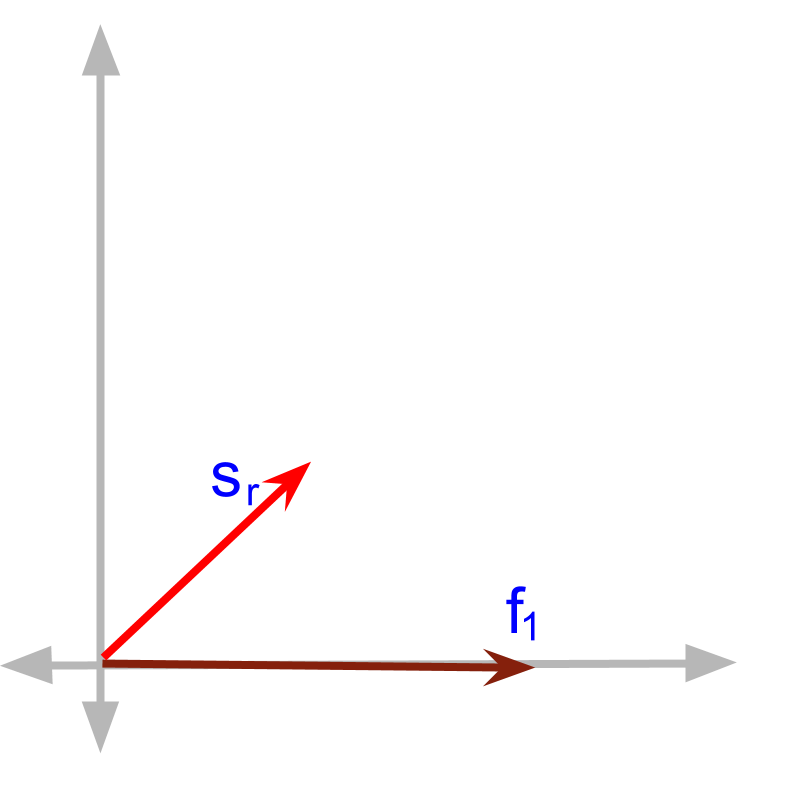
The force and displacement pair are given as in the figure. Note that only force ${\vec{f}}_{1}$ $vec f_1$ and displacement $s_{r}$ $s_r$ are given. It is understood that some unknown force is also acting on the object. That is the reason the displacement is not in the same direction as that of force.

The work done by force ${\vec{f}}_{1}$ $vec f_1$ is NOT the magnitudes of ${\vec{f}}_{1}$ $vec f_1$ multiplied by ${\vec{s}}_{r}$ $vec s_r$ multiplied.

The work done by force ${\vec{f}}_{1}$ $vec f_1$ is the magnitude of ${\vec{f}}_{1}$ $vec f_1$ multiplied by the component of ${\vec{s}}_{r}$ $vec s_r$ in the direction of ${\vec{f}}_{1}$ $vec f_1$ . This is explained in the next page in detail.

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed