Vector Algebra : Multiplication of Vectors

maths > vector-algebra

Multiplication of Vectors

what you'll learn...

Overview

Multiplication of Vectors

» Two products because of orthogonality of components of vectors
→ dot product is defined for components in parallel $\vec{p} \cdot \vec{q}$ $vec p cdot vec q$ $= \vec{p} \cdot \vec{a}$ $=vec p cdot vec a$
→ cross product is defined for components in perpendicular $\vec{p} \times \vec{q}$ $vec p xx vec q$ $= \vec{p} \times \vec{b}$ $=vec p xx vec b$

two forms of multiplication

The fundamental operations of mathematics are Addition, Subtraction, Multiplication and Division.

Addition is combining two quantities and measuring the combined quantity.

Subtraction is the inverse of addition.

There are two forms of multiplications. We'll explain this.

Division is the inverse of multiplication.

A person takes $2$ $2$ apples and places them in his basket. He repeats that $3$ $3$ times in total. Effectively, the person has $2 + 2 + 2 = 2 \times 3$ $2+2+2 = 2xx3$ apples. In this, scalar quantity $2$ $2$ is repeatedly added $3$ $3$ times to get result $6$ $6$ .

A scalar quantity can be added repeatedly.
Repeated addition is a form of multiplication.

A person takes $3$ $3$ oranges that costs $10$ $10$ coins each. The person has to pay $3 \times 10 = 30$ $3xx10=30$ coins for the fruits. The scalar quantity $3$ $3$ multiplies with another scalar quantity $10$ $10$ .

Two different scalar quantities can be multiplied.

Note: In this example, the number of oranges is forming a count equivalent to multiply the cost. Instead consider, force equals mass multiplied acceleration. In this, the mass and acceleration are multiplied. Neither of them is mapped to count equivalent.

We have studied about vector addition and multiplication of vectors by a scalar.

Is there something as multiplication of a vector by another vector?
That is the subject of learning in these pages. Let us go through some basics to understand vector multiplication.

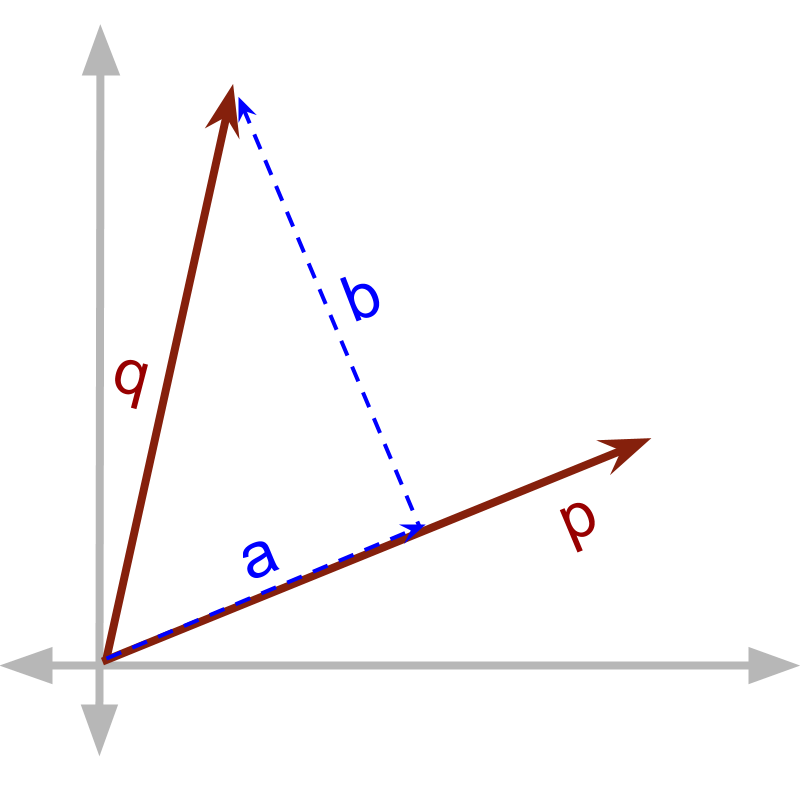
Consider the $\vec{p}$ $vec p$ and $\vec{q}$ $vec q$ shown in figure. $\vec{q}$ $vec q$ is split into $\vec{a}$ $vec a$ and $\vec{b}$ $vec b$ , such that
   $\vec{q} = \vec{a} + \vec{b}$ $vec q = vec a + vec b$ and
   $\vec{a}$ $vec a$ is in parallel to $\vec{p}$ $vec p$
   $\vec{b}$ $vec b$ is in perpendicular to $\vec{p}$ $vec p$

The vectors $\vec{p}$ $vec p$ and $\vec{q}$ $vec q$ interact to form a product. In this multiplication, either one of $\vec{a}$ $vec a$ and $\vec{b}$ $vec b$ takes part. Remember the orthogonality of directions. When vectors interact to form products the interaction is either with the component in parallel or the component in perpendicular.

When two vector quantities interact to form a product, either one of the (1) component in parallel or (2) component in perpendicular is involved in the multiplication. In practical scenarios, when one component interacts, the other component does not interact and is lost in the product.

summary

How does direction affect vector quantities in multiplication?

At an abstract level, there are two products possible. Given multiplicand $\vec{p}$ $vec p$ and multiplier $\vec{q}$ $vec q$ . $\vec{q}$ $vec q$ is split into $\vec{a}$ $vec a$ and $\vec{b}$ $vec b$ , such that
   $\vec{q} = \vec{a} + \vec{b}$ $vec q = vec a + vec b$ and
   $\vec{a}$ $vec a$ is in parallel to $\vec{p}$ $vec p$
   $\vec{b}$ $vec b$ is in perpendicular to $\vec{p}$ $vec p$

two forms of multiplications are defined for each of these two components.

• one with component in parallel to the other, called vector dot product. $\vec{p} \cdot \vec{q} = \vec{p} \cdot \vec{a}$ $vec p cdot vec q = vec p cdot vec a$

• another with component in perpendicular to the vector, called vector cross product. $\vec{p} \times \vec{q} = \vec{p} \times \vec{b}$ $vec p times vec q = vec p times vec b$

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed