Vector Algebra : Component form of Vectors

maths > vector-algebra

Component form of Vectors

what you'll learn...

Overview

Vector Component form : Revisited

» Vector Component Form is linear combination of vectors
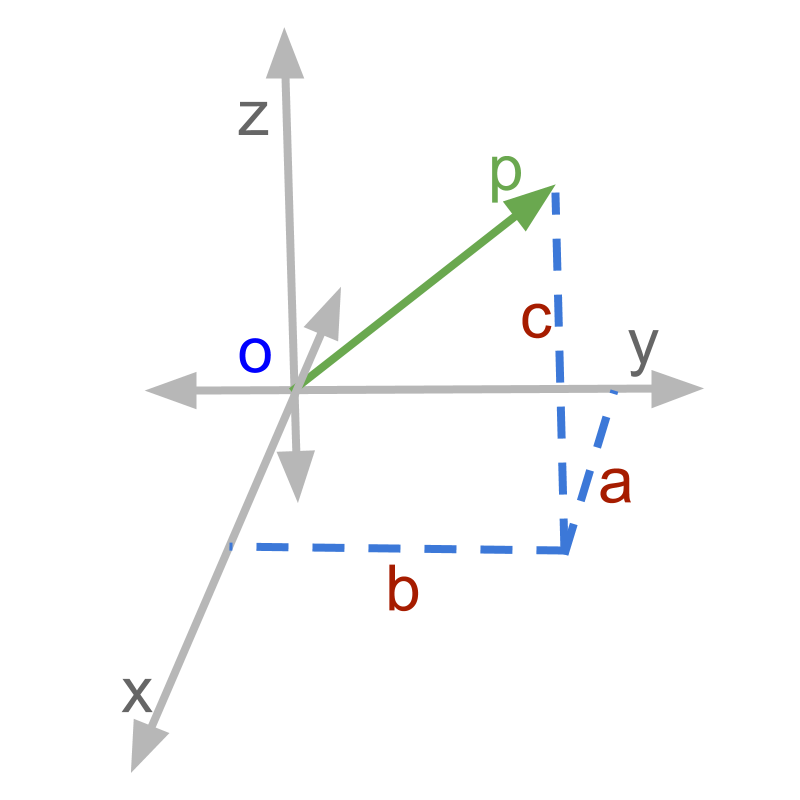    → $i$ $i$ , $j$ $j$ , $k$ $k$ are unit vectors
    → $a$ $a$ , $b$ $b$ , $c$ $c$ are scalars
    → $\vec{p} = a i + b j + c k$ $vec p = a i + b j + c k$
component form is scalar multiplication and addition of unit vectors.

components

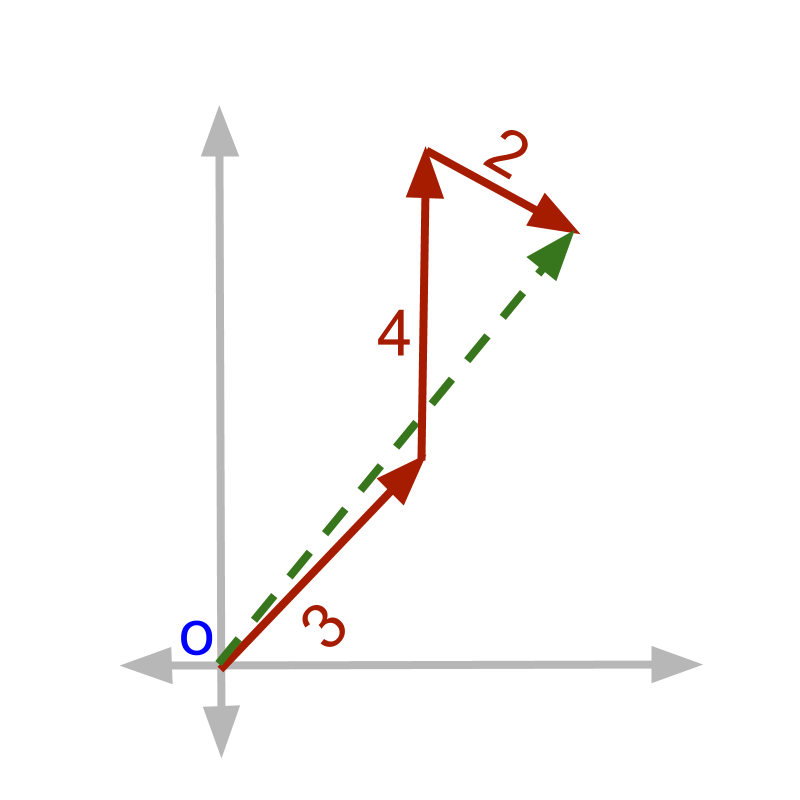
If a person walks $3$ $3$ meter north east, $4$ $4$ meter north. Then, facing north, the person turns clockwise $120^{\circ}$ $120^@$ and walk $2$ $2$ meter forward. The figure shows the problem using line segments and trigonometry is used to solve for the distance between starting position and the end position.

The solution with trigonometry is illustrated in the figure. Represent each of the segment in their horizontal and vertical components.

• $3$ $3$ north east = $3 \cos 45$ $3cos45$ east + $3 \sin 45$ $3sin45$ north

• $4$ $4$ north = $4 \cos 90$ $4cos90$ east + $4 \sin 90$ $4sin90$ north

• $2$ $2$ at $- 30^{\circ}$ $-30^@$ = $2 \cos (- 30)$ $2cos(−30)$ east + $2 \sin (- 30)$ $2sin(−30)$ north

• Add each of these east and north components individually

• $3 \cos 45 + 4 \cos 90 + 2 \cos (- 30)$ $3cos45+4cos90+2cos(−30)$ $= 3.85$ $= 3.85$

• $3 \sin 45 + 4 \sin 90 + 2 \sin (- 30)$ $3sin45+4sin90+2sin(−30)$ $= 5.12$ $= 5.12$

• result distance $= 3.85$ $= 3.85$ east $+ 5.12$ $+5.12$ north

The solution is made simple when the vector quantities are split into components having same direction, as (east and north), With which the addition was easy.

This observation lead to specifying the quantities differently in the first place.

• $3$ $3$ north east = $3 \cos 45$ $3cos45$ east + $3 \sin 45$ $3sin45$ north
• $4$ $4$ north = $4 \cos 90$ $4cos90$ east + $4 \sin 90$ $4sin90$ north
• $2$ $2$ at $- 30^{\circ}$ $-30^@$ = $2 \cos (- 30)$ $2cos(−30)$ east + $2 \sin (- 30)$ $2sin(−30)$ north
The left hand side specifies the magnitude and direction. Where as the right hand side specifies component along the two axes, namely, east and north.

In vector form, we choose to represent in the format given in right hand side. A 3D vector is given as a sum of components along three dimensions, which is equivalently a sum of scalar multiples of the three unit vectors.

This is a delightful learning.

• We studied about the vector representation as $a i + b j + c k$ $ai+bj+ck$ .

• Then, we studied about orthogonality of directions and 3D space is represented with 3 dimensions.

• Then, we studied about scalar multiple of vectors.

• Then, we studied about representing a vector as linear combination of several vectors. $\vec{x} = a \vec{p} + b \vec{q}$ $vec x = a vec p + b vec q$ where $a, b \in ℝ$ $a,b in RR$

• Then, connecting all these, the vector representation $a i + b j + c k$ $ai+bj+ck$ is explained as

→ $i$ $i$ , $j$ $j$ , $k$ $k$ are the standard unit vectors along $x -, y -, z -$ $x-, y-, z-$ axes representing the 3D space.

→ Any vector in 3D space is represented as linear combination of the unit vectors $i$ $i$ , $j$ $j$ , $k$ $k$ as $a i + b j + c k$ $ai+bj+ck$ .

summary

Vector Component form: Component form of vector representation is the sum of standard unit vector $i$ $i$ , $j$ $j$ , $k$ $k$ multiplied by scalars $a, b, c \in ℝ$ $a, b, c in RR$ .
$\vec{p} = a i + b j + c k$ $vec p = a i + bj + ck$

Vector representation is chosen to be sum of standard unit vectors multiplied by scalars.

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed