Vector Algebra : Directional Cosine

maths > vector-algebra

Directional Cosine

what you'll learn...

Overview

Directional Cosine

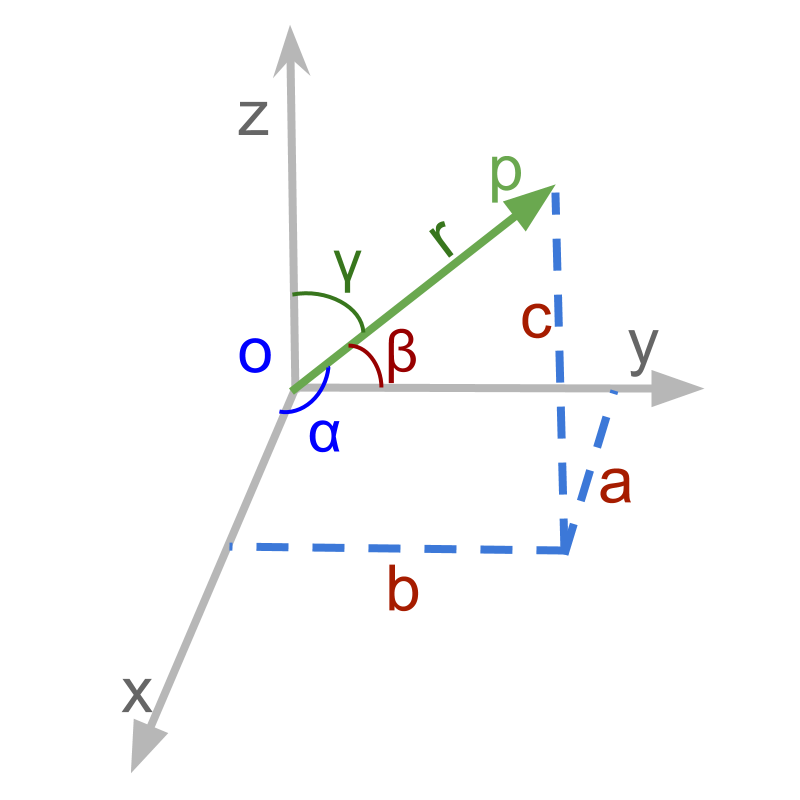» Directional cosines:

    → $\vec{p} = a i + b j + c k$ $vec p = ai+bj+ck$ makes angles $α, β, γ$ $alpha,beta,gamma$ with $x, y, z$ $x,y,z$ -axes respectively

    → $\cos α = \frac{a}{| p |}$ $cos alpha= a/(|p|)$

    → $\cos β = \frac{b}{| p |}$ $cos beta= b/(|p|)$

    → $\cos γ = \frac{c}{| p |}$ $cos gamma= c/(|p|)$

alternate representation

'cosine ' of an angle is 'the ratio of adjacent side (adjacent to the given angle) to the hypotenuse in a right angled triangle'.

While referring to vector quantities, we use the form that specifies the components along the axes. eg: $a i + b j + c k$ $ai+bj+ck$ specifies the component along $x -$ $x-$ axis is $a$ $a$ , the component along $y -$ $y-$ axis is $b$ $b$ , and the component along $z -$ $z-$ axis is $c$ $c$ .

The alternate representation to component form is to specify magnitude and angles made by the vector on the axes. This has the necessary information about the vector.

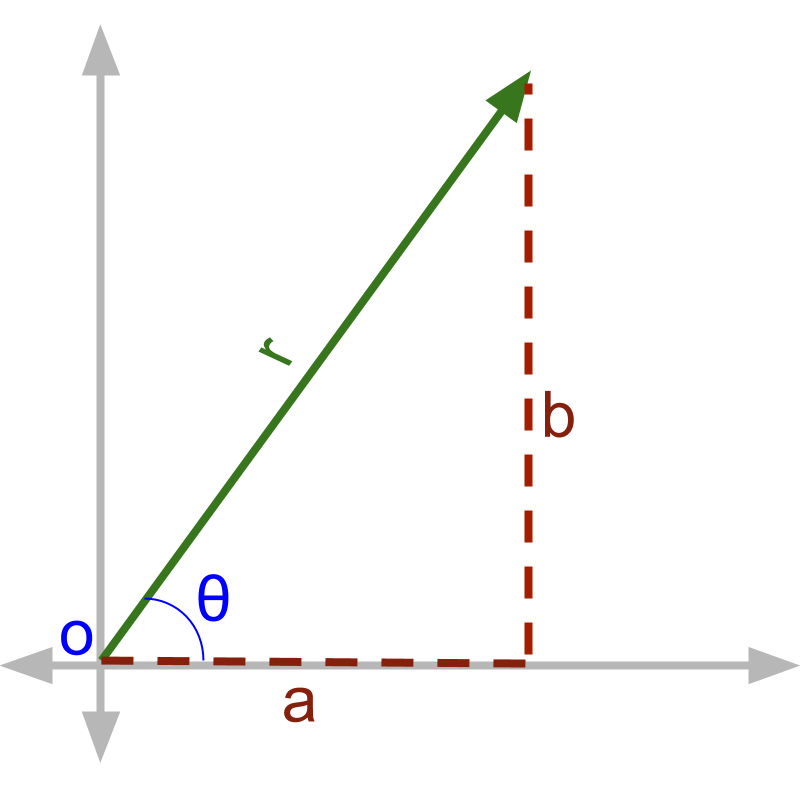
To describe the vector $a i + b j$ $ai+bj$ shown in the figure, if ' $r$ $r$ and $θ$ $theta$ ' are available we can derive the vector form $a i + b j$ $ai+bj$ .

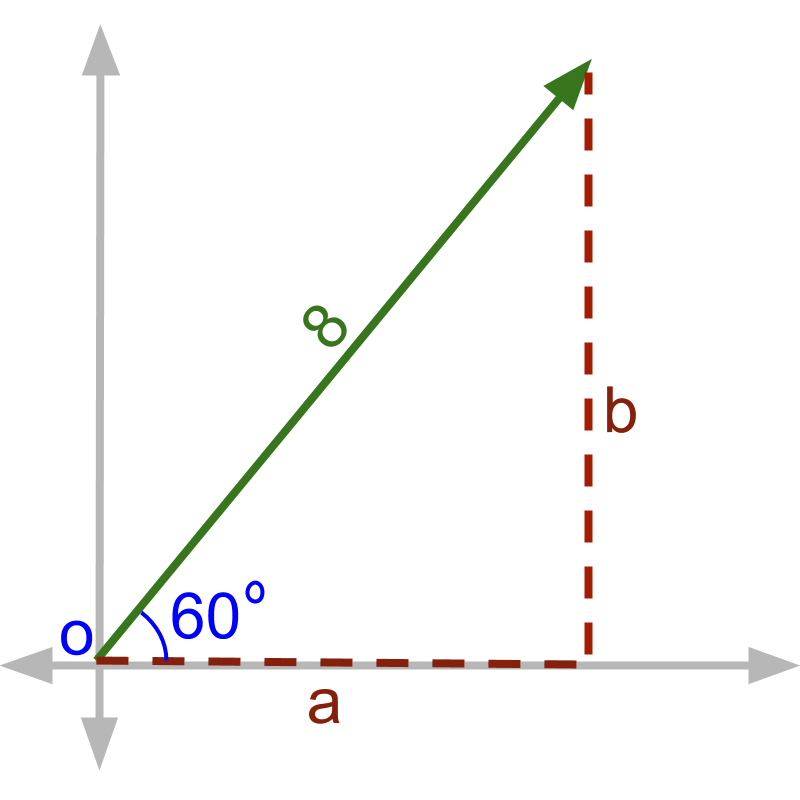
example of directional cosine of 2D vector

It is noted that the values of $a$ $a$ and $b$ $b$ in the figure are ' $a = 8 \cos 60$ $a=8 cos 60$ and $b = 8 \sin 60$ $b=8 sin 60$ '.

The same in 3D, to describe the vector $a i + b j + c k$ $ai+bj+ck$ shown in figure, the vector is completely defined by ' $r$ $r$ and $α, β$ $alpha, beta$ '. If these three parameters are available we can derive the vector notation $a i + b j + c k$ $ai+bj+ck$ .

Note that the third angle can be derived from the other two angles.

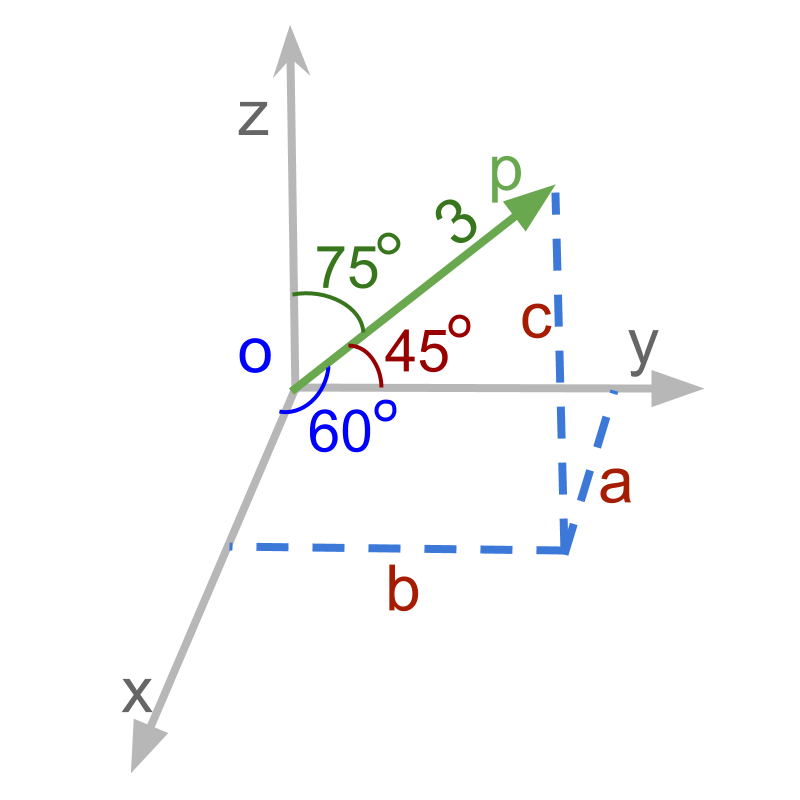
example of directional cosine of 3D vector

Given the vector in figure, values of $a$ $a$ , $b$ $b$ , and $c$ $c$ are derived as $a = 3 \cos 60$ $a=3cos60$ ; $b = 3 \cos 45$ $b=3cos45$ ; $c = 3 \cos 75$ $c=3cos75$

When a vector with magnitude $r$ $r$ and angles $α, β, γ$ $alpha,beta,gamma$ is given, the coordinate form of the vector is
$r (\cos α i + \cos β j + \cos γ k)$ $r(cos alpha i+cos beta j+cos gamma k)$
$\cos α$ $cos alpha$ , $\cos β$ $cos beta$ , $\cos γ$ $cos gamma$ are called the directional cosines of the vector.

The representation of vectors in the component form is $\vec{p} = a i + b j + c k$ $vec p = ai+bj+ck$
Directional cosines along with magnitude provide an alternate representation of a vector.
$\vec{p} = r (\cos α i + \cos β j + \cos γ k)$ $vec p = r (cos alpha i + cos beta j + cos gamma k)$

$\cos α = \frac{a}{r}$ $cos alpha =a/r$

$\cos β = \frac{b}{r}$ $cos beta =b/r$

$\cos γ = \frac{c}{r}$ $cos gamma =c/r$

$r^{2} = a^{2} + b^{2} + c^{2}$ $r^2=a^2+b^2+c^2$

$\cos^{2} α + \cos^{2} β + \cos^{2} γ = 1$ $cos^2 alpha + cos^2 beta + cos^2 gamma = 1$

Directional cosines make Unit Vector: For a given vector $a i + b j + c k$ $ai+bj+ck$ the directional cosine vector $l i + m j + n k$ $li+mj+nk$ is the unit vector in the direction of the given vector. Note that

$l = \cos α = \frac{a}{r}$ $l = cos alpha =a/r$

$m = \cos β = \frac{b}{r}$ $m = cos beta =b/r$

$n = \cos γ = \frac{c}{r}$ $n = cos gamma =c/r$
This also implies that

$l^{2} + m^{2} + n^{2} = 1$ $l^2+m^2+n^2=1$

examples

What is the magnitude of the directional cosines vector : $\cos α i + \cos β j + \cos γ k$ $cos alpha i+cos beta j+cos gamma k$ ?

The answer is ' $1$ $1$ '. The magnitude = $\sqrt{\cos^{2} α + \cos^{2} β + \cos^{2} γ}$ $sqrt(cos^2 alpha+cos^2 beta+cos^2 gamma)$ , which evaluates to 1.

Find the direction cosines of a line which makes equal angles with the coordinate axes.

The answer is
$(\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}})$ $(1/sqrt(3),1/sqrt(3),1/sqrt(3))$ OR $(- \frac{1}{\sqrt{3}}, - \frac{1}{\sqrt{3}}, - \frac{1}{\sqrt{3}})$ $(-1/sqrt(3),-1/sqrt(3),-1/sqrt(3))$

From the question, we know that $α = β = γ$ $alpha=beta=gamma$ and We know the property of directional cosines $\cos^{2} α + \cos^{2} β + \cos^{2} γ = 1$ $cos^2 alpha+cos^2 beta+cos^2 gamma = 1$

If a line makes angles $45, 135, 90$ $45,135, 90$ with the x, y and z-axes respectively, find its direction cosines.

The answer is ' $\cos 45, \cos 135, \cos 90$ $cos45, cos135, cos90$ '.

Find the directional cosine of the vector $2 i - 3 j + \sqrt{3} k$ $2i-3j+sqrt(3)k$ .

magnitude of the vector = 4
So directional cosines are $\frac{2}{4}, - \frac{3}{4}, \frac{\sqrt{3}}{4}$ $2/4 , -3/4, sqrt(3)/4$

summary

Directional cosines: Given that a vector $\vec{p} = a i + b j + c k$ $vec p = ai+bj+ck$ makes angles $α, β, γ$ $alpha,beta,gamma$ with $x, y, z$ $x,y,z$ -axes respectively, then the directional cosines of the vector are
$\cos α = \frac{a}{| p |}$ $cos alpha= a/(|p|)$
$\cos β = \frac{b}{| p |}$ $cos beta= b/(|p|)$
$\cos γ = \frac{c}{| p |}$ $cos gamma= c/(|p|)$

Directional cosines are the ratio of "projections on to an axes" to "the magnitude".

Directional cosines make Unit Vector: For a given vector $a i + b j + c k$ $ai+bj+ck$ the directional cosine vector $l i + m j + n k$ $li+mj+nk$ is the unit vector in the direction of the given vector. Note that

$l = \cos α = \frac{a}{r}$ $l = cos alpha =a/r$

$m = \cos β = \frac{b}{r}$ $m = cos beta =b/r$

$n = \cos γ = \frac{c}{r}$ $n = cos gamma =c/r$
This also implies that

$l^{2} + m^{2} + n^{2} = 1$ $l^2+m^2+n^2=1$

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed