Vector Algebra : Cross Product: First Principles

maths > vector-algebra

Cross Product: First Principles

what you'll learn...

Overview

Vector Cross Product : First Principles

» multiplied with component in perpendicular
    → $\vec{p} \times \vec{q}$ $vec p xx vec q$ $= \vec{p} \times \vec{b}$ $=vec p xx vec b$ $= | \vec{p} | | \vec{b} | \hat{n}$ $= |vec p||vec b| hat n$

    → product of magnitudes of components in perpendicular

    → direction perpendicular to both the vectors

in perpendicular

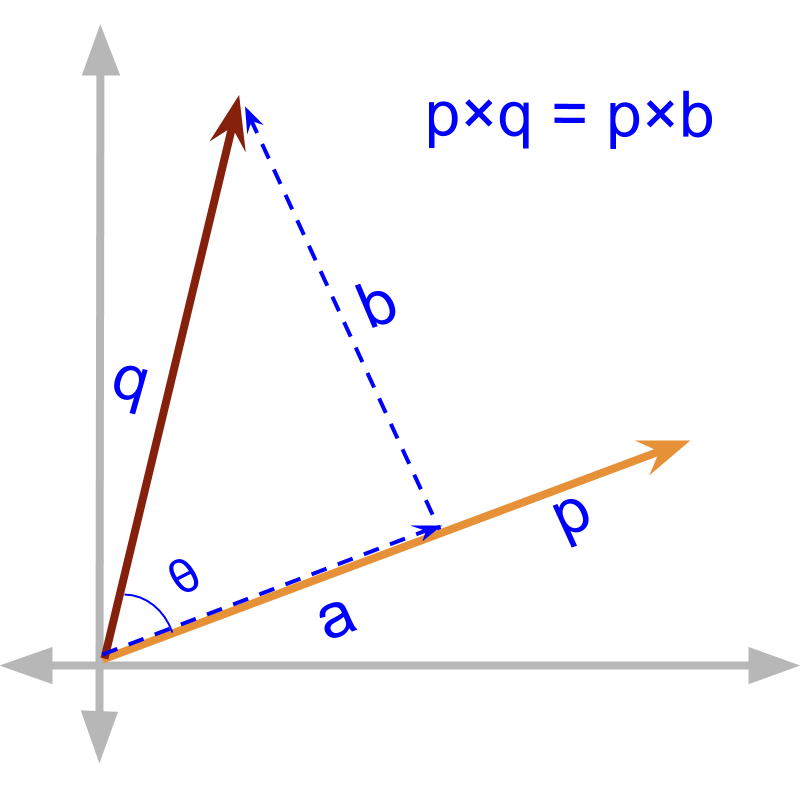
The product where vector components in perpendicular interact is defined. Given vectors $\vec{p}$ $vec p$ and $\vec{q}$ $vec q$ as shown in figure. The component of $\vec{q}$ $vec q$ perpendicular to the $\vec{p}$ $vec p$ us $\vec{b}$ $vec b$

The angle between the vectors is $θ$ $theta$ . Then $| \vec{b} |$ $|vec b|$ $= | q | \sin θ$ $= |q|sin theta$

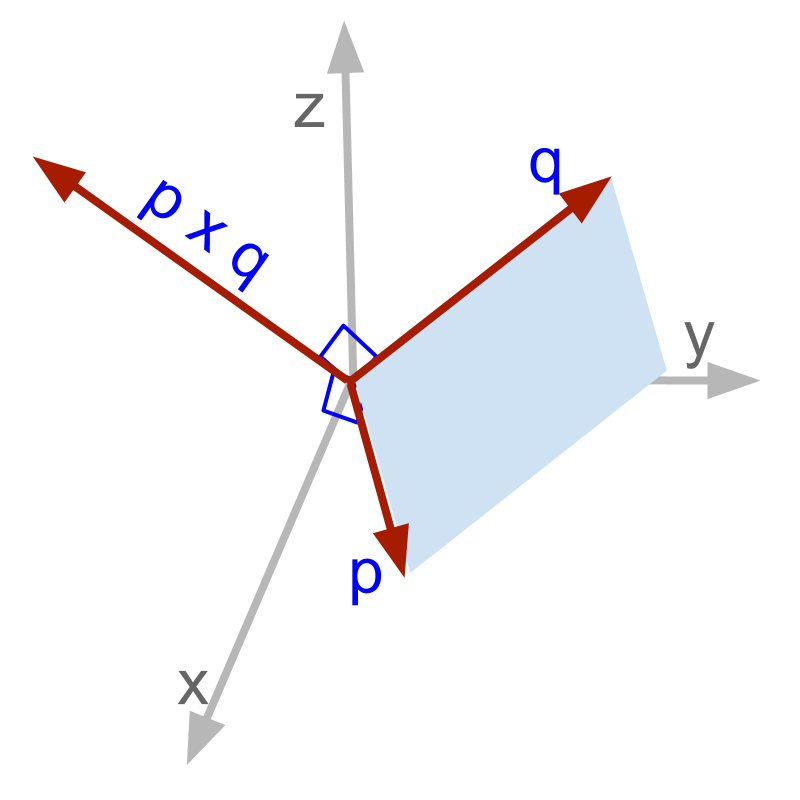
What will be a good choice of direction of the product between components in perpendicular?

Two intersecting lines, which are not parallel, define a plane. The normal on the face of the plane describes the plane and so, the normal is taken as the direction of the product.

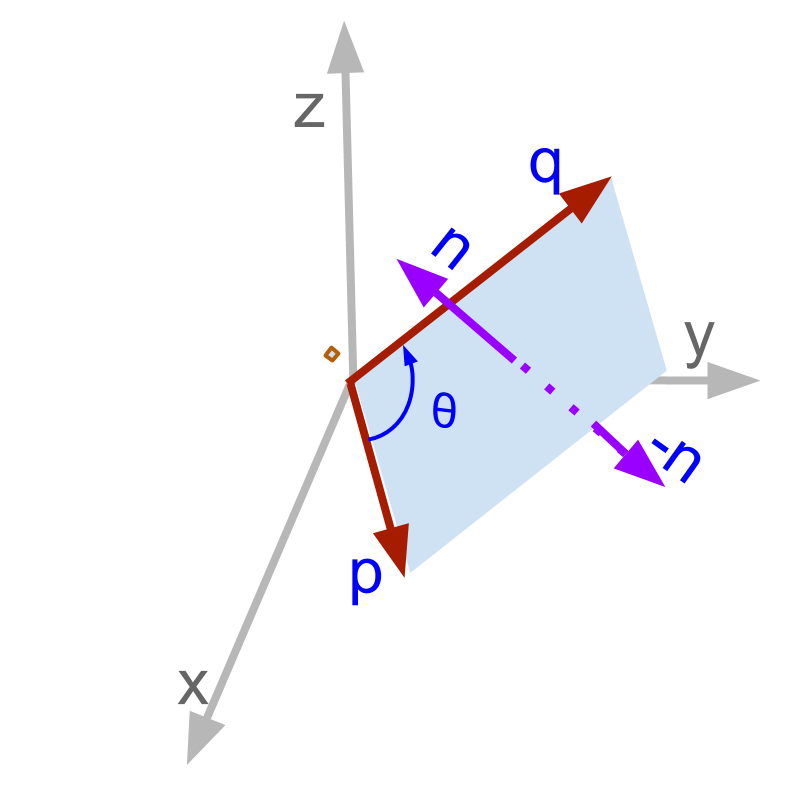
vector cross product choice of directions

A plane can be described by

• normal which is one side of the plane, or

• the negative of the normal, which is the other side of the plane.

One of this can be chosen as the direction of cross product $\vec{p} \times \vec{q}$ $vec p xx vec q$ .

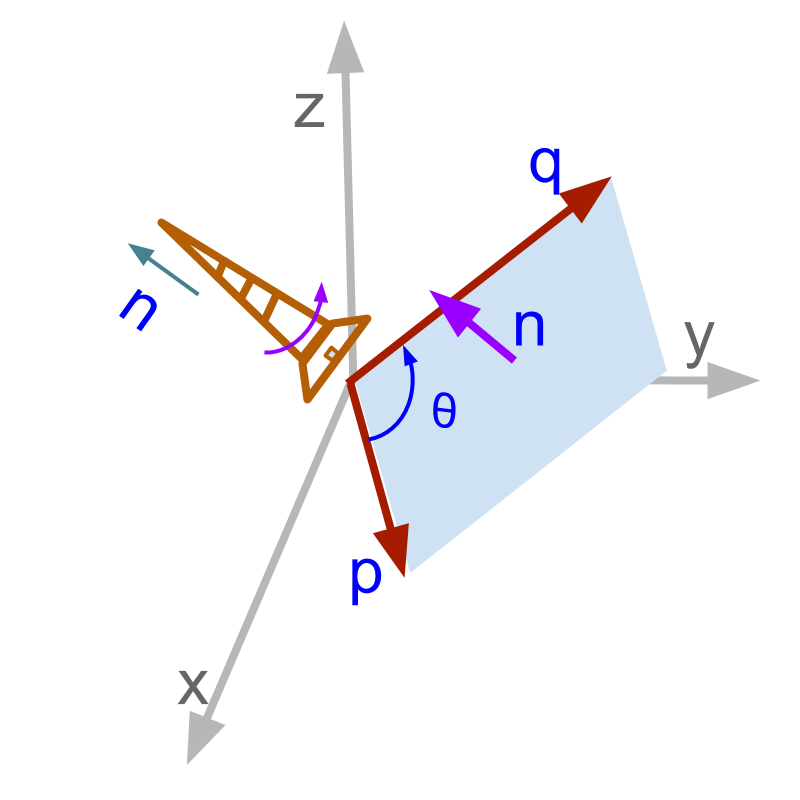
vector cross product standard screw direction

The direction of the cross product $\vec{p} \times \vec{q}$ $vec p xx vec q$ is shown in the figure. In a standard right-handed rectangular coordinate system,
The direction in which a standard screw advances when it turns from $\vec{p}$ $vec p$ to $\vec{q}$ $vec q$ , defines the normal. s

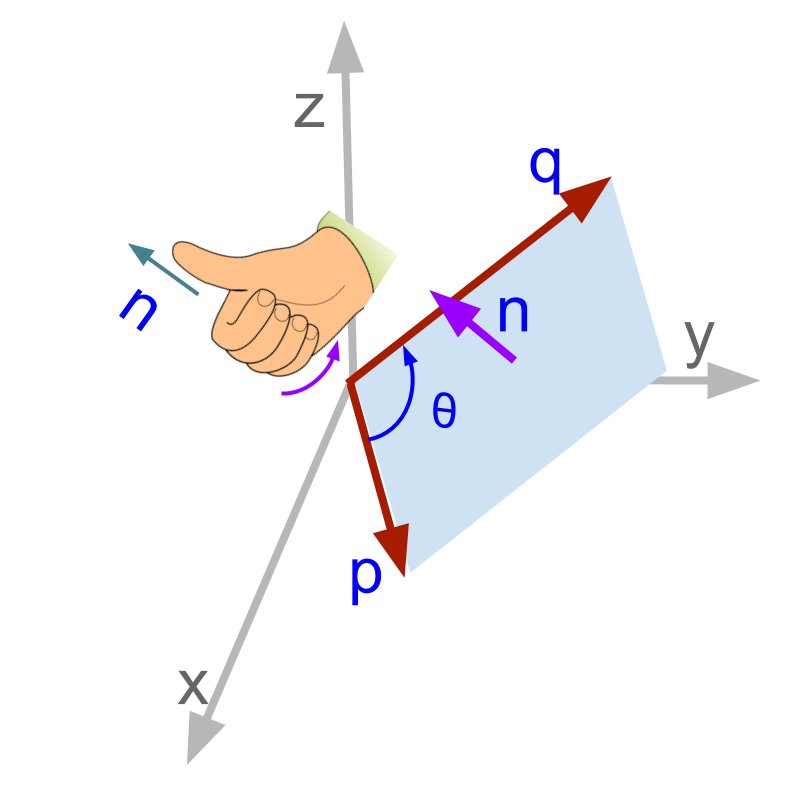
vector cross product right hand thumb rule for direction

Another form to find the direction of the cross product $\vec{p} \times \vec{q}$ $vec p xx vec q$ is shown in the figure. In a standard right-handed rectangular coordinate system,
The direction pointed by the right thumb when fingers are curled to point from $\vec{p}$ $vec p$ to $\vec{q}$ $vec q$ , defines the normal.

Formal definition of vector cross product.
$\vec{p} \times \vec{q} = | p | | q | \sin θ \hat{n}$ $vec p xx vec q = |p||q|sin theta hat n$ where $\hat{n}$ $hat n$ is the normal denoting the direction of right handed rotation from $\vec{p}$ $vec p$ to $\vec{q}$ $vec q$ .

summary

Vector Cross Product: for vectors $\vec{p}, \vec{q} \in R^{3}$ $vec p, vec q in bbb(R)^3$
$\vec{p} \times \vec{q} = (| p | | q | \sin θ) \hat{n}$ $vec p xx vec q = (|p||q|sin theta ) hat n$
where $\hat{n}$ $hat n$ is the unit vector of right-handed rotation from $\vec{p}$ $vec p$ to $\vec{q}$ $vec q$ .

Vector Cross Product is defined as the product of components in perpendicular.

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed