Vector Algebra : Vector and Coordinate Geometry

maths > vector-algebra

Vector and Coordinate Geometry

what you'll learn...

Overview

Vector and Coordinate Geometry

» Vector Algebra in Coordinate Geometry

    → Vector representation can be used to describe points in coordinate space.

    → $p (x, y, z) \leftrightarrow x i + y j + z k$ $p(x,y,z) harr x i + y j + z k$

    → Distance between origin and the point is the magnitude of the vector.

Vector Algebra can be used to solve probems in coordinate geometry.

» Coordinate Geometry in Vector Algebra

    → Vectors are directed line segments in coordinate space

    → Magnitude is the distance between initial and terminal points

    → Relative properties of vectors, like, angle between vectors, are preserved

Properties and results of coordinate geometry can be used to solve vector algebra problems

two forms

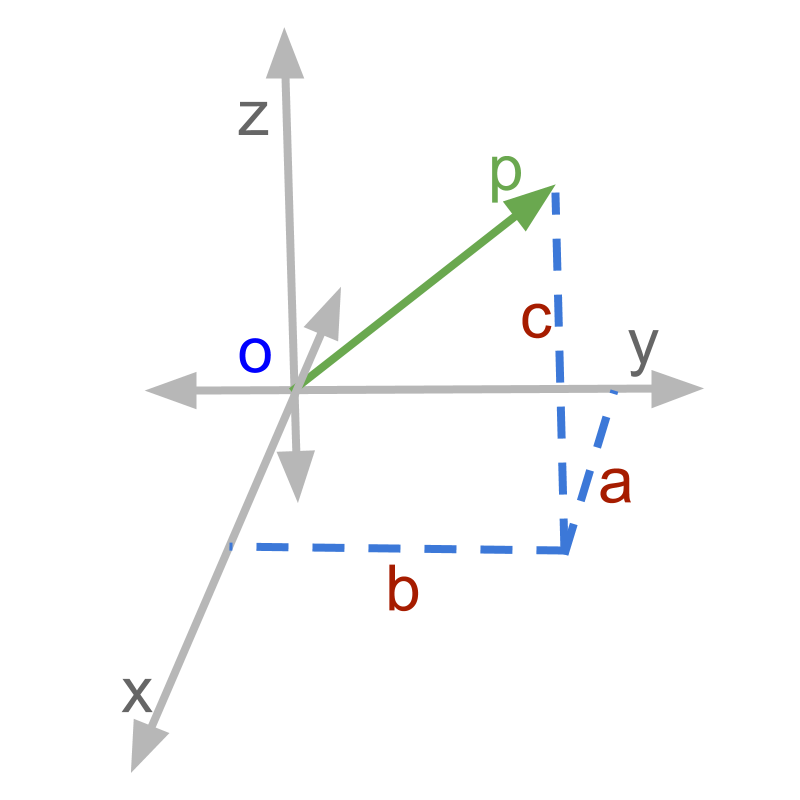
Vectors are quantities with magnitude and direction.

In the mathematical representation of vectors, the components along 3D coordinates are described individually. The representation of a vector is given as $\vec{p} = a i + b j + c k$ $vec p = ai+bj+ck$

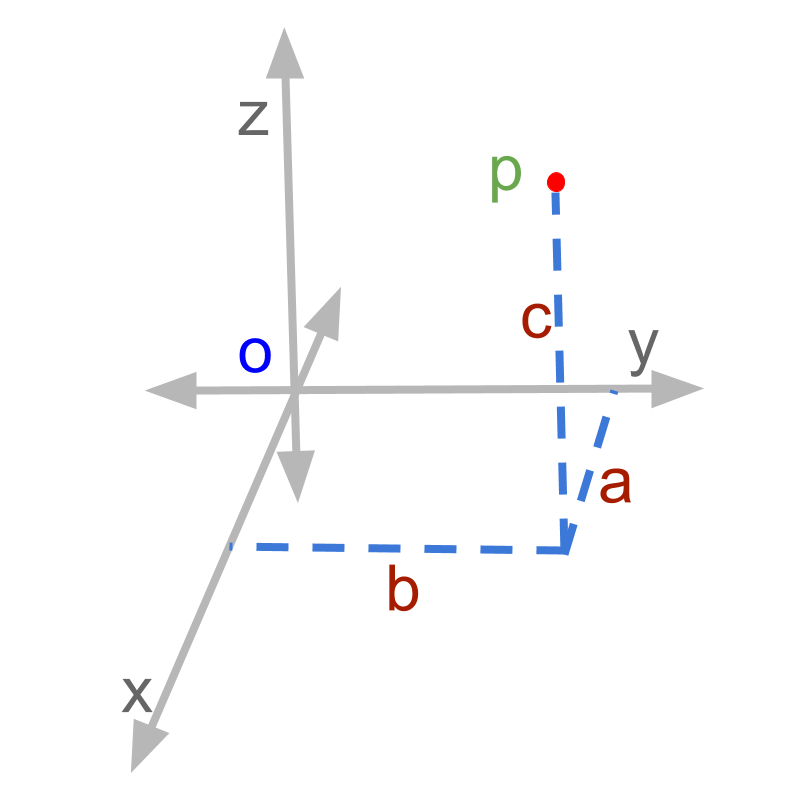
vector algebra for coordinate geometry example

Coordinate Geometry is the system of geometry where the position of points on the 3D coordinates are described as ordered pairs of numbers corresponding to the three axes. This aims at studying relations and properties of shapes including points, lines, surfaces, and solids. The representation of point ' $p$ $p$ ' is given as (a,b,c)`

Vector Algebra definition of a vector starting from origin and ending at point $p$ $p$ is

• $a i + b j + c k$ $ai+bj+ck$

and Coordinate geometry definition of a point $p$ $p$ is

• $(a, b, c)$ $(a,b,c)$

These two similar look very similar.

In the coming pages, We will see

• How Vector algebra can be used in coordinate geometry problems, and

• How coordinate geometry principles or results are used to solve vector algebra problems.

distance between points

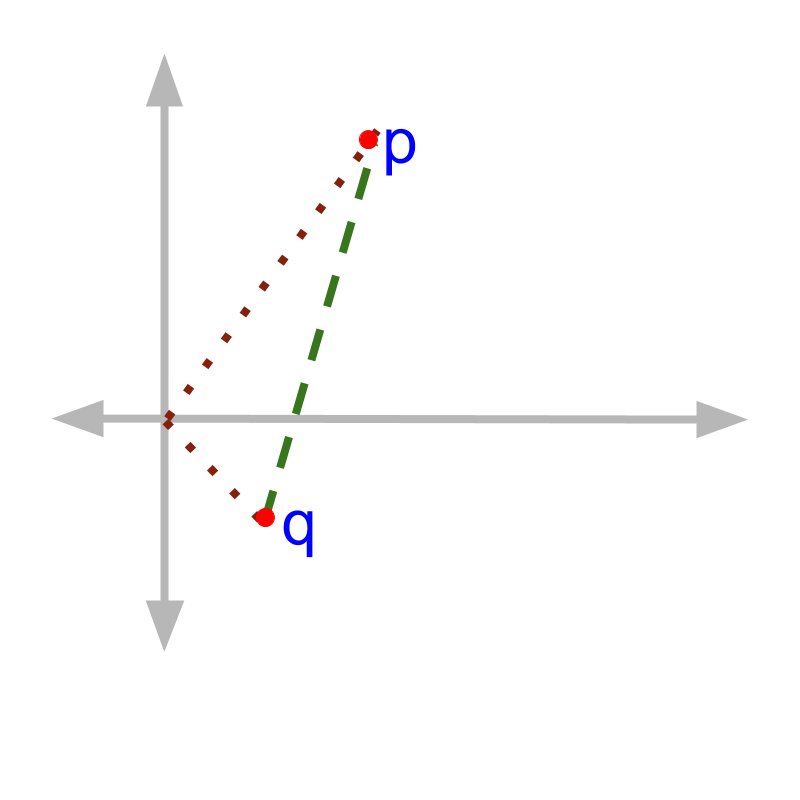
vector algebra for coordinate geometry problems

The distance between point $p (2, 3)$ $p(2,3)$ and point $q (1, - 1)$ $q(1,-1)$ is $\sqrt{{(2 - 1)}^{2} + {(3 - (- 1))}^{2}}$ $sqrt((2-1)^2+(3-(-1))^2)$

In general terms Distance between points $p (x_{1}, y_{1})$ $p(x_1, y_1)$ and point $q (x_{2}, y_{2})$ $q(x_2,y_2)$ is given by $\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ $sqrt((x_1-x_2)^2+(y_1-y_2)^2)$

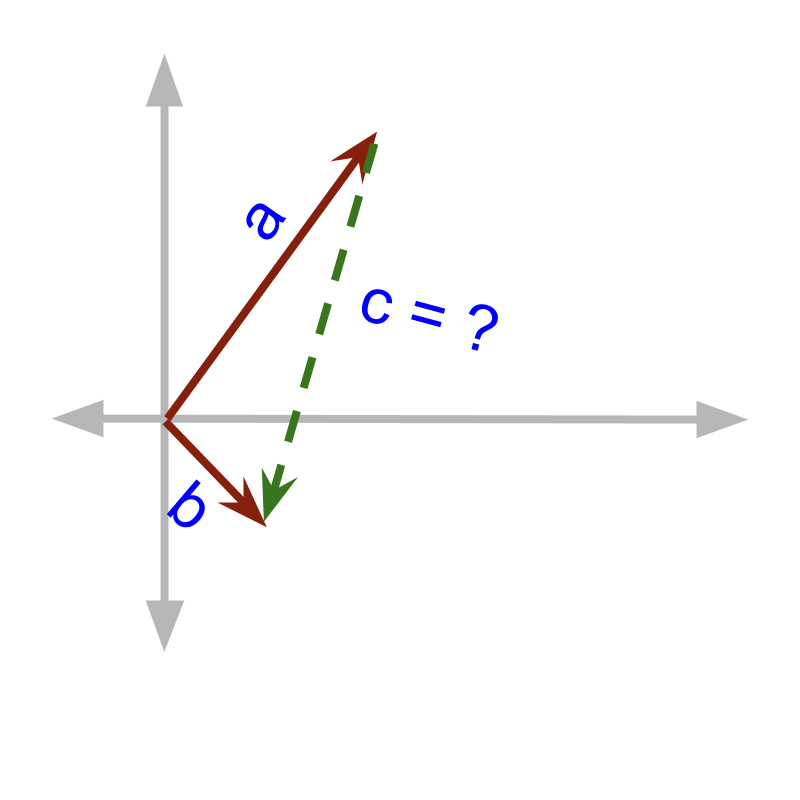
Consider the points $p (2, 3)$ $p(2,3)$ and point $q (1, - 1)$ $q(1,-1)$ as vectors $\vec{a} = 2 i + 3 j$ $vec a=2i+3j$ and $\vec{b} = i - j$ $vec b=i-j$ . The distance between two vectors

$| \vec{b} - \vec{a} |$ $|vec b - vec a|$

$= | (1 - 2) i + (- 1 - 3) j |$ $=|(1-2)i+(-1-3)j|$

$\sqrt{{(1 - 2)}^{2} + {(- 1 - 3)}^{2}}$ $sqrt((1-2)^2+(-1-3)^2)$

You are not yet introduced to vector addition and subtraction. But it is intuitive to see from the figure that the $\vec{c}$ $vec c$ can be traced as negative of $\vec{a}$ $vec a$ and then $\vec{b}$ $vec b$ .

With the two problems, it is illustrated that the vector algebra can be used to solve coordinate geometry problems.

equivalence

A point in coordinate plane is equivalently a vector with origin as initial point, and the given point as terminal point.

The word 'initial' means 'starting; beginning'.

The word 'terminal ' means 'end; concluding'.

example

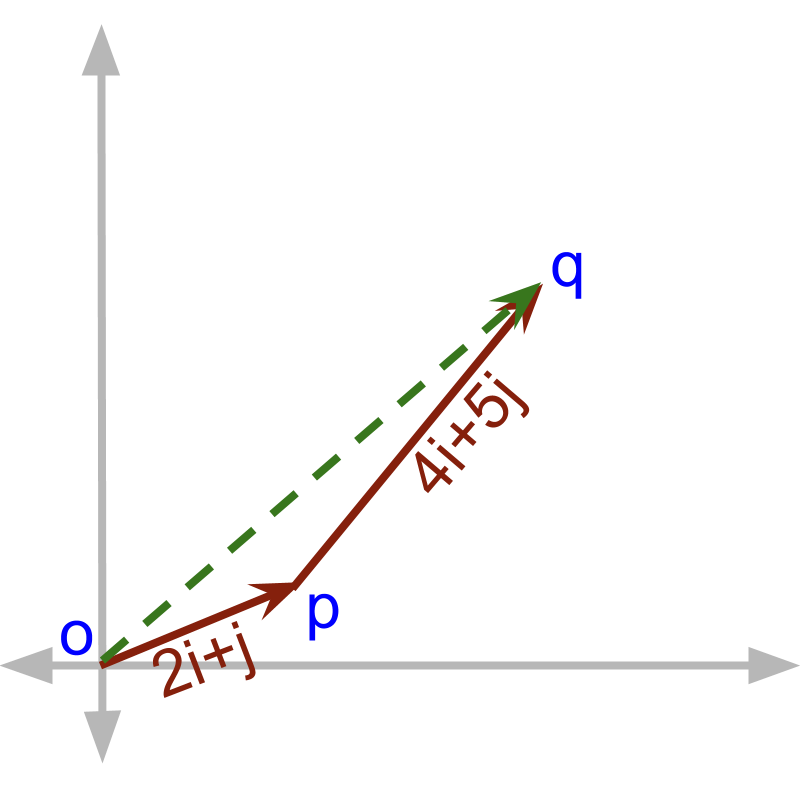
A person walks $2 i + j$ $color(deepskyblue)(2i+j)$ ( $2$ $2$ meter towards east and $1$ $1$ meter towards north) . Then the person walks $4 i + 5 j$ $color(coral)(4i+5j)$ . What is the distance between the starting and end positions?

The answer is ' $2 i + j + 4 i + 5 j$ $color(deepskyblue)(2i+j)+color(coral)(4i+5j)$ ', which is quite intuitive from the given figure.

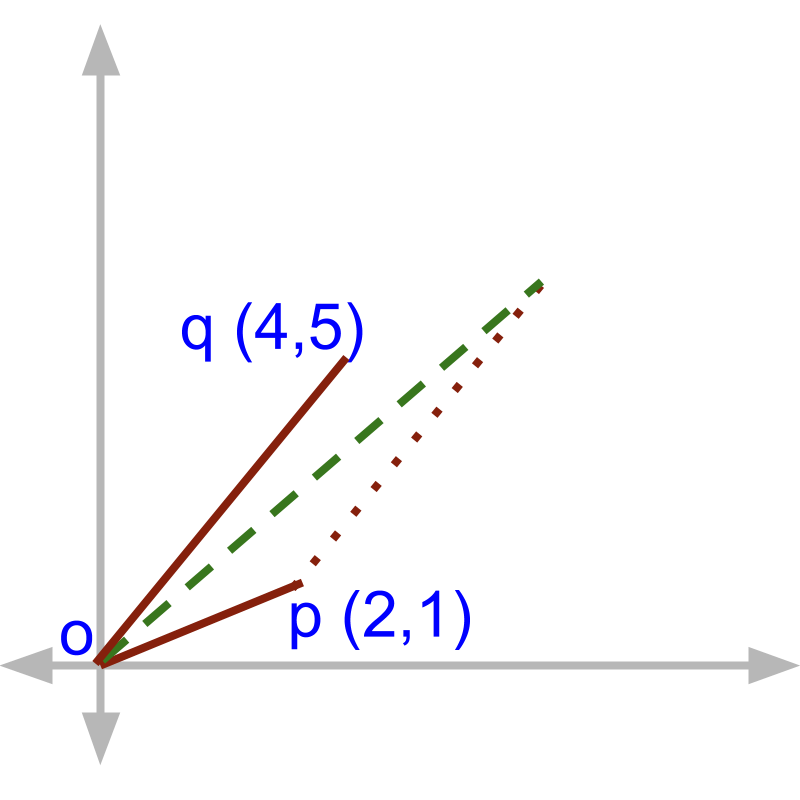
coordinate geometry for vector algebra example 2

Given the points $p (2, 1)$ $color(deepskyblue)(p(2,1))$ and $q (4, 5)$ $color(coral)(q(4,5))$ . What is the end point on the 3rd side of the triangle formed by two line segments $\bar{o p}$ $bar(op)$ and a line parallel and equal in length to $\bar{o q}$ $bar(oq)$ starting at point $p$ $p$ ?

The answer is ' $(2 + 4, 1 + 5)$ $(color(deepskyblue)(2)+color(coral)(4), color(deepskyblue)(1)+color(coral)(5))$ ', which is quite evident from the given figure.

With the two problems, it is illustrated that the vectors can be considered as line segments in coordinate geometry. The results of 'geometry' can be used to solve vector algebra problems.

application note

This abstraction into linesegments is applied for vectors that in its true form are not line segments. Some of the following examples are abstracted as line segments are

• force

• acceleration

• velocity

• displacement

• electric flux density

• etc.

Even though these quantities are not 'line segments' these are abstracted as line segments and coordinate geometry principles are used.

directed line-segment

Given the points $A (3, 4, 1)$ $A (3,4,1)$ and point $B (2, 2, 4)$ $B (2,2,4)$ , a line from point $A$ $A$ to point $B$ $B$ is equivalently a vector $\vec{A B}$ $vec(AB)$

This is named as directed line segment.

The word 'directed' means 'having a specified direction'. For a directed line segment, the initial position and the terminal point are specified. In contrast, a line segment is a line between two points, without identifying one as initial and the other as terminal.

Directed Line Segment: A line from initial point $A (x_{a}, y_{a}, z_{a})$ $A (color(deepskyblue)(x_a, y_a, z_a))$ to terminal point $B (x_{b}, y_{b}, z_{b})$ $B (color(coral)(x_b, y_b, z_b))$ is a directed line segment, and equivalently a vector

• $\vec{A B} = (x_{b} - x_{a}) i + (y_{b} - y_{a}) j + (z_{b} - z_{a}) k$ $vec(AB) = (color(coral)(x_b)-color(deepskyblue)(x_a))i+(color(coral)(y_b)-color(deepskyblue)(y_a))j+(color(coral)(z_b)-color(deepskyblue)(z_a))k$

• Point $A$ $A$ is the initial point.

• Point $B$ $B$ is the terminal point.

• Length of the line segment is the magnitude of $\vec{A B}$ $vec(AB)$ .

Line segment with an initial point to a terminal point specified is a directed line segment.

A vector is a directed line segment in coordinate plane.

Abstraction of Vectors in Coordinate Geometry: Vectors can be abstracted as directed line segments.

• Magnitude of a vector is the length of the line segment.

• Relative properties of vectors, like angle between vectors, are preserved in this abstraction.

• Properties or results of coordinate geometry can be used to solve vector algebra problems.

• The abstracted vectors can be equivalently moved to any position on the coordinate plane, with magnitude and direction preserved.

examples

Find the vector between points $A (1, - 3.2, - 1)$ $A (1, -3.2, -1)$ and $B (2, 1, 2.1)$ $B (2, 1, 2.1)$

The answer is ' $\vec{A B} = i + 4.2 j + 3.1 k$ $vec(AB)= i+4.2j+3.1k$ '

What is the angle between the two forces ${\vec{f}}_{1} = 3 i$ $vec f_1 = 3i$ and ${\vec{f}}_{2} = 4 j$ $vec f_2 = 4j$ ?

The answer is ' $90^{\circ}$ $90^@$ '. The force can be abstracted as directed line segment in coordinate plane. Thus, $f_{1} = (3, 0)$ $f_1 = (3,0)$ and $f_{2} = (0, 4)$ $f_2 = (0,4)$ . These points are in $x$ $x$ and $y$ $y$ axes and so the angle is $90^{\circ}$ $90^@$ .

what is the distance between points $O (0, 0)$ $O (0,0)$ and $P (2, 3)$ $P (2,3)$ ? The answer is 'both the above'. Points in coordinate plane can be modeled as vectors and vector algebra can be used.

summary

Using Vector Algebra in Coordinate Geometry: Vector representation can be used to describe points in Coordinate geometry.

• point $p (x_{1}, y_{1}, z_{1})$ $p(x_1,y_1,z_1)$ is equivalently a vector $\vec{p} = x_{1} i + y_{1} j + z_{1} k$ $vec p = x_1 i + y_1j+z_1k$

• Distance between origin and the point is the magnitude of a vector.

Vector algebra can be used to solve problems in coordinate geometry.

Directed Line Segment: A line from initial point $A (x_{a}, y_{a}, z_{a})$ $A (color(deepskyblue)(x_a, y_a, z_a))$ to terminal point $B (x_{b}, y_{b}, z_{b})$ $B (color(coral)(x_b, y_b, z_b))$ is a directed line segment, and equivalently a vector

• $\vec{A B} = (x_{b} - x_{a}) i + (y_{b} - y_{a}) j + (z_{b} - z_{a}) k$ $vec(AB) = (color(coral)(x_b)-color(deepskyblue)(x_a))i+(color(coral)(y_b)-color(deepskyblue)(y_a))j+(color(coral)(z_b)-color(deepskyblue)(z_a))k$

• Point $A$ $A$ is the initial point.

• Point $B$ $B$ is the terminal point.

• Length of the line segment is the magnitude of $\vec{A B}$ $vec(AB)$ .

Abstraction of Vectors in Coordinate Geometry: Vectors can be abstracted as directed line segments.

• Magnitude of a vector is the length of the line segment.

• Relative properties of vectors, like angle between vectors, are preserved in this abstraction.

• Properties or results of coordinate geometry can be used to solve vector algebra problems.

• The abstracted vectors can be equivalently moved to any position on the coordinate plane, with magnitude and direction preserved.

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed