Vector Algebra : Vector Dot Product : First Principles

maths > vector-algebra

Vector Dot Product : First Principles

what you'll learn...

Overview

Vector Dot Product: First Principles

» multiplied with component in parallel
→ $\vec{p} \cdot \vec{q}$ $vec p cdot vec q$ $= \vec{p} \cdot \vec{a}$ $=vec p cdot vec a$ $= | \vec{p} | | \vec{a} |$ $= |vec p||vec a|$
→ product of magnitudes of components in parallel

in parallel

We have developed the understanding that
• In some application scenarios, effect will be in the same direction as that of the cause.
• the observed effect can be sum of the effects of multiple different causes.

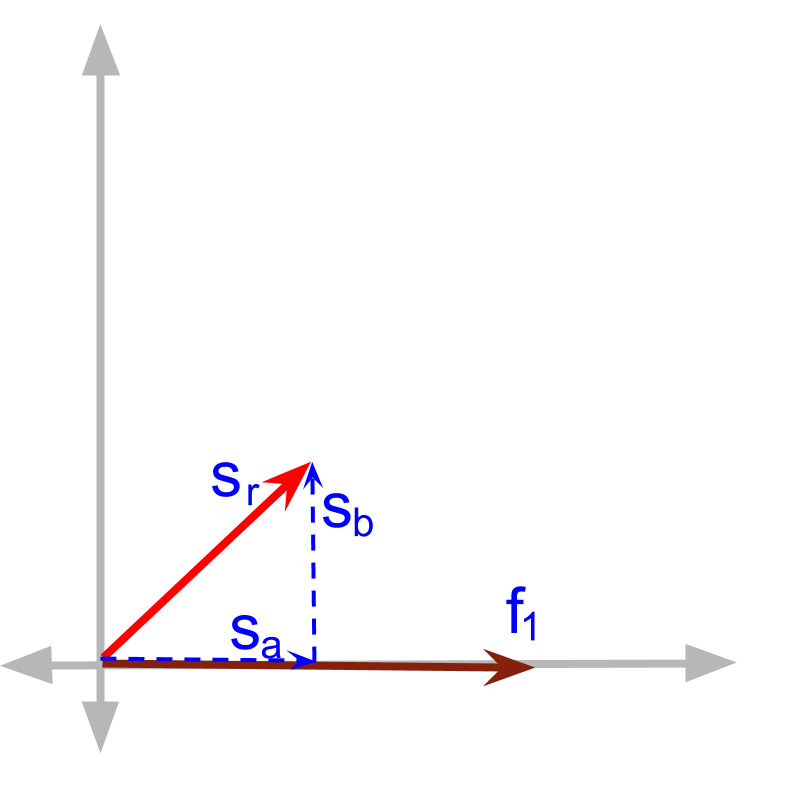
A vector can be split into components in parallel and in perpendicular directions to another vector.

Consider that force ${\vec{f}}_{1}$ $vec f_1$ is acting on an object which moves displacement ${\vec{s}}_{r}$ $vec s_r$ . The effect ${\vec{s}}_{r}$ $vec s_r$ is split into components ${\vec{s}}_{a}$ $vec s_a$ and ${\vec{s}}_{b}$ $vec s_b$ , where ${\vec{s}}_{a}$ $vec s_a$ is in the same direction as the cause ${\vec{f}}_{1}$ $vec f_1$ . The work done by cause $f_{1}$ $f_1$ is ' $f_{1}$ $f_1$ multiplied by $s_{a}$ $s_a$ ' as the effect is in the same direction and in that direction no other cause is observed.

Generalizing that... For two vectors $\vec{p}$ $vec p$ and $\vec{q}$ $vec q$ , the vector dot product of the vectors is given by multiplication of
• magnitude of one vector and
• the magnitude of the component of second vector in parallel to the first vector.

$\vec{p} \cdot \vec{q} = | p | | a |$ $vec p cdot vec q = |p| |a|$
where $| a |$ $|a|$ is the component of $\vec{q}$ $vec q$ in the direction of $\vec{p}$ $vec p$ .

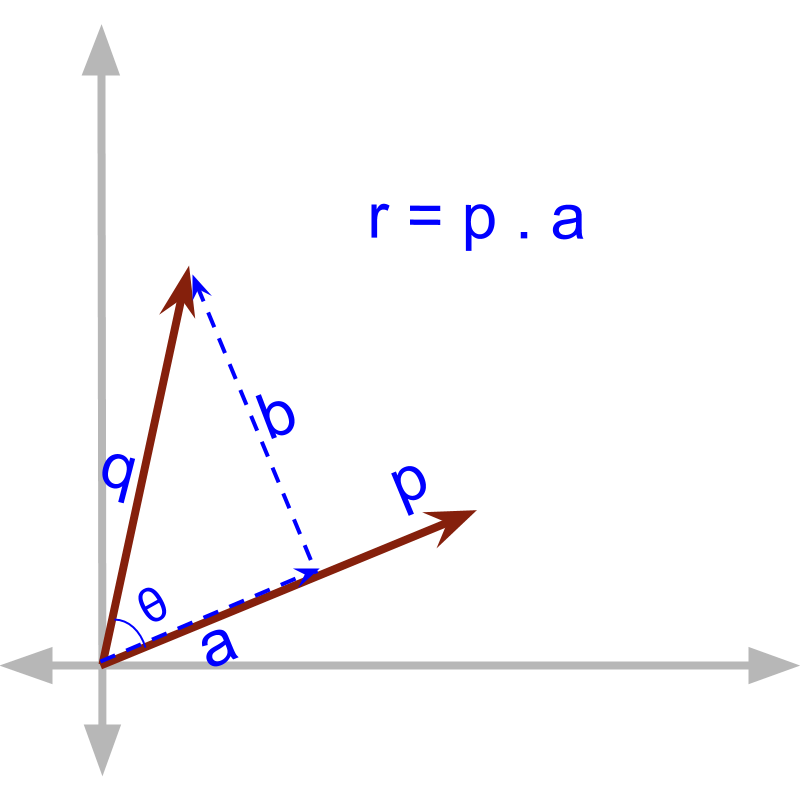
The component $a$ $a$ can be computed as ' $| q | \cos θ$ $|q|cos theta$ ', using basic trigonometry.

This product is formally defined as vector dot product.

$\vec{p} \cdot \vec{q} = | p | | q | \cos θ$ $vec p cdot vec q = |p||q|cos theta$
Note that the result is a scalar. So, this operation is also called Scalar Product of vectors.

A vector multiplication for components in parallel (in the same direction) is defined as scalar product or dot product.

The component in perpendicular does not take part in the dot product. This product of vector models application with the cause-effect relations that always in the same direction.

When two vector quantities interact to form a product, either one of the (1) component in parallel or (2) component in perpendicular is involved in the multiplication.

A vector multiplication for components in perpendicular is defined as cross product. This is explained later.

examples

Two vectors $\vec{p}$ $vec p$ and $\vec{q}$ $vec q$ with magnitudes $2$ $2$ and $3$ $3$ respectively are at an angle $60^{\circ}$ $60^@$ . What is $\vec{p} \cdot \vec{q}$ $vec p cdot vec q$ ?

$\vec{p} \cdot \vec{q}$ $vec p cdot vec q$
$= | p | | q | \cos θ$ $= |p||q|cos theta$
$= 2 \times 3 \times {\cos 60}^{\circ}$ $= 2 xx 3 xx cos 60^@$
$= 2 \times 3 \times \frac{1}{2}$ $=2 xx 3 xx 1/2$
$= 3$ $=3$

Vector with magnitudes $4$ $4$ and $6$ $6$ are in the opposite directions. What is the dot product of these two vectors?

The answer is ' $- 24$ $-24$ '. The angle between the vectors is $180^{\circ}$ $180^@$ and ${\cos 180}^{\circ} = - 1$ $cos180^@ = -1$ .

A vector $\vec{p}$ $vec p$ of magnitude $30$ $30$ is the cause. The observed effect is $\vec{q}$ $vec q$ of magnitude $20$ $20$ at an angle $45^{\circ}$ $45^@$ to the $\vec{p}$ $vec p$ . What is the product between them?

The answer is ' $300 \sqrt{2}$ $300 sqrt 2$ '. Product between cause and effect is vector dot product $| p | | q | \cos θ$ $|p||q|cos theta$ .

summary

Vector Dot Product / Scalar Product : is defined as
$\vec{p} \cdot \vec{q} = | p | | q | \cos θ$ $vec p cdot vec q = |p||q|cos theta$ where $θ$ $theta$ is the angle between $\vec{p}$ $vec p$ and $\vec{q}$ $vec q$ .

It is the product of components in parallel (i.e. in the same direction).

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed