
Vector Algebra
Welcome to the only place where the essence of vectors is explained.
• A vector in first-principles is a quantity with spatial-direction specified. Example: north-east.
• A vector in component form is linear-combination of unit vectors of independent directions. eg:
• A vector in 3D co-ordinate system is a ray initiating from the origin.
Vector addition, dot product, and cross product are explained in
» first principle,
» geometrical meaning, and
» component form.
The details explained here are revolutionary and astonishingly simple to understand.
maths > vector-algebra > vector-scalar-difference
Introducing Vectors
To completely specify and to use in mathematical calculations, some quantities require both magnitude and direction. calculations.
» Measurement of Quantities
→ Addition: sum of measured amount
→ Subtraction: difference in measured amount
» Some quantities do not add or subtract only in the amount
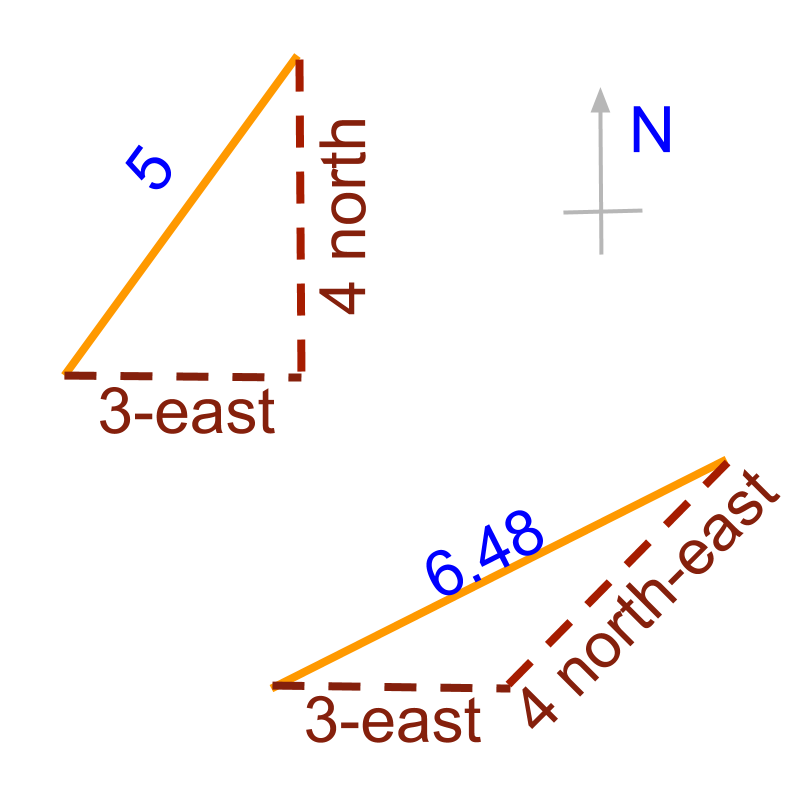 → east + north is not
→ east + north is not
→ east + north-east is approximately
» Some quantities cannot be used in calculation if only amount is given without direction
» Measurement of such quantities should capture both the amount and the direction to carryout calculations
maths > vector-algebra > representation-of-vectors
Mathematical Representation of Vectors
» Vectors specify amount or magnitude and direction
→ m east and m north
→ m east and m north-east
» How were the quantities added?
→ m east + m north = as per Pythagoras theorem
→ m east + m north-east : Making this easy to do is the objective of "vector algebra"
» Position of an airplane
→ 3Okm east (x-axis) =
→ 40km north (y-axis) =
→ 4km altitude (z-axis) = 4k
» component form of a vector
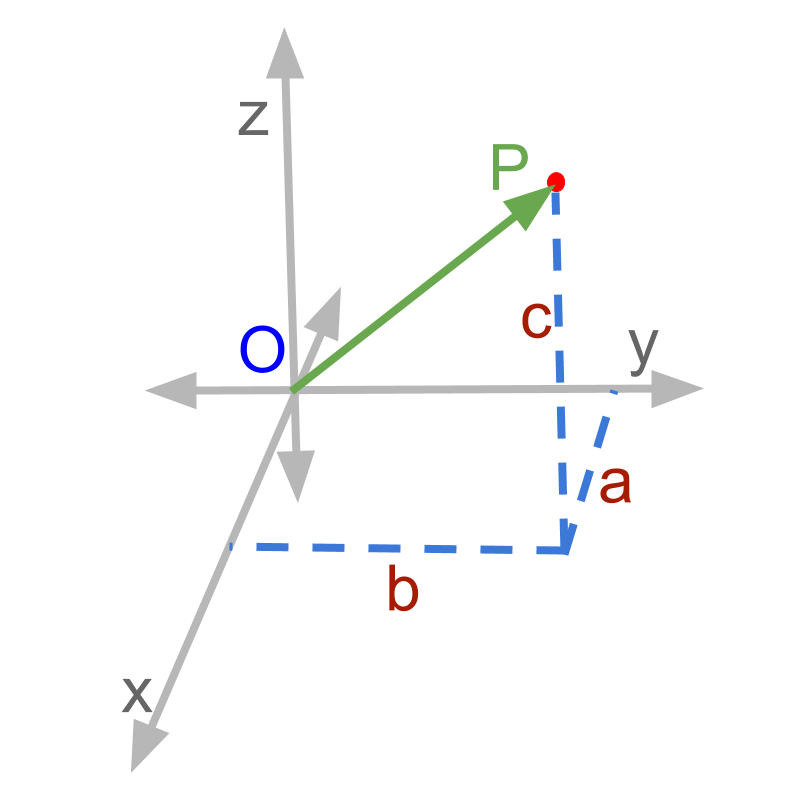 → ,, represent the direction along , , and axes
→ ,, represent the direction along , , and axes
→ , , represent the amount or magnitude along the given directions
maths > vector-algebra > magnitude-of-vector
Magnitude of a Vector
In this page, computing magnitude of a vector is explained in detail. magnitude of is
 → length of is the magnitude
→ length of is the magnitude
maths > vector-algebra > types-of-vectors
Types of Vectors
Classification of Vectors
» Classification by magnitude
→ null or zero vector : magnitude
→ unit vector : magnitude
→ proper vector : magnitude not <
» By similarities of two vectors
→ equal vectors : All corresponding components equal
→ like vectors: same directions
→ unlike vectors : different directions
→ co-initial vectors : same initial point
→ co-linear vectors : on the same line
→ co-planar vectors : on the same plane
→ non-co-planar vectors : not on the same plane
maths > vector-algebra > properties-magnitude-of-vector
Properties of Magnitude of a Vector
In this topic, Properties of Magnitude of vectors are explained in detail.
» Magnitude of null vectors
» Magnitude of a negative
» Magnitude of an unit vector
maths > vector-algebra > relationship-between-vectors-coordinate-geometry
Vector and Coordinate Geometry
In this topic, you will learn about how vector algebra can be used in coordinate geometry and how coordinate geometry principles help in vector algebra problems.
» Vector Algebra in Coordinate Geometry
→ Vector representation can be used to describe points in coordinate space.
→
→ Distance between origin and the point is the magnitude of the vector.
Vector Algebra can be used to solve probems in coordinate geometry.
» Coordinate Geometry in Vector Algebra
→ Vectors are directed line segments in coordinate space
→ Magnitude is the distance between initial and terminal points
→ Relative properties of vectors, like, angle between vectors, are preserved
Properties and results of coordinate geometry can be used to solve vector algebra problems
maths > vector-algebra > position-vector-of-a-point
Position Vector of a Point
In this page, you will learn about position vector of a point. This concept connects vector algebra and coordinate geometry.
» For a point the position vector is

maths > vector-algebra > directional-cosine-of-a-vector
Directional Cosine
In this page, you will learn about the alternate representation of vectors other than ?
Directional Cosine
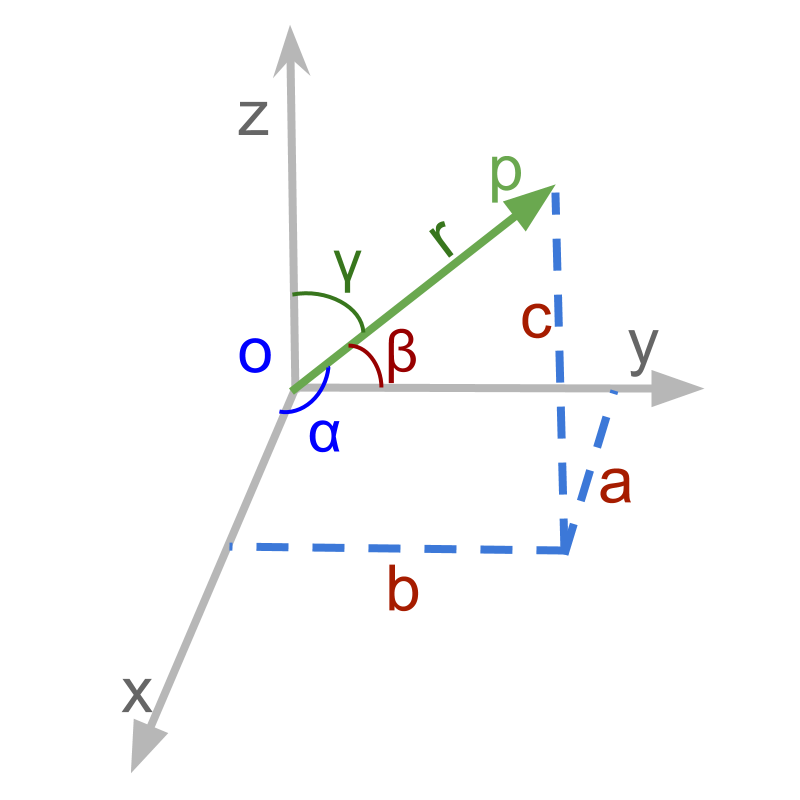 → makes angles with -axes respectively
→ makes angles with -axes respectively
→
→
→
maths > vector-algebra > introduction-vector-arithmetic
Vector Arithmetic
In this page, the basic mathematical operations of vector algebra is introduced with examples.
Vector Arithmetic
» Application Scenarios of Vector Arithmetic
→ Addition of two quantities: Two vectors can be added
→ Subtraction : inverse of addition
→ Repeated addition of a quantity: a vector is multiplied by a scalar
→ Product between two quantities : two vectors can be multiplied
» Two Possibilities of Vector Multiplication
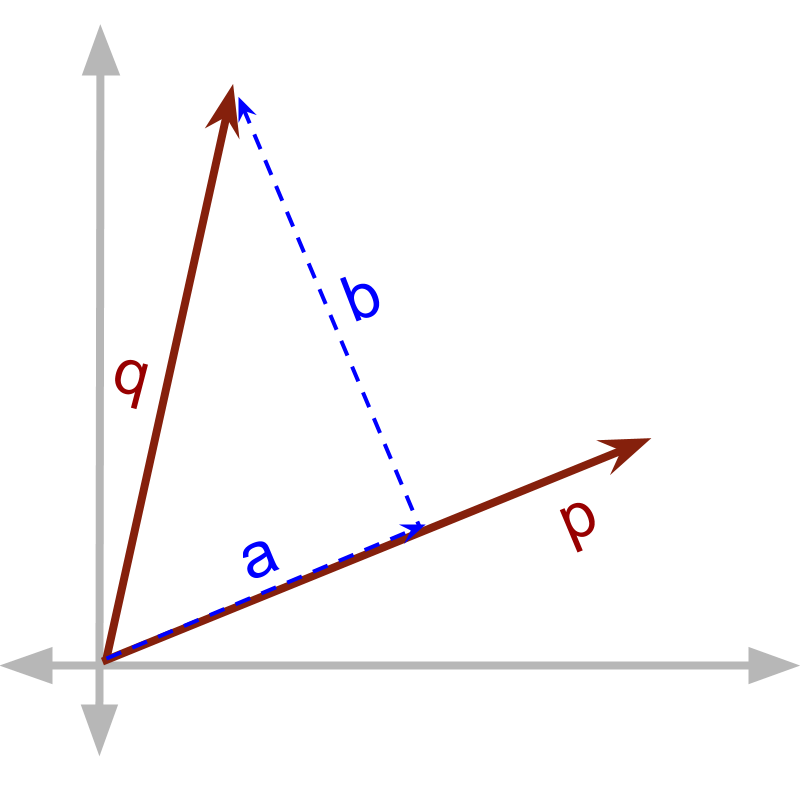
→ Vector Dot Product : multiply with component in parallel
→ Vector Cross Product : multiply with component in perpendicular
» Vector Division is not defined
→ Division is the inverse of multiplication. In vector multiplication, one of the components is lost in the product. And so vector division is not defined.
All these arithmetic operations are explained in detail later. The objective of this is to understand the role of components in parallel and in perpendicular.
maths > vector-algebra > understanding-direction-of-vectors
Understanding Direction
How the property 'direction' affects vector quantities in mathematical calculations?
Independence of Quantities along Orthogonal Directions
→ For a vector, a change along one axis affects only the component along that axis and do not affect the components along other axes, as the axes are orthogonal
» Effect of Direction:
→ Addition involves right-triangles and Pythagorean identity
→ Product between quantities involves either one of component in parallel or perpendicular
maths > vector-algebra > vector-addition-first-principles
Vector Addition - First principles
In this page, you will learn first principles of how two vectors quantities add up?
Vector Addition: First Principles
» Components in parallel add and component in perpendicular combine as right triangle
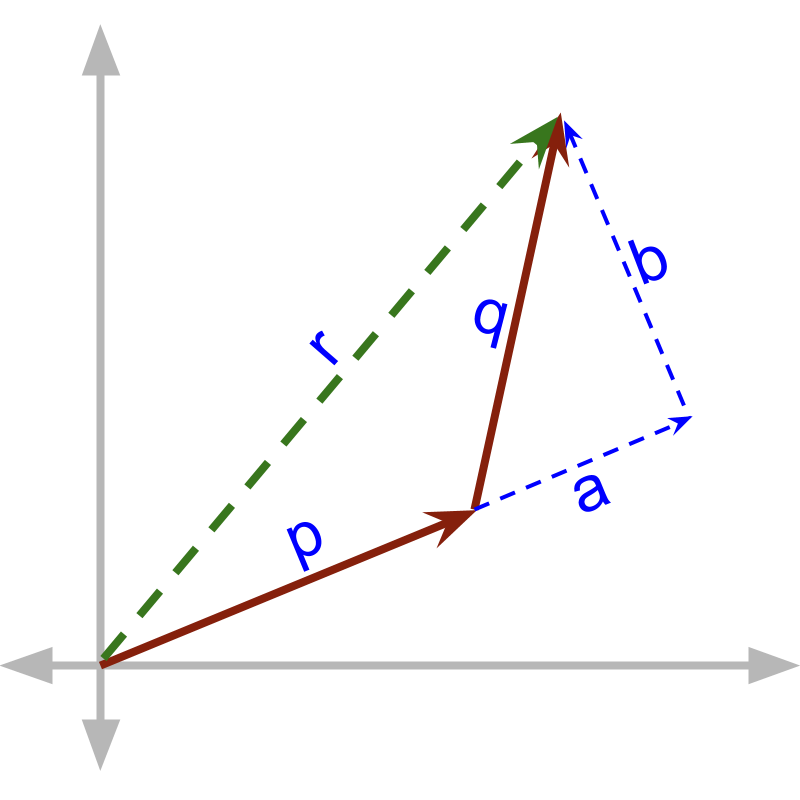 → component in parallel to is
→ component in parallel to is
→ component in perpendicuar to is
→ and result in
maths > vector-algebra > vector-addition-component-form
Vector Addition in Component form
In this page, learn how two vectors in component form add up.
» individual components add
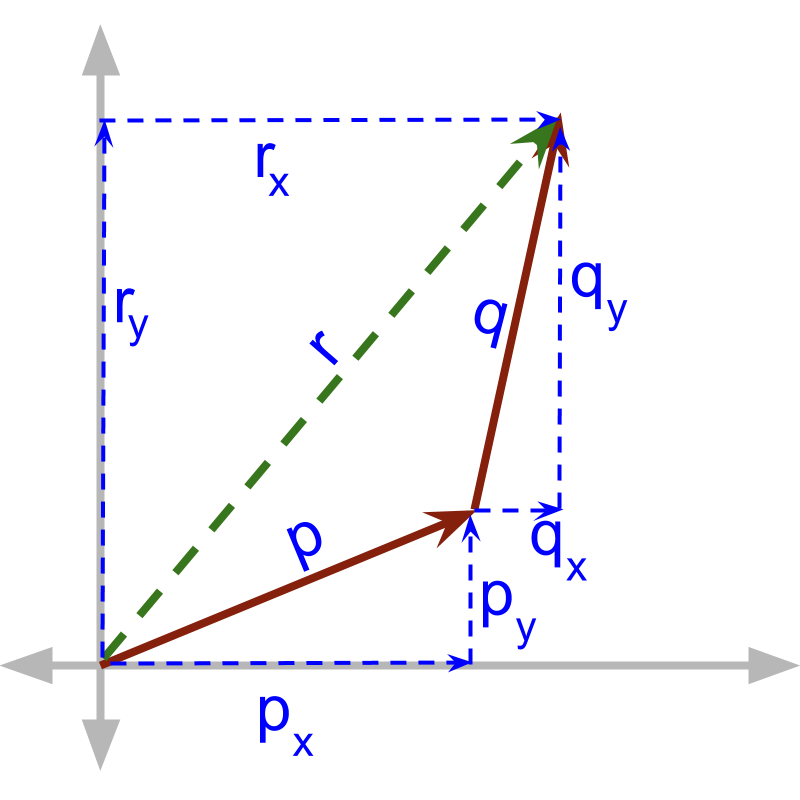 →
→
→
→
maths > vector-algebra > triangular-law-of-vector-addition
Triangular Law
In this page, the triangular law of vector addition is explained as sequential addition of vectors.
sequential addition of and
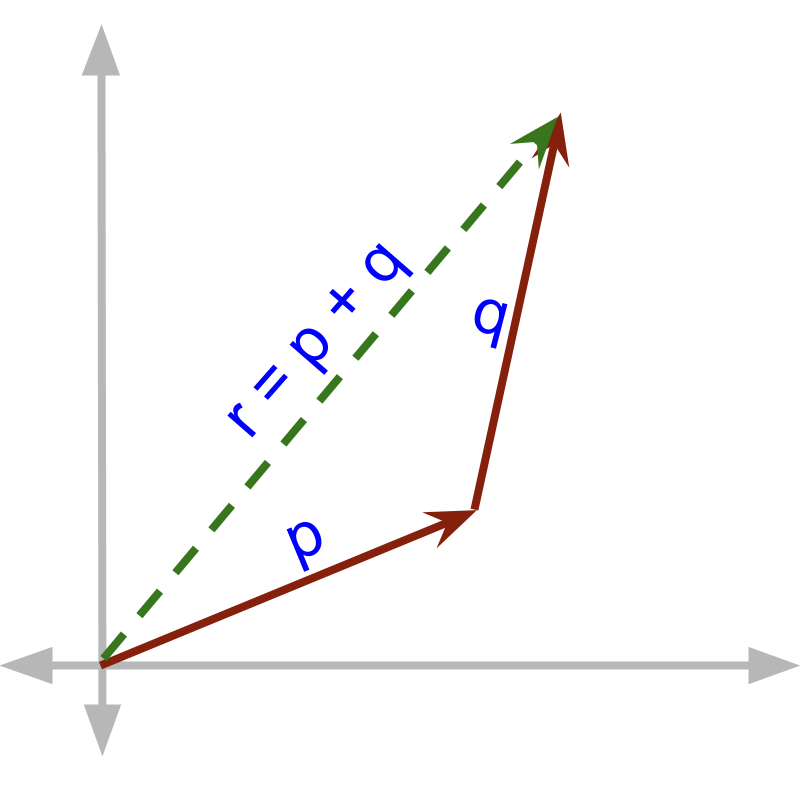 → the third side of the triangle formed by and
→ the third side of the triangle formed by and
maths > vector-algebra > parallelogram-law-of-vector-addition
Parallelogram Law
In this page, the parallelogram law of vector addition is explained as a continuous addition of vectors.
continuous addition of and
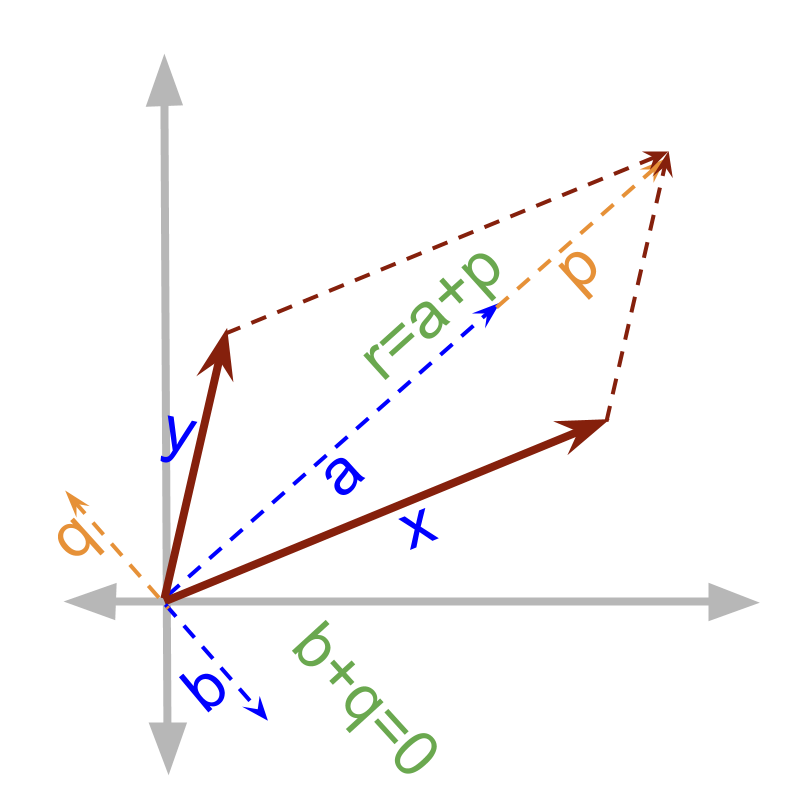 →
→
→
→ the co-initial diagonal of the parallelogram formed by sides and
maths > vector-algebra > repeated-addition
Repeated addition of a Vector
In this page repeated addition of vectors is explained.
» Repeated addition is generalized to Multiplication of a vector by Scalar
» Components are multiplied by scalar
→
→
maths > vector-algebra > standard-unit-vectors
Standard Unit Vectors
In this page, orthogonal axes of vector space and the standard unit vectors are explained.
» orthogonal axes are represented with unit vectors
→ x-axis
→ y-axis
→ z-axis
maths > vector-algebra > vector-as-sum-of-vectors
Vector as sum of vectors
In this page, you will learn that Vectors can be represented as sum of several vectors.
» Vectors as Linear combination of vectors
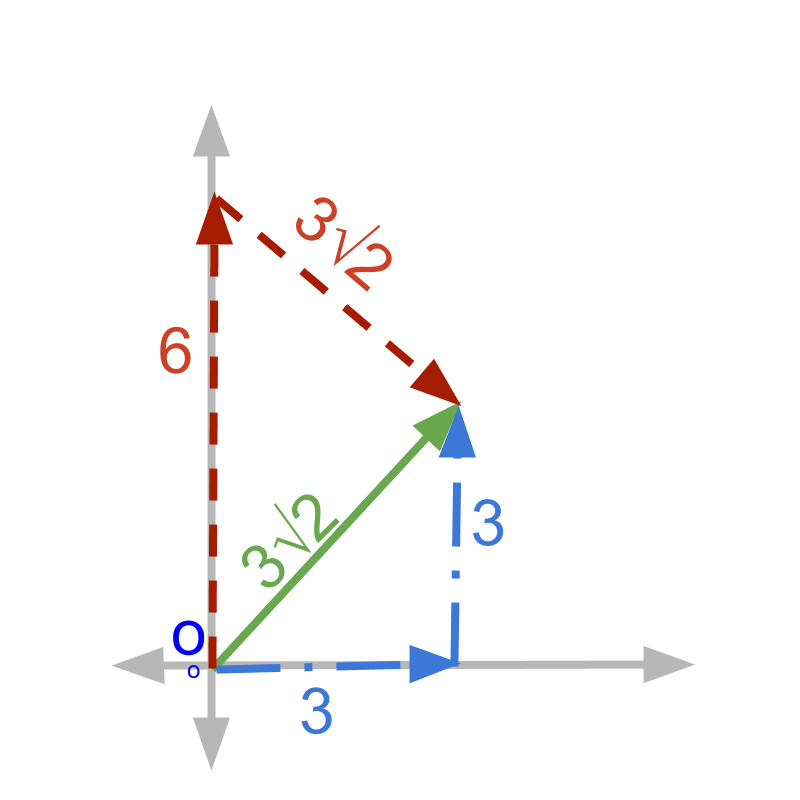 → at angle
→ at angle
→ at + at
→ at + at
All these represent the same vector.
maths > vector-algebra > vector-component-form
Component form of Vectors
Vectors are represented in component form as sum of standard unit vectors multiplied by scalars.
Vector Component Form is linear combination of vectors
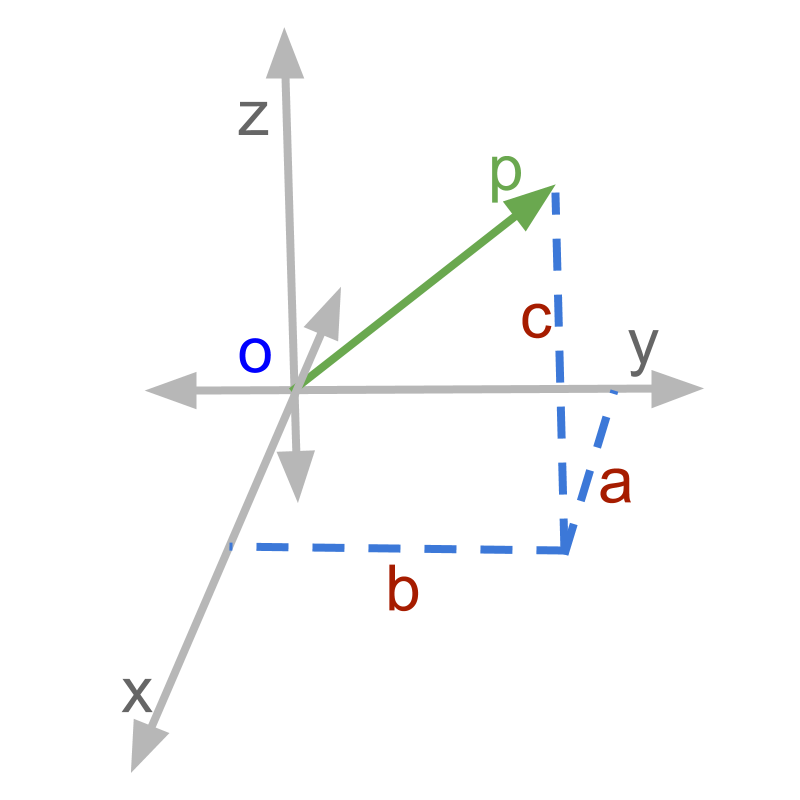 → , , are unit vectors
→ , , are unit vectors
→ , , are scalars
→
component form is scalar multiplication and addition of unit vectors.
maths > vector-algebra > introducing-multiplication-of-vectors
Multiplication of Vectors
In this page, learn in detail about basics of 'vector multiplication'.
» Two products because of orthogonality of components of vectors
 → dot product is defined for components in parallel
→ dot product is defined for components in parallel
→ cross product is defined for components in perpendicular
maths > vector-algebra > vectors-cause-effect-relation
Cause-Effect relation
In this page, the primary application of vector dot product "cause-effect relations" is explained. » Two vectors that are cause-effect relation will be in same direction
→ is the cause
→ is the effect of the cause
→ both and will be in same direction » Dot product is defined for applications with product involving cause-effect relation
» Note: the dot product is used in applications where parallel components take part in multiplication
maths > vector-algebra > vectors-scalar-dot-product-first-principles
Vector Dot Product : First Principles
In this page, the vector dot product is explained in first principles.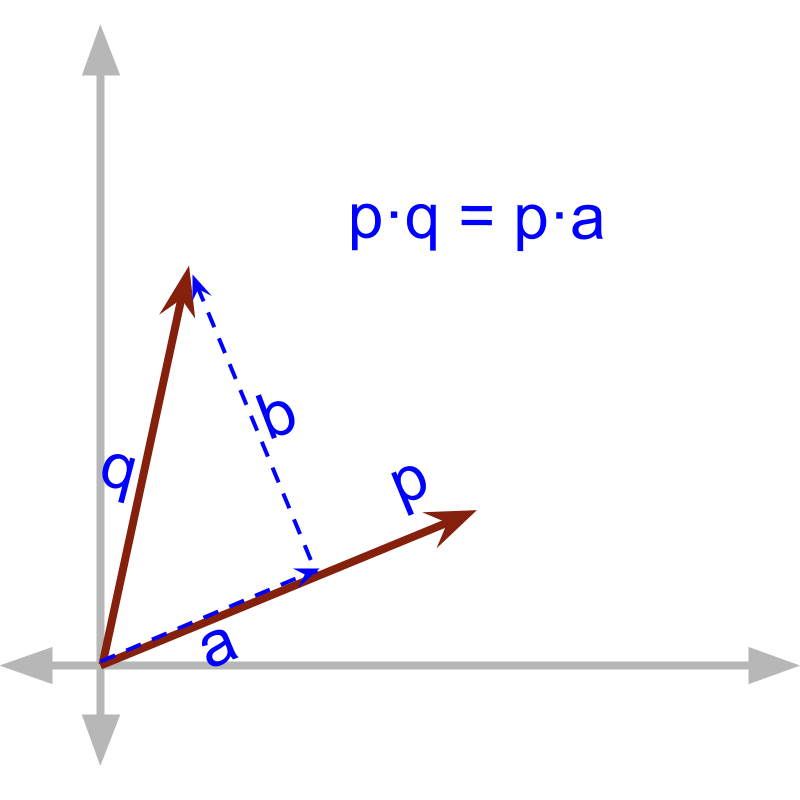 →
→
→ product of magnitudes of components in parallel
maths > vector-algebra > dot-product-projection-form
Vector Dot Product : Projection of a vector
In this page, you will learn about computing projection of vector using vector dot product.
» component in parallel is calculated by the angle
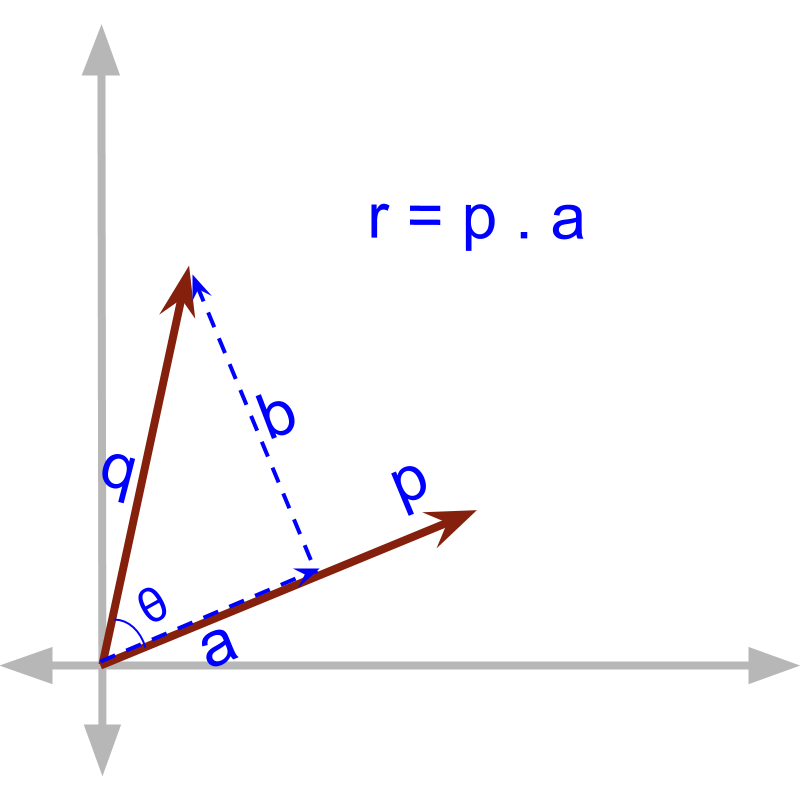 →
→
→ Note that
→ is the projection of on
maths > vector-algebra > dot-product-component-form
Vector Dot Product : Component Form
In this page, you will learn about the component form of the vector dot product.
» sum of product of individual components
→
maths > vector-algebra > dot-product-with-added-direction
Dot product with Added Direction
In this page, learn about adding direction to the scalar product with an example.
» By definition, dot product is scalar
» Some applications may specify an additional direction in the multiplication of components in parallel. In such cases, the direction is combined.
maths > vector-algebra > introduction-cross-product
Introduction to Cross Product
In this page, learn in detail about basics of 'vector cross product' with an example.
» Two products because of orthogonality of components of vectors
 → dot product is defined for components in parallel
→ dot product is defined for components in parallel
→ cross product is defined for components in perpendicular
maths > vector-algebra > vector-cross-product-first-principles
Cross Product: First Principles
In this page, the vector cross product is explained in first principles.
» multiplied with component in perpendicular
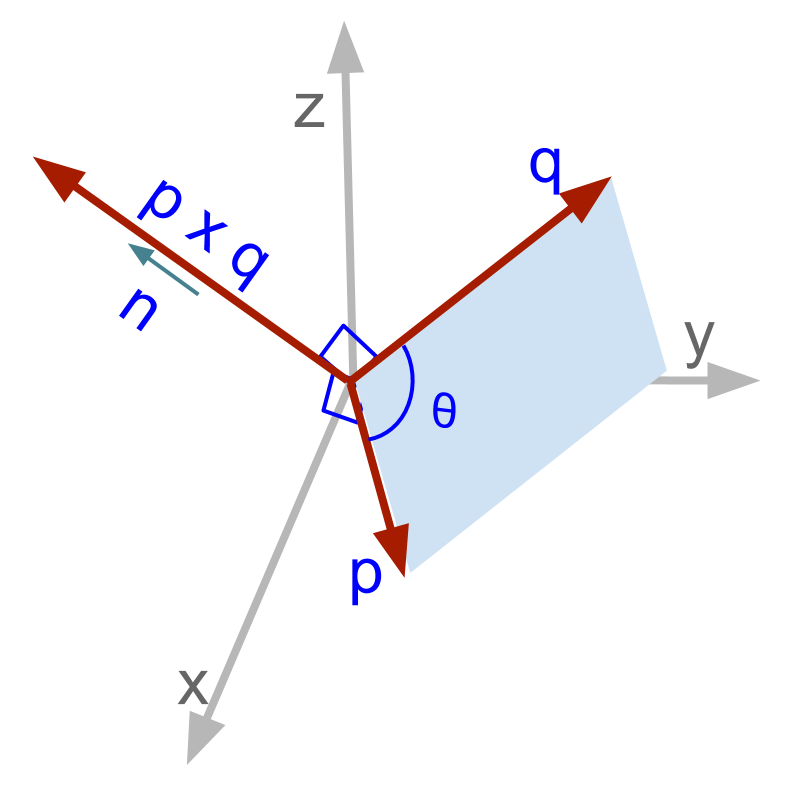 →
→
→ product of magnitudes of components in perpendicular
→ direction perpendicular to both the vectors
maths > vector-algebra > cross-product-area-of-parallelogram
Cross Product : Area of Parallelogram
In this page, you will learn about computing area of a parallelogram using vector cross product.
» component in perpendicular is calculated by the angle
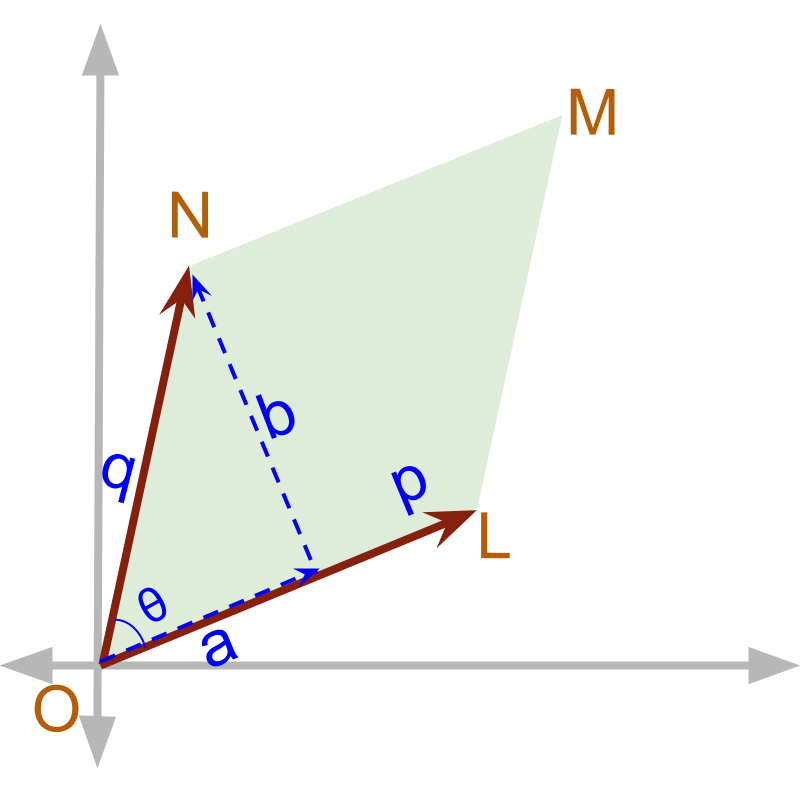 →
→
→ Note that
→ is the area of parallelogram with sides and
maths > vector-algebra > vector-cross-product-component-form
Cross Product: Component Form
In this page, you will learn about the component form of the vector cross product.
maths > vector-algebra > cross-product-with-direction-removed
Cross Product with Direction removed
In this page, you will learn about removing the direction of the vector cross product with an example application.