Vector Algebra : Dot product with Added Direction

maths > vector-algebra

Dot product with Added Direction

what you'll learn...

Overview

Dot Product with Added Direction

» By definition, dot product is scalar

» Some applications may specify an additional direction in the multiplication of components in parallel. In such cases, the direction is combined.

think different

An object by position vector $\vec{p}$ $vec p$ casts a shadow on a screen. The screen in given by unit vector $\vec{s}$ $vec s$ . The shadow is a vector that spans as a ray with a starting and end point.

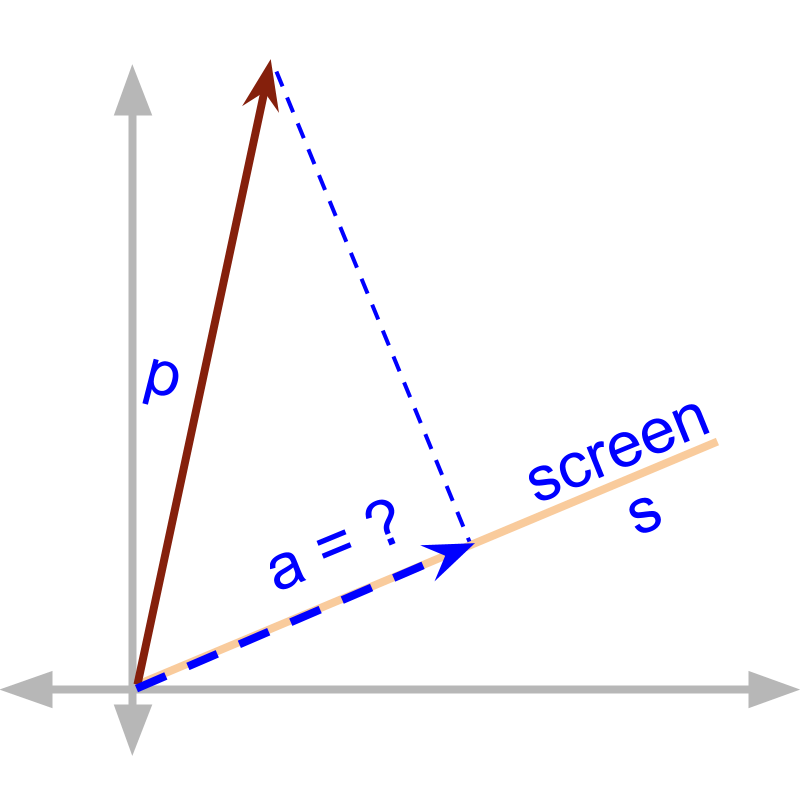
$\vec{p}$ $vec p$ and the screen $\hat{s}$ $hat s$ are given. The length of the shadow is $\vec{p} \cdot \hat{s}$ $vec p cdot hat s$ which is a scalar $| p | \cos θ$ $|p| cos theta$

The shadow is a vector along the direction of $\hat{s}$ $hat s$ and the length of the shadow is $\vec{p} \cdot \hat{s}$ $vec p cdot hat s$ . Combining thest to the shadow is given as $(\vec{p} \cdot \hat{s}) \hat{s}$ $(vec p cdot hat s) hat s$

summary

Projection vector using Dot Product: For a vector $\vec{p}$ $vec p$ and a direction given by unit vector $\hat{s}$ $hat s$ , the projection vector of $\vec{p}$ $vec p$ in direction $\hat{s}$ $hat s$ is $(\vec{p} \cdot \hat{s}) \hat{s}$ $(vec p cdot hat s) hat s$ .

Vector dot product by definition is a scalar. Depending on the application requirement, a direction can be added to the scalar.

Outline

The outline of material to learn vector-algebra is as follows.

Note: Click here for detailed outline of vector-algebra.

• Introduction to Vectors

→ Introducing Vectors

→ Representation of Vectors

• Basic Properties of Vectors

→ Magnitude of Vectors

→ Types of Vectors

→ Properties of Magnitude

• Vectors & Coordinate Geometry

→ Vectors & Coordinate Geometry

→ Position Vector of a point

→ Directional Cosine

• Role of Direction in Vector Arithmetics

→ Vector Arithmetics

→ Understanding Direction of Vectors

• Vector Addition

→ Vector Additin : First Principles

→ Vector Addition : Component Form

→ Triangular Law

→ Parallelogram Law

• Multiplication of Vector by Scalar

→ Scalar Multiplication

→ Standard Unit Vectors

→ Vector as Sum of Vectors

→ Vector Component Form

• Vector Dot Product

→ Introduction to Vector Multiplication

→ Cause-Effect-Relation

→ Dot Product : First Principles

→ Dot Product : Projection Form

→ Dot Product : Component Form

→ Dot Product With Direction

• Vector Cross Product

→ Vector Multiplication : Cross Product

→ Cross Product : First Principles

→ Cross Product : Area of Parallelogram

→ Cross Product : Component Form

→ Cross Product : Direction Removed