
what you'll learn...
Overview
Vector Cross Product: Component Form
in component form
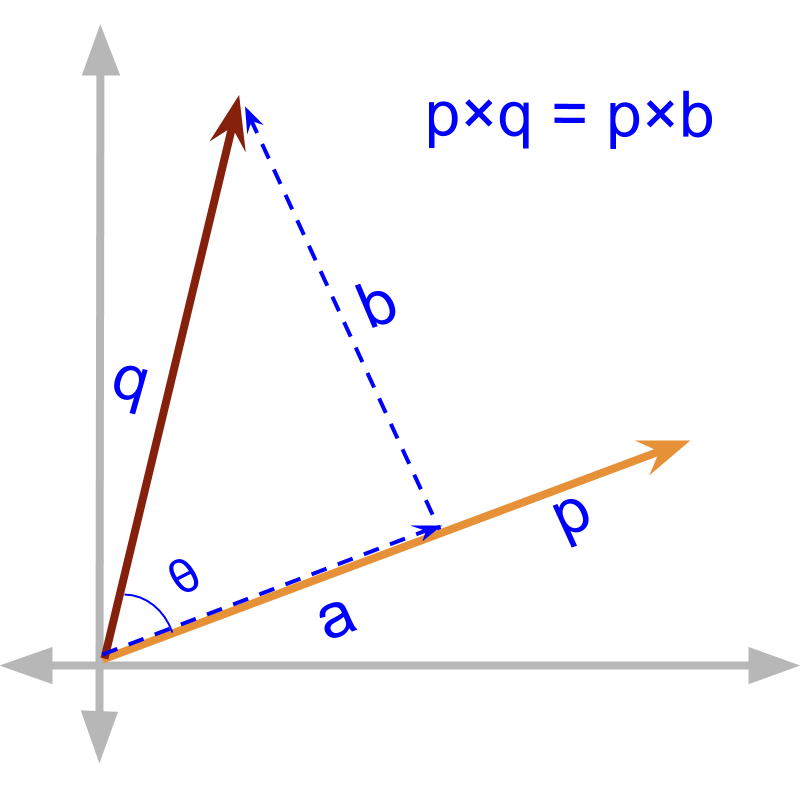
Given and and
How to find , or the cross product in the component form?
Component form of vector cross product : geometrical proof
Substitute the following
and after some algebraic rearrangement, the following is arrived at
It is proven that
The same can be written in the determinant form
easier proof
The proof given above is complex. A simpler proof, that a student can easily derive, is given below.
Bilinear Property: For any vector and
This is explained and proven in properties of the cross product. For now, consider this to be true.
A vector is sum of scalar multiple of vectors. are unit vectors, and the scalar multiples are .
The same applies to -- sum of multiple of vectors.
Proof for component form of vector cross product using bilinear property of cross product.
Applying bilinear property of cross product
Applying , ,
, ,
, ,
After algebraic rearrangement, we get
summary
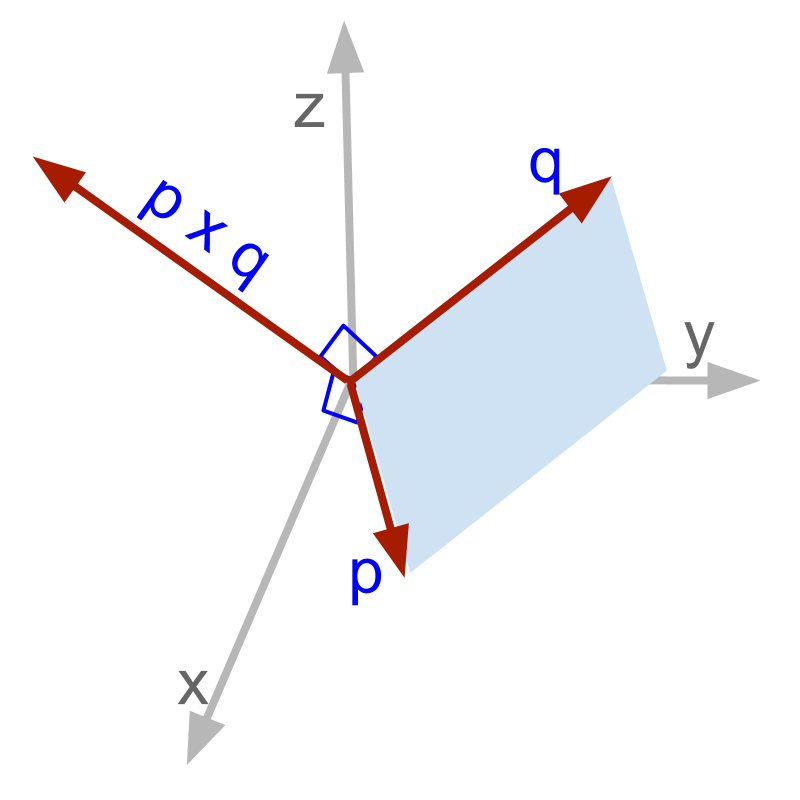
Vector Cross Product: for vectors
Vector Cross Product between two vectors in component form is defined as a vector from a determinant.
Outline
The outline of material to learn vector-algebra is as follows.
Note: Click here for detailed outline of vector-algebra.
• Introduction to Vectors
→ Introducing Vectors
→ Representation of Vectors
• Basic Properties of Vectors
→ Magnitude of Vectors
→ Types of Vectors
→ Properties of Magnitude
• Vectors & Coordinate Geometry
→ Vectors & Coordinate Geometry
→ Position Vector of a point
→ Directional Cosine
• Role of Direction in Vector Arithmetics
→ Vector Arithmetics
→ Understanding Direction of Vectors
• Vector Addition
→ Vector Additin : First Principles
→ Vector Addition : Component Form
→ Triangular Law
→ Parallelogram Law
• Multiplication of Vector by Scalar
→ Scalar Multiplication
→ Standard Unit Vectors
→ Vector as Sum of Vectors
→ Vector Component Form
• Vector Dot Product
→ Introduction to Vector Multiplication
→ Cause-Effect-Relation
→ Dot Product : First Principles
→ Dot Product : Projection Form
→ Dot Product : Component Form
→ Dot Product With Direction
• Vector Cross Product
→ Vector Multiplication : Cross Product
→ Cross Product : First Principles
→ Cross Product : Area of Parallelogram
→ Cross Product : Component Form
→ Cross Product : Direction Removed