Mensuration : Length, Area, and Volume : Perimeter & Area: Square, Rectangle, Triangle, Polygons

maths > mensuration-high

Perimeter & Area: Square, Rectangle, Triangle, Polygons

what you'll learn...

Overview

Finding perimeter and area of simple figures (squares, rectangle, triangle, polygon) are revised without much discussion.

perimeter

The word "perimeter" means: measure around a shape. Perimeter is from the Greek root words peri (around) and meter (measure).

Length is the distance-span between two points.

Perimeter :
Perimeter of a figure is the length of the line or curve forming the boundary of the figure.

Perimeter of square $= 4 \times side$ $=4 xx text( side)$

Perimeter of rectangle $= 2 \times length + width$ $=2 xx text( length + width)$

Perimeter of triangle $= sum of three sides$ $=text( sum of three sides)$

Perimeter of polygon $= sum of sides$ $=text( sum of sides)$

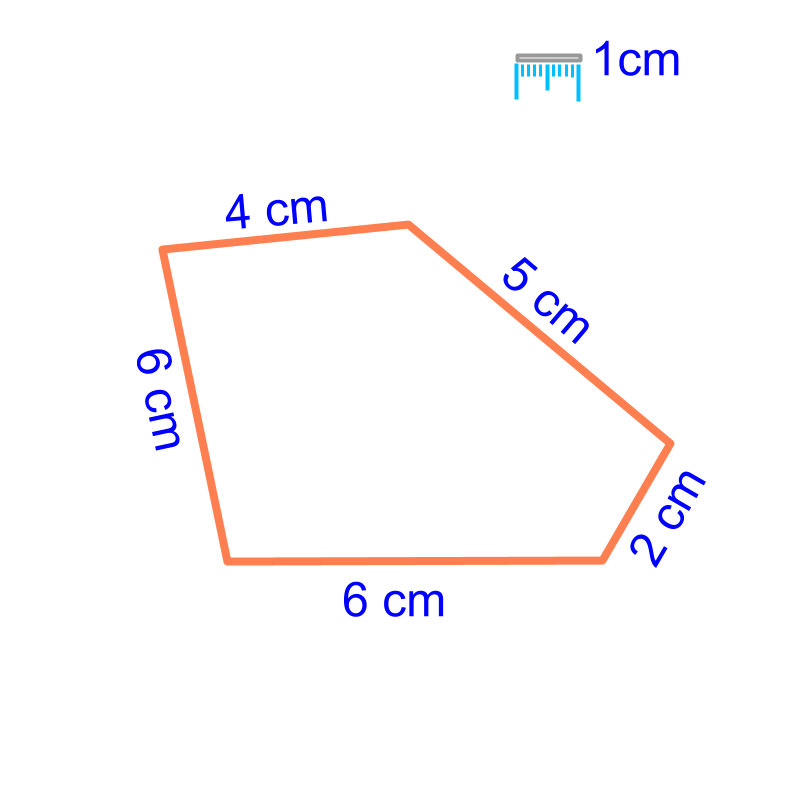
area

Area of a figure is the "surface-span within a closed shape".

Area of a Square and a Rectangle :
Area of square $= {side}^{2}$ $=text( side)^2$

Area of rectangle $= length \times width$ $=text( length ) xx text( width)$

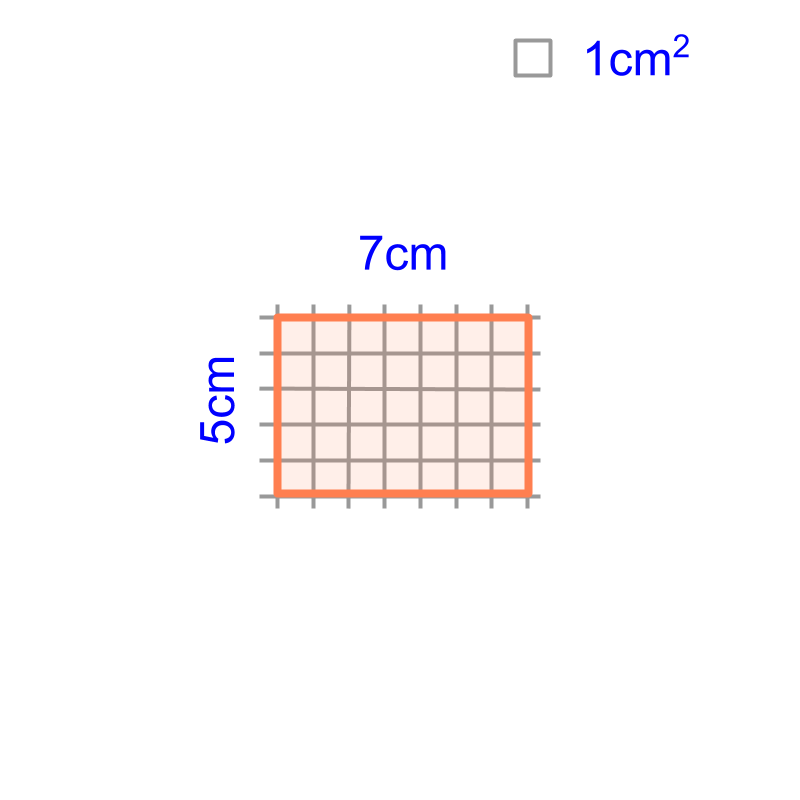
Area of a Triangle:
$\frac{1}{2} \times base \times (h e i g h t)$ $1/2 xx text( base ) xx ( height)$

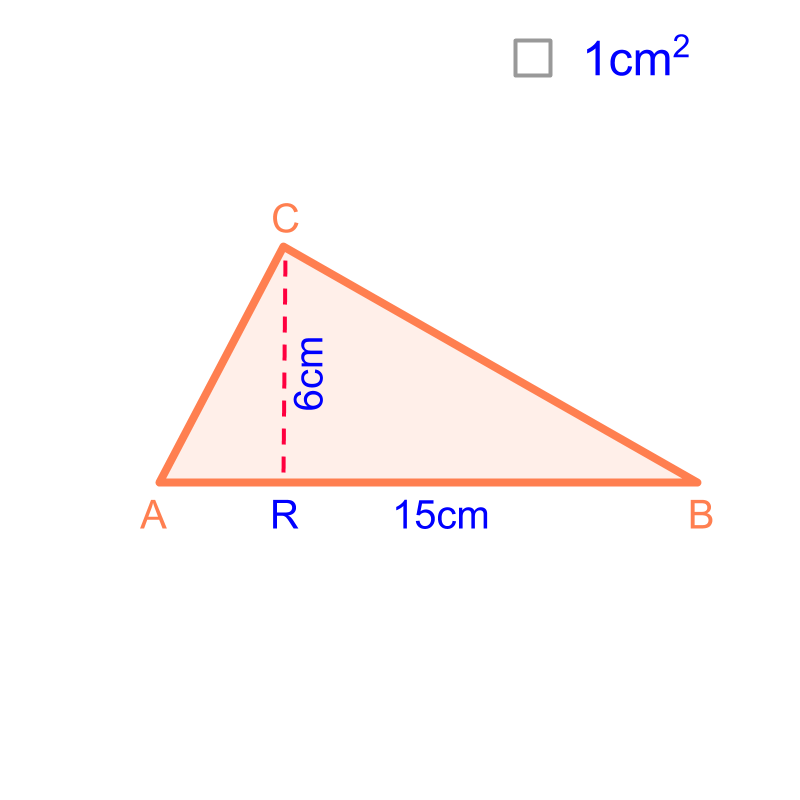
Area of a Polygon : Consider a polygon to be combination of known geometrical forms, mostly triangles.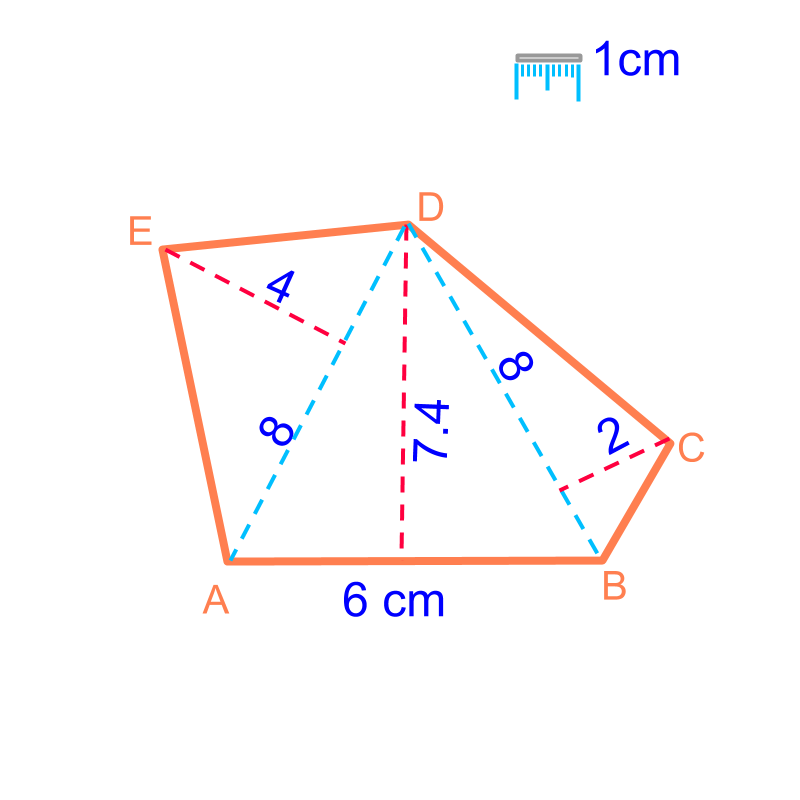 The geometrical forms and the formula for area are:

Area of a triangle $= \frac{1}{2} \times base \times height$ $= 1/2 xx text( base ) xx text( height)$

Area of a trapezium $= \frac{1}{2} \times sum of bases \times height$ $= 1/2 xx text( sum of bases ) xx text( height)$

Area of a parallelogram $= base \times height$ $= text( base ) xx text( height)$

Area of a kite $= \frac{1}{2} \times major-diagonal \times minor-diagonal$ $= 1/2 xx text( major-diagonal ) xx text( minor-diagonal)$

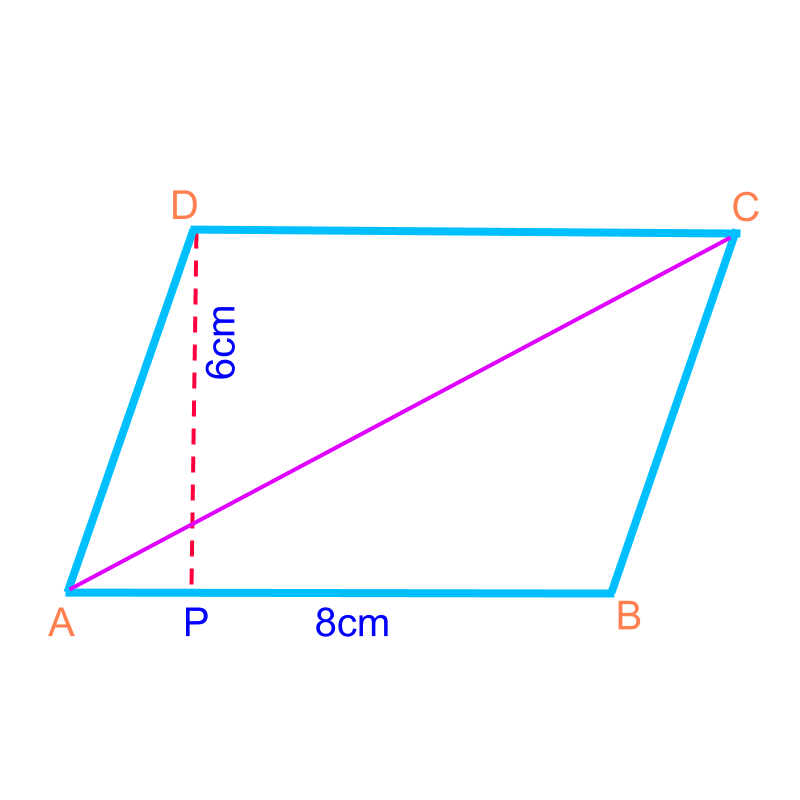
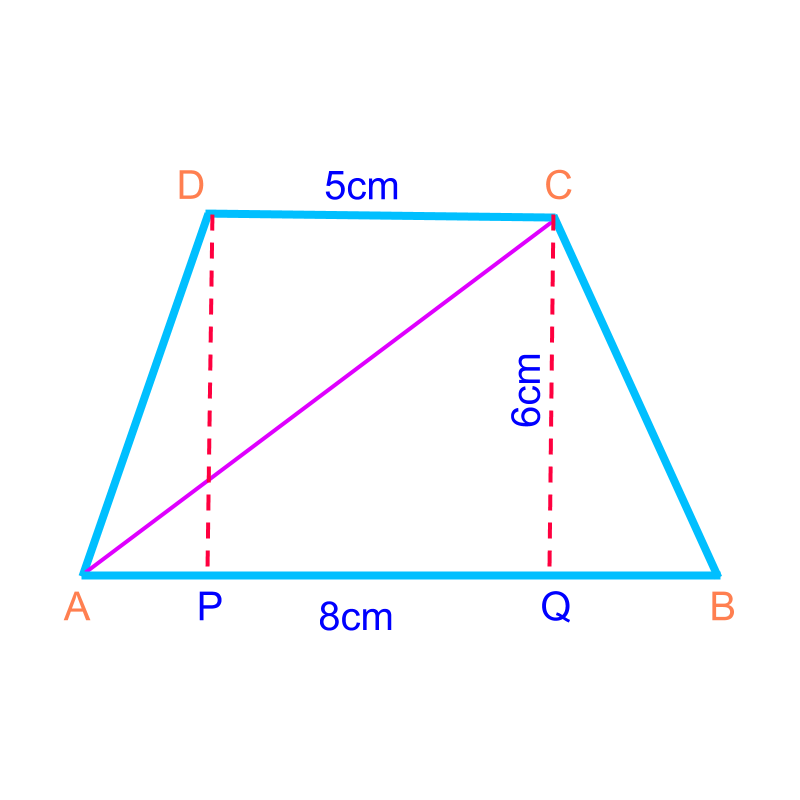
Area of Some Quadrilaterals : Consider the polygon shapes as combination of triangles and find sum of area of the triangles. 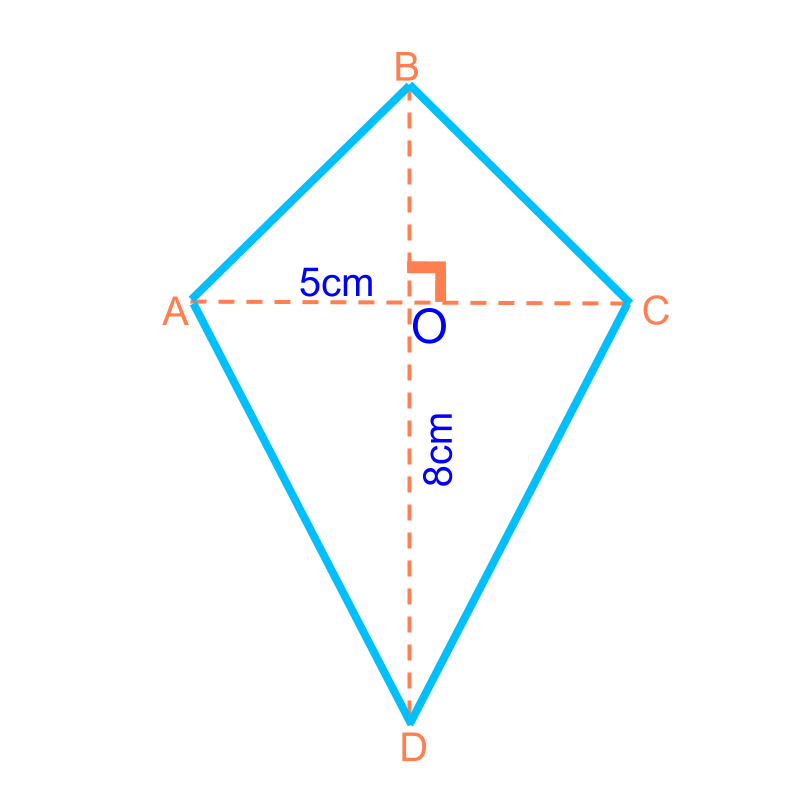area of parallelogram $area of a parallelogram$ $text( area of a parallelogram )$ $= base \times height$ $= text( base ) xx text( height)$ area of trapezium $area of a trapezium$ $text( area of a trapezium )$ $= \frac{1}{2} \times sum of bases \times height$ $= 1/2 xx text( sum of bases ) xx text( height)$ area of kite $area of a kite$ $text( area of a kite )$ $= \frac{1}{2} \times product of the diagonals$ $= 1/2 xx text( product of the diagonals)$

summary

This is covered in Mesuration-Basics in the following pages

→ Perimeter of Polygons

→ Area of Square & rectangle

→ Area of Triangle

→ Area of Polygons

→ Perimeter & Area of Quadrilaterals

Outline

The outline of material to learn Mensuration : Length, Area, and Volume is as follows.

Note 1: click here for the detailed overview of Mensuration High

Note 2: click here for basics of mensuration, which is essential to understand this.

• Basics of measurement

→ Summary of Measurement Basics

→ Measurement by superimposition

→ Measurement by calculation

→ Measurement by equivalence

→ Measurement by infinitesimal pieces

→ Cavalieri's Principle (2D)

→ Cavalieri's Principle (3D)

• Perimeter & Area of 2D shapes

→ Circumference of Circles

→ Area of Circles

• Surface area & Volume of 3D shapes

→ Prisms : Surface Area & Volume

→ Pyramids : Surface Area & Volume

→ Cone : Surface Area & Volume

→ Sphere : Surface Area & Volume

• Part Shapes

→ Understanding part Shapes

→ Circle : Sector and Segment

→ Frustum of a Cone