illustrating a problem

Consider the solid given in the figure. It consists of four flat surfaces in the front, top, back, and bottom. And a pyramidal projection on the right. A similar pyramidal hollow-space on the left.

Spend some time to visualize this.

working out equivalence

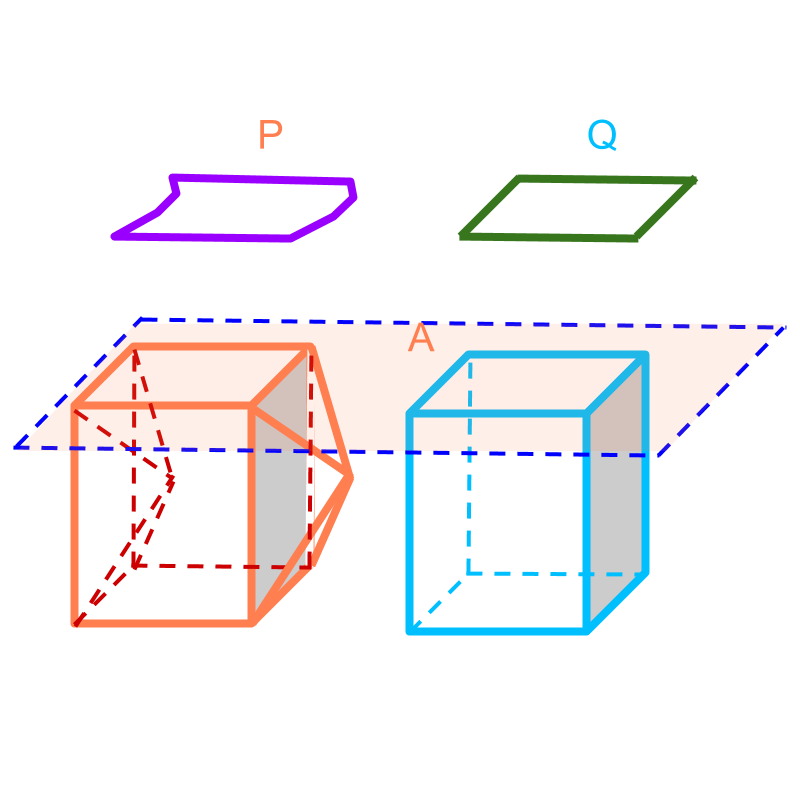
Consider finding volume of the solid given in the figure. The solid is given in orange on the left. Another solid, a cuboid, is considered. The cuboid is shown in blue.

The two figures are aligned and a plane `A` intersecting them is drawn. The intersecting plane creates two plane-figures in the two solids at the cross-section. The two plane-figures are given as `P` and `Q`.

It is noted that the area of plane-figures are equal (by Cavalieri's principle in 2D).

As per Cavalieri's principle, if the areas of the cross-sections are equal for any plane parallel to the one shown, then the volume of the two solids are equal.

This implies that "the volume of the solid equals the volume of the cuboid".

Outline

The outline of material to learn Mensuration : Length, Area, and Volume is as follows.

Note 1: click here for the detailed overview of Mensuration High

Note 2: click here for basics of mensuration, which is essential to understand this.

•  Basics of measurement

  →   Summary of Measurement Basics

  →   Measurement by superimposition

  →   Measurement by calculation

  →   Measurement by equivalence

  →   Measurement by infinitesimal pieces

  →   Cavalieri's Principle (2D)

  →   Cavalieri's Principle (3D)

•  Perimeter & Area of 2D shapes

  →   Circumference of Circles

  →   Area of Circles

•  Surface area & Volume of 3D shapes

  →   Prisms : Surface Area & Volume

  →   Pyramids : Surface Area & Volume

  →   Cone : Surface Area & Volume

  →   Sphere : Surface Area & Volume

•  Part Shapes

  →   Understanding part Shapes

  →   Circle : Sector and Segment

  →   Frustum of a Cone
next