Mensuration : Length, Area, and Volume : Measurement by Equivalence

maths > mensuration-high

Measurement by Equivalence

what you'll learn...

Overview

Measurement by Equivalence: Length, Area, or Volume can be measured by constructing an equivalent shape or object involving geometrical principles. area by equivalence

consider a problem

Consider the shape given in the figure. It is a parallelogram of base $b$ $b$ centimeter and height $h$ $h$ centimeter. To find the area of the parallelogram, the grid of unit squares is superimposed and the number of unit squared are counted. Since unit-squares will not fit exactly at the vertices, only approximate area can be computed.

equivalence

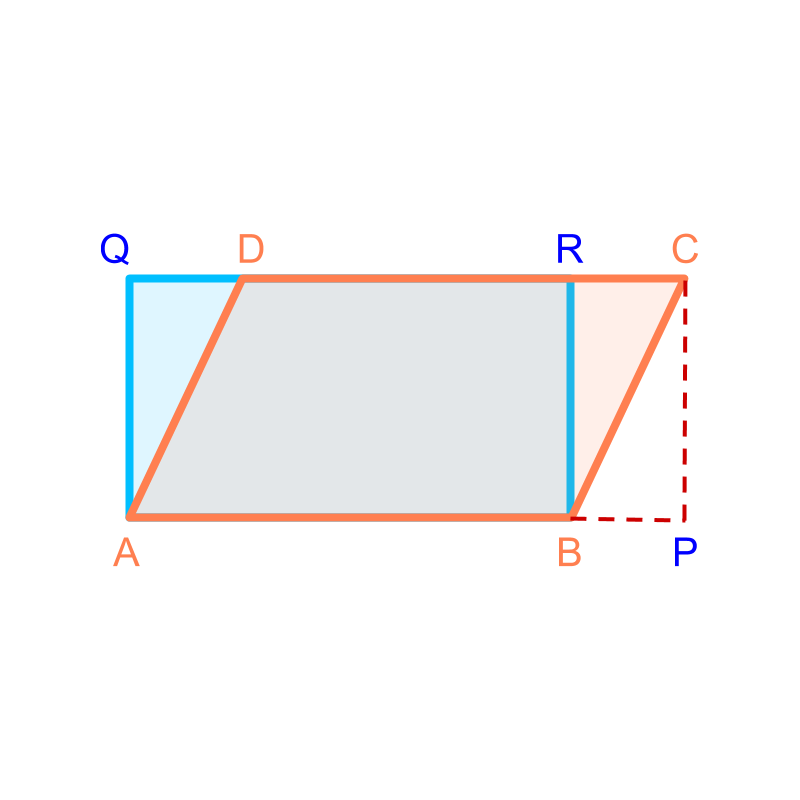
A rectangle $A B R Q$ $ABRQ$ of length $b$ $b$ cm and width $h$ $h$ cm is shown in blue. Consider the region $△ B R C$ $/_\ BRC$ and the region $△ A Q D$ $/_\ AQD$ . The area of these two triangles are equal.

The area of the parallelogram is sum of areas of the region $A B R D$ $ABRD$ and $△ B R C$ $/_\ BRC$ . This can be equivalently given as sum of areas of the region $A B R D$ $ABRD$ and $△ A Q D$ $/_\ AQD$ .

This implies that "area of the parallelogram equals the area of the rectangle".

summary

Measurement by Equivalence: Length, Area, or Volume can be measured by constructing an equivalent shape or object involving geometrical principles. area by equivalence This method suits best for

• area of plane figures of curved sides or curved surfaces

• volume of solid figures of curved edges or curved faces

Outline

The outline of material to learn Mensuration : Length, Area, and Volume is as follows.

Note 1: click here for the detailed overview of Mensuration High

Note 2: click here for basics of mensuration, which is essential to understand this.

• Basics of measurement

→ Summary of Measurement Basics

→ Measurement by superimposition

→ Measurement by calculation

→ Measurement by equivalence

→ Measurement by infinitesimal pieces

→ Cavalieri's Principle (2D)

→ Cavalieri's Principle (3D)

• Perimeter & Area of 2D shapes

→ Circumference of Circles

→ Area of Circles

• Surface area & Volume of 3D shapes

→ Prisms : Surface Area & Volume

→ Pyramids : Surface Area & Volume

→ Cone : Surface Area & Volume

→ Sphere : Surface Area & Volume

• Part Shapes

→ Understanding part Shapes

→ Circle : Sector and Segment

→ Frustum of a Cone