Mensuration : Length, Area, and Volume : Measurement by superimposition

maths > mensuration-high

Measurement by superimposition

what you'll learn...

Overview

Measurement by Superimposition : Length, Area, or Volume can be measured by superimposition of corresponding unit-measures. area by superimposition

overlay a grid

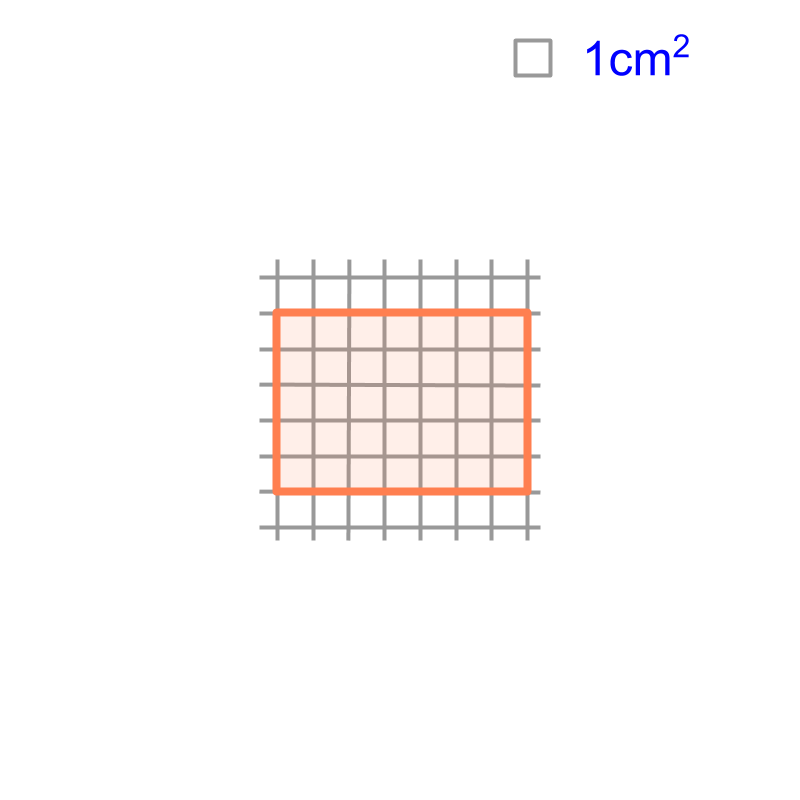
Consider the shape given in the figure. It is a rectangle of length $7$ $7$ cm and width $5$ $5$ cm. area by superimposition The figure also provides the reference unit-square on the top-right. The area of the shape is " $35 c m^{2}$ $35cm^2$ ". The area is computed by creating a grid of unit-squares. The number of unit squares contained within the shape is the area of the rectangle.

simplify

Area of the given shape is calculated by superimposing the reference unit-squares. Based on this, the area of a square or rectangle is simplified to the formulas

$Area of a square = {side}^{2}$ $text(Area of a square ) = text( side)^2$

$Area of a rectangle = length \times width$ $text(Area of a rectangle ) = text( length ) xx text( width)$

approximate

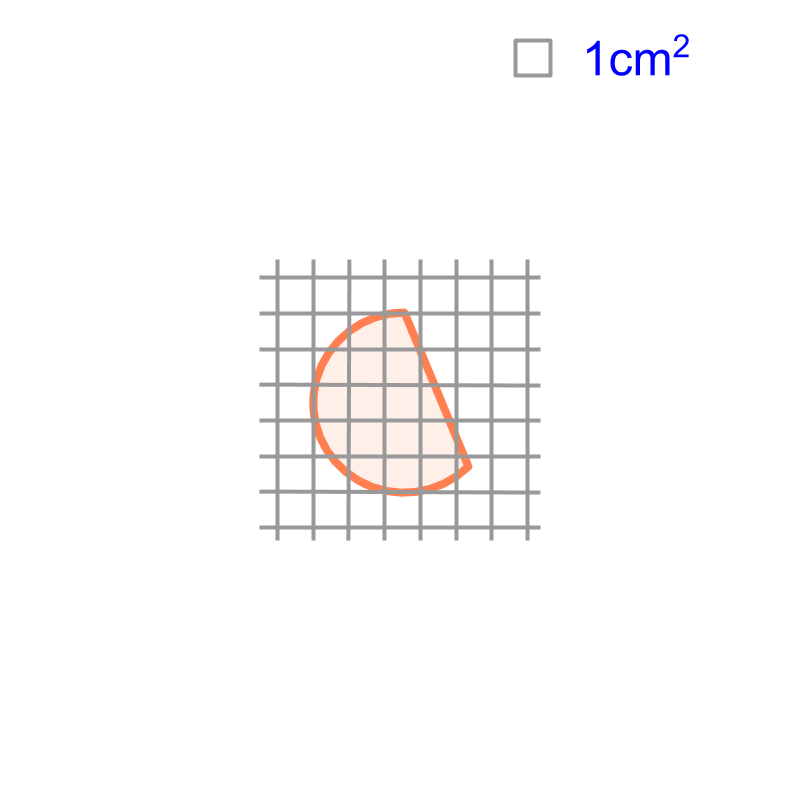
Consider the shape given in the figure. The measurements are not provided. The reference unit-square is shown on the top-right corner. Can we calculate the area of the given shape? Yes, "approximate area can be calculated by superimposing a grid of unit-squares".

The area is approximately $15 c m^{2}$ $15cm^2$ .
area of a shape .
The area is approximated to the count of large squares within the figure.

suitable for some shapes

Measurement by superimposition provides accurate results for

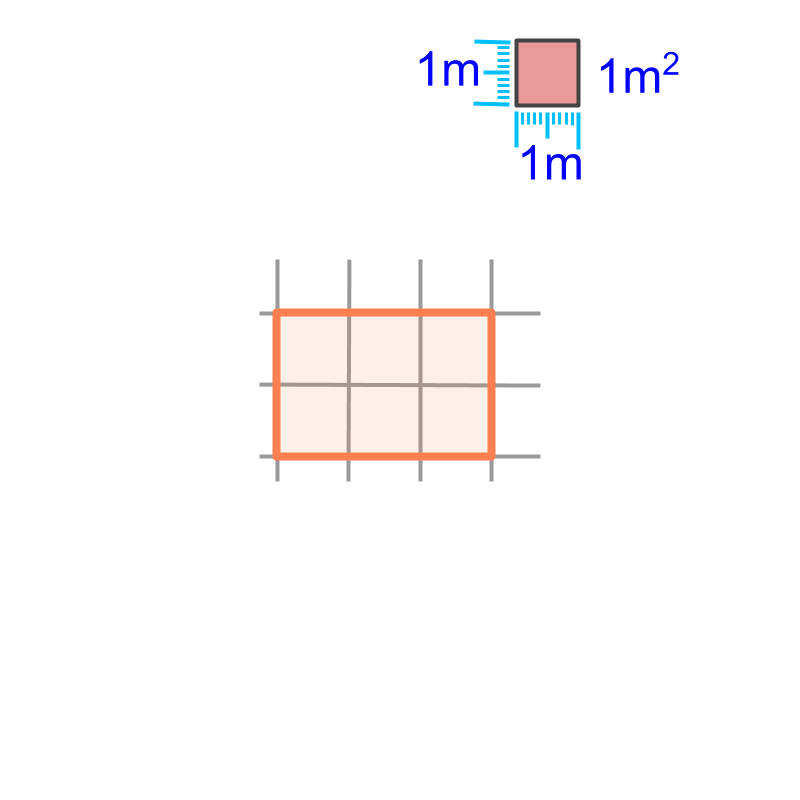
• area of squares and rectangles : The unit-square has $90^{\circ}$ $90^@$ angles at the vertices. And so, the unit-square fits within Squares and Rectangles.
area

• volume of cubes and cuboids : The unit-cube has $90^{\circ}$ $90^@$ angles at the vertices. And so, the unit-cube fits within cubes and cuboids.
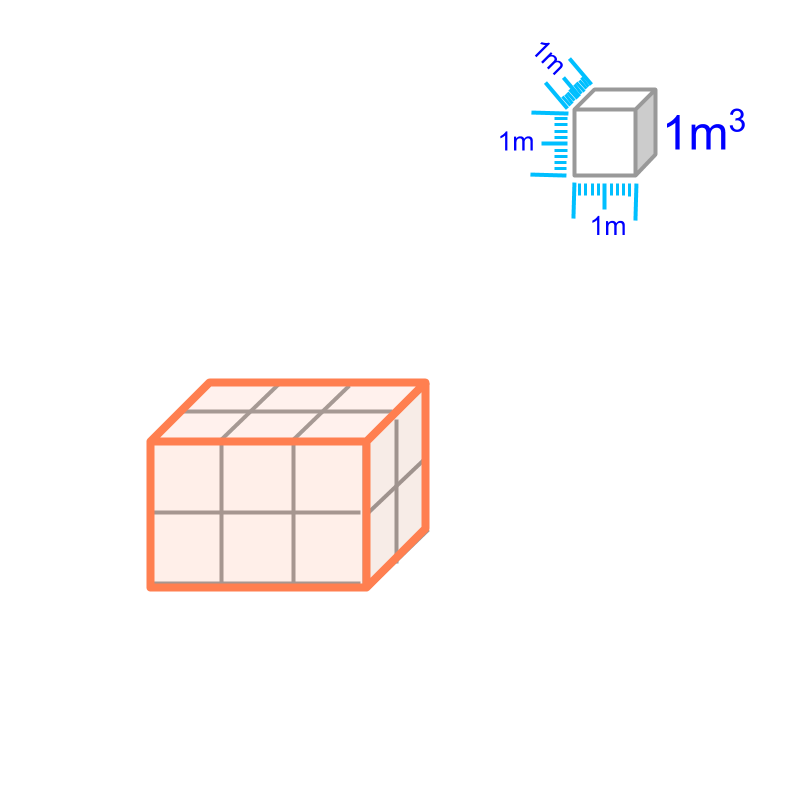
volume
For shapes like triangles or prisms, measurement requires some geometrical calculation or the measurement will be approximate.
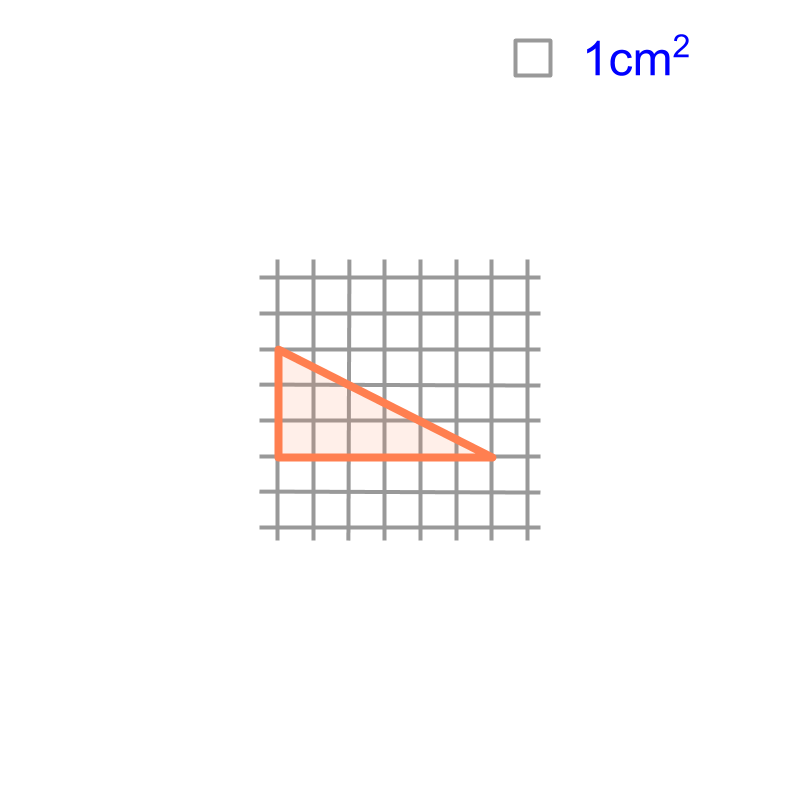
area approximation

summary

Measurement by Superimposition : Length, Area, or Volume can be measured by superimposition of corresponding unit-measures. area by superimposition This method suits best for

• area of squares and rectangles

• volume of cubes and cuboids

Outline

The outline of material to learn Mensuration : Length, Area, and Volume is as follows.

Note 1: click here for the detailed overview of Mensuration High

Note 2: click here for basics of mensuration, which is essential to understand this.

• Basics of measurement

→ Summary of Measurement Basics

→ Measurement by superimposition

→ Measurement by calculation

→ Measurement by equivalence

→ Measurement by infinitesimal pieces

→ Cavalieri's Principle (2D)

→ Cavalieri's Principle (3D)

• Perimeter & Area of 2D shapes

→ Circumference of Circles

→ Area of Circles

• Surface area & Volume of 3D shapes

→ Prisms : Surface Area & Volume

→ Pyramids : Surface Area & Volume

→ Cone : Surface Area & Volume

→ Sphere : Surface Area & Volume

• Part Shapes

→ Understanding part Shapes

→ Circle : Sector and Segment

→ Frustum of a Cone