Mensuration : Length, Area, and Volume : Cone: Surface Area and Volume

maths > mensuration-high

Cone: Surface Area and Volume

what you'll learn...

Overview

Surface Area and Volume of cone: Total surface area of a cone
$=$ $=$ area of the base-surface $+$ $+$ sum of the area of the side-faces

$= 2 π r (r + l)$ $= 2pi r(r+l)$ Volume of a cone
$= \frac{1}{3} \times area of the base-face \times height$ $= 1/3 xx text( area of the base-face ) xx text( height)$

$= \frac{1}{3} π r^{2} h$ $= 1/3 pi r^2 h$

cone

The solid shape shown in the figure is "a cone". Cone is a 3D solid shape with a circular-base at the bottom with a curved surface converging to a single point on the top.

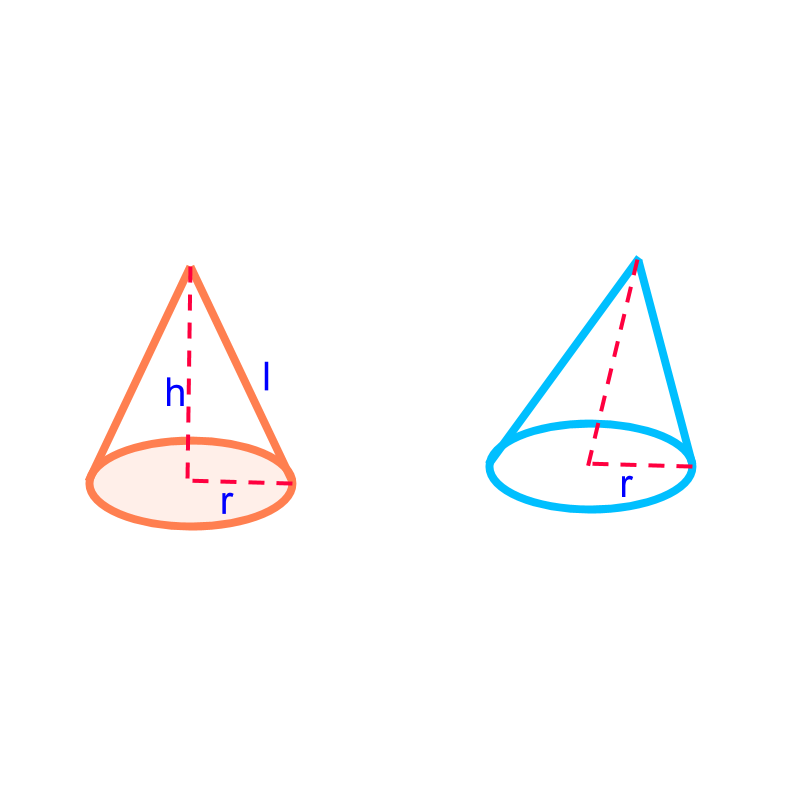
We consider only right-circular-cones with its axis at right angle to the base-surface. Other cones are

(1) elliptical-cones with an ellipse at the base-surface

(2) oblique-cones with the angle, between its axis and the base, not a right-angle.

A right-circular-cone is shown in orange. An oblique-cone is shown in blue.

surface area

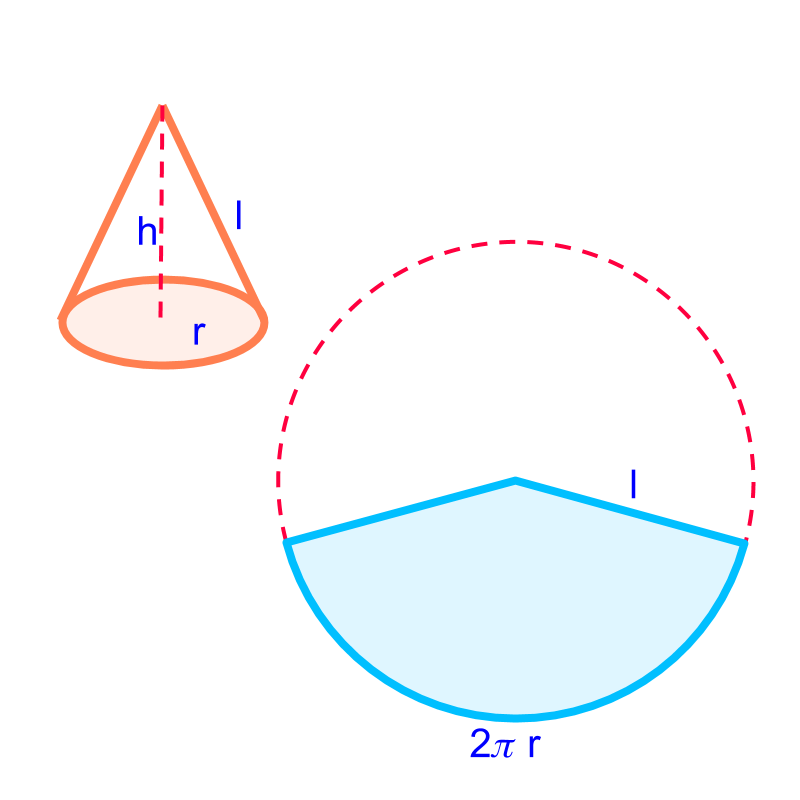
The surface area of the cone of radius $r$ $r$ and height $h$ $h$ is

$area of base$ $text( area of base )$ $+ area of sector$ $+ text( area of sector)$

$area of base$ $text( area of base )$ $+ π radius \times (s l a n t h e i g h t)$ $+ pi text(radius) xx ( slant height)$

$π r (r + s)$ $pi r(r+s)$

Note: A cone consists of

circular base

a sector from a circle with radius of slant-height $s$ $s$ and arc length $2 π r$ $2pi r$ .

$s$ $s$ is the slant height computed as $\sqrt{r^{2} / 4 + h^{2}}$ $sqrt(r^2//4 + h^2)$ .

A cone of height $h$ $h$ is shown in orange. The curved lateral surface is unraveled to a sector as shown in blue. The radius of the sector is the slant-height of the cone $s$ $s$ . And the arc-length of the sector is the perimeter of the base circle of the cone.

Total surface area of the cone

$=$ $=$ area of the base-surface $+$ $+$ the area of the curved surface

$= π r^{2} + a r e a o f a r c$ $= pi r^2 + area of arc$

$= π r^{2} + \frac{2 π r}{2 π s} \times π s^{2}$ $= pi r^2 + (2pi r)/(2pi s) xx pi s^2$

$= π r^{2} + π r s$ $= pi r^2 + pi r s$

`= pi r (r + s)

volume

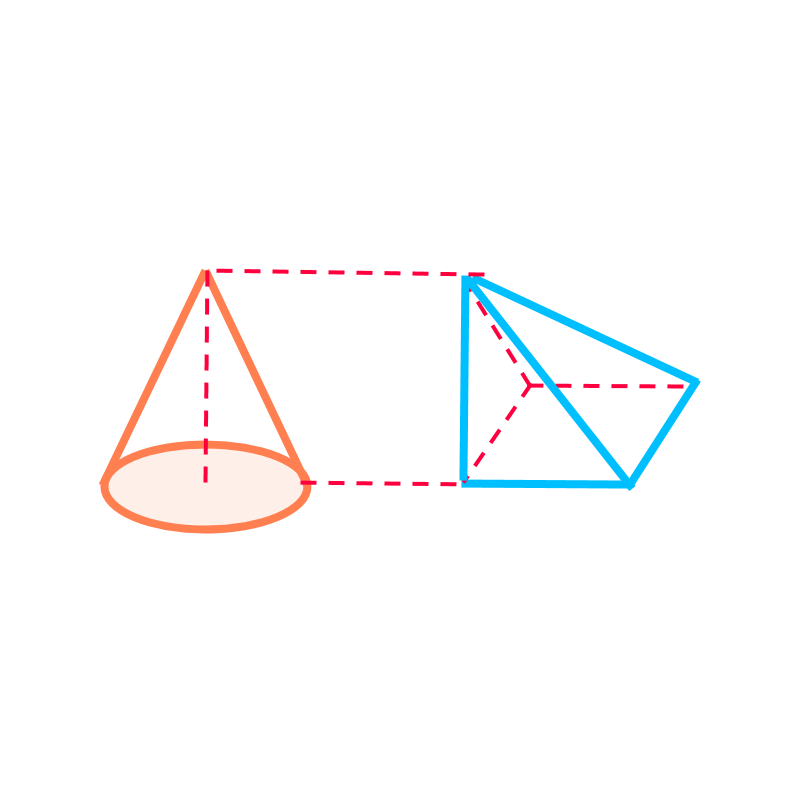
The volume of the cone of radius $r$ $r$ and height $h$ $h$ is

volume of the modified-square-pyramid

$\frac{1}{3} \times area of base-surface$ $1/3 xx text( area of base-surface )$ $\times height$ $xx text( height)$

$\frac{1}{3} π r^{2} h$ $1/3 pi r^2 h$

The cone is shown in orange. As per the Cavalieri's principle in 3D, the cone is equivalently represented by the oblique-pyramid shown in blue.

The modified-pyramid has

• the area at the base surface equal to the area of base-surface of the cone

• the height equal to the height of the cone.

• the cross-sectional area along the vertical axis equal to that of the cone

Volume of the cone

$=$ $=$ volume of the pyramid with identical cross-sectional area along the vertical axis

$= \frac{1}{3} \times area of the base \times height$ $= 1/3 xx text( area of the base ) xx text( height)$

$= \frac{1}{3} \times π r^{2} \times h$ $= 1/3 xx pi r^2 xx h$

$= \frac{1}{3} π r^{2} h$ $= 1/3 pi r^2 h$

What is the volume of a cone of height $7$ $7$ cm and radius $3$ $3$ cm?
The answer is " $66 c m^{3}$ $66cm^3$ "

summary

Outline

The outline of material to learn Mensuration : Length, Area, and Volume is as follows.

Note 1: click here for the detailed overview of Mensuration High

Note 2: click here for basics of mensuration, which is essential to understand this.

• Basics of measurement

→ Summary of Measurement Basics

→ Measurement by superimposition

→ Measurement by calculation

→ Measurement by equivalence

→ Measurement by infinitesimal pieces

→ Cavalieri's Principle (2D)

→ Cavalieri's Principle (3D)

• Perimeter & Area of 2D shapes

→ Circumference of Circles

→ Area of Circles

• Surface area & Volume of 3D shapes

→ Prisms : Surface Area & Volume

→ Pyramids : Surface Area & Volume

→ Cone : Surface Area & Volume

→ Sphere : Surface Area & Volume

• Part Shapes

→ Understanding part Shapes

→ Circle : Sector and Segment

→ Frustum of a Cone