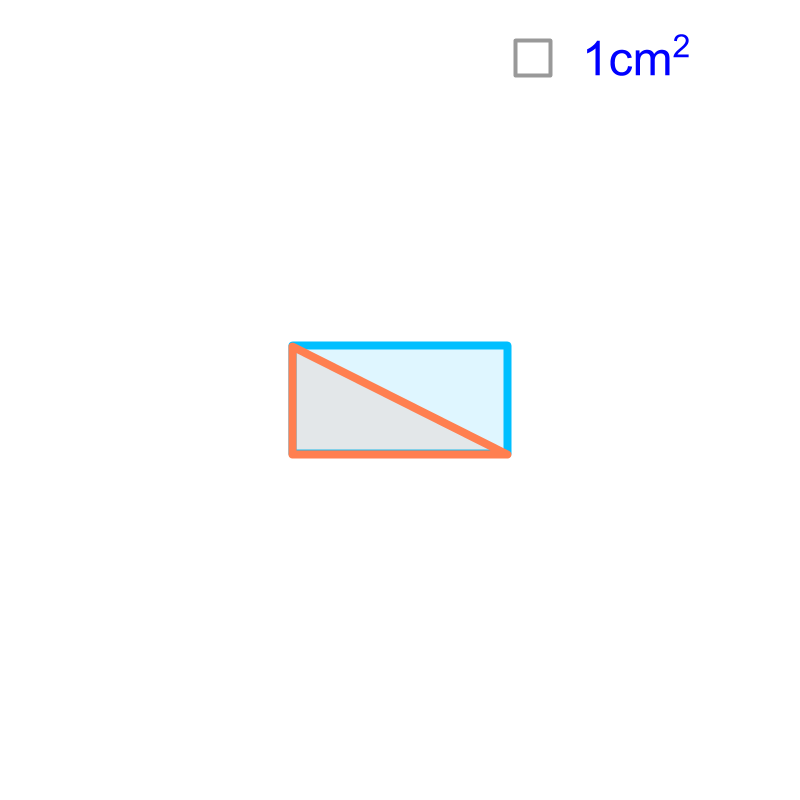
illustrating a problem

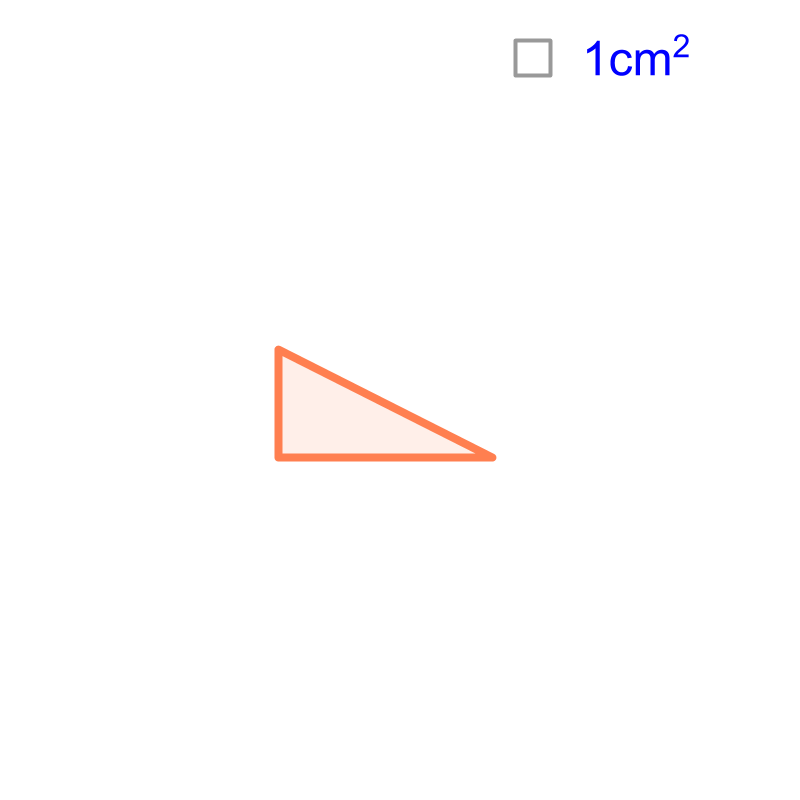
Consider the shape given in the figure. It is a right-triangle of base `6` cm and height `3` cm. Let us superimpose a grid of unit-squares and count the area. Accurate area is not possible to find by this method. Since unit-squares will not fit exactly at the vertices, only approximate area can be computed.

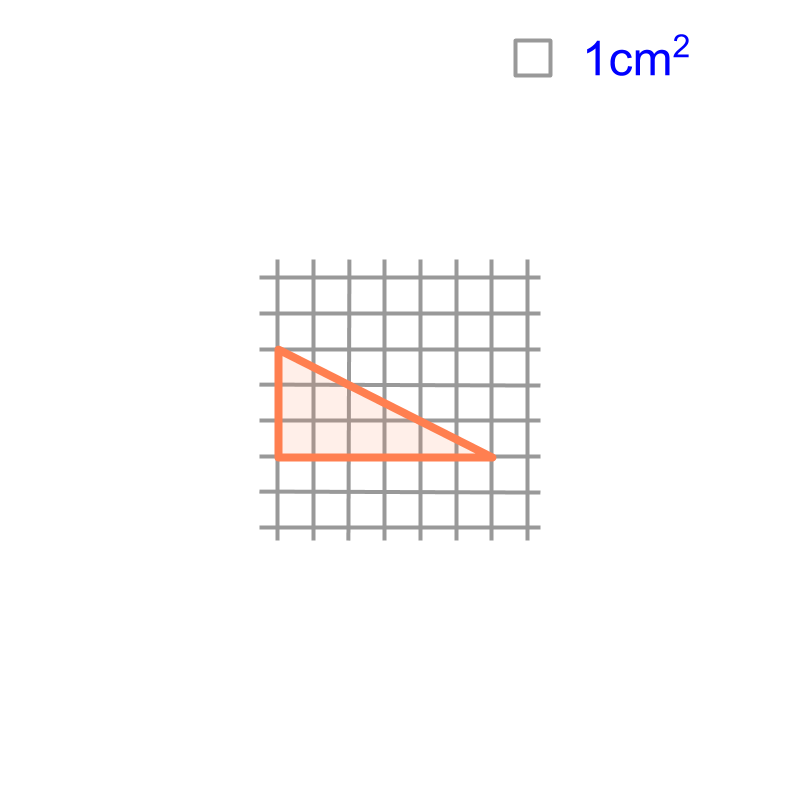
Consider finding area of a right-triangle using grid of unit-squares. The figure illustrates the problem. To find the area, large unit-squares are counted. The approximate area can be either `9cm^2 or`10cm^2`. Though we can further refine the approximation, using unit-squares of millimeter size, it will still have small errors. We are interested in a mathematically rigorous calculation.

calculate

Consider finding area of a right triangle of `6` cm base and `3` cm height. The figure shows the triangle in orange. A rectangle of length `6` cm and width `3` cm is visualized. The rectangle is shown in blue. Geometrically, the hypotenuse of the right triangle splits the rectangle into equal halves. One half is the given right triangle.

We know that the area of the rectangle is length multiplied width. And the right-triangle occupies exact half of the rectangle. It implies that "the area of the triangle is half of the area of the rectangle".

It is geometrically understood that the area of a right-triangle is half of that of the rectangle. And so, the formula for the area is derived as `1/2 text( base ) xx text( height )`.
Note: The proof is given for right-triangles. The same formula is applicable for triangles in general. The proof for all triangles will be given later in the course.

Outline

The outline of material to learn Mensuration : Length, Area, and Volume is as follows.

Note 1: click here for the detailed overview of Mensuration High

Note 2: click here for basics of mensuration, which is essential to understand this.

•  Basics of measurement

  →   Summary of Measurement Basics

  →   Measurement by superimposition

  →   Measurement by calculation

  →   Measurement by equivalence

  →   Measurement by infinitesimal pieces

  →   Cavalieri's Principle (2D)

  →   Cavalieri's Principle (3D)

•  Perimeter & Area of 2D shapes

  →   Circumference of Circles

  →   Area of Circles

•  Surface area & Volume of 3D shapes

  →   Prisms : Surface Area & Volume

  →   Pyramids : Surface Area & Volume

  →   Cone : Surface Area & Volume

  →   Sphere : Surface Area & Volume

•  Part Shapes

  →   Understanding part Shapes

  →   Circle : Sector and Segment

  →   Frustum of a Cone
next