Mensuration : Length, Area, and Volume : Area of a Triangle

maths > mensuration-basics

Area of a Triangle

what you'll learn...

Overview

Area of a Triangle:
$\frac{1}{2} \times base \times (h e i g h t)$ $1/2 xx text( base ) xx ( height)$

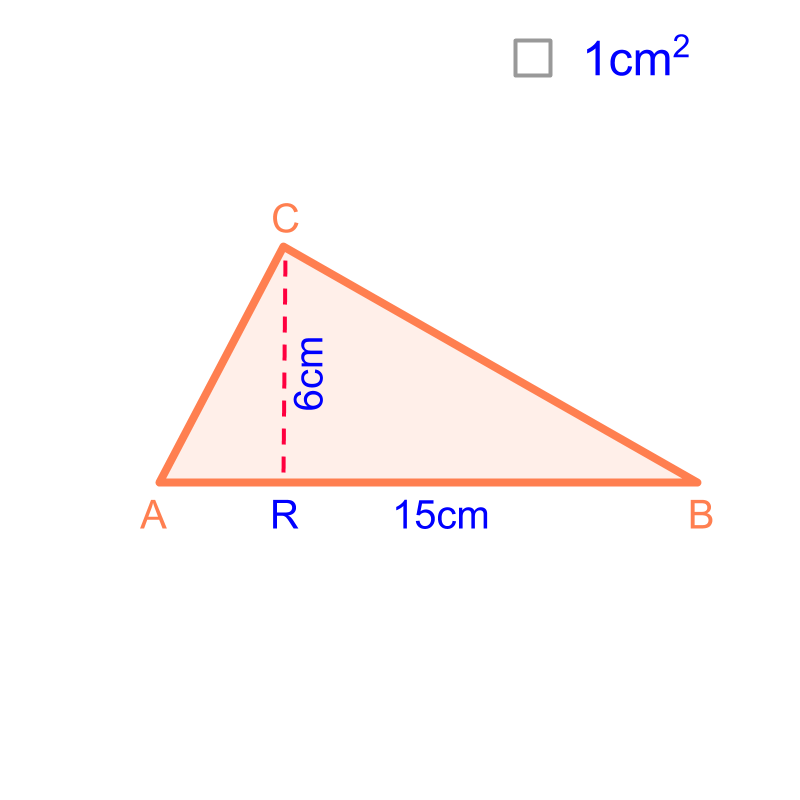
type 1

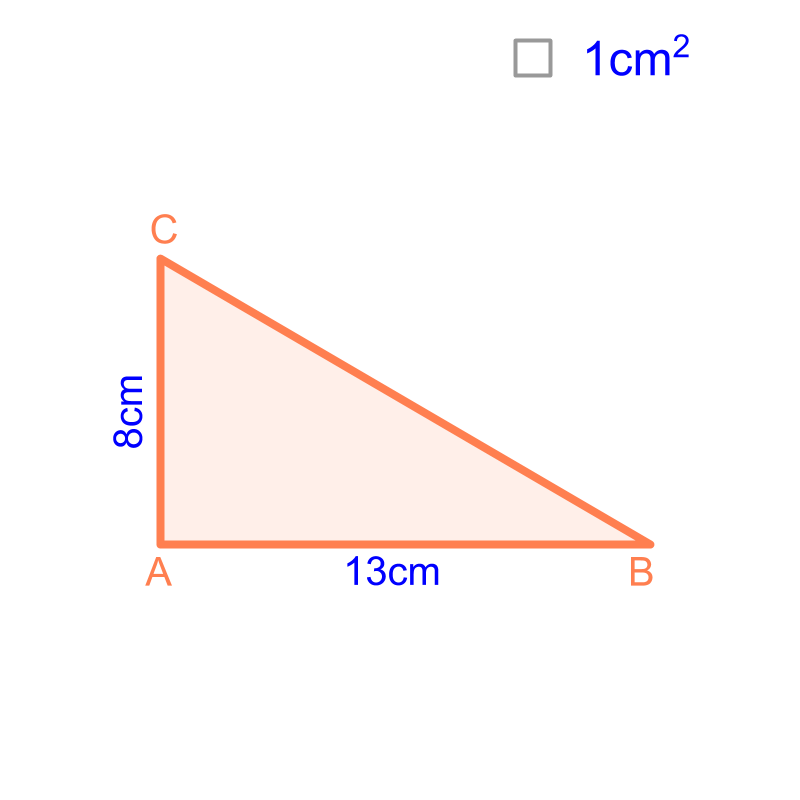
Consider the triangle given in the figure. The base is $13$ $13$ cm and height is $8$ $8$ cm. To find the area of the triangle, compare the triangle with a rectangle of $13$ $13$ cm by $8$ $8$ cm.

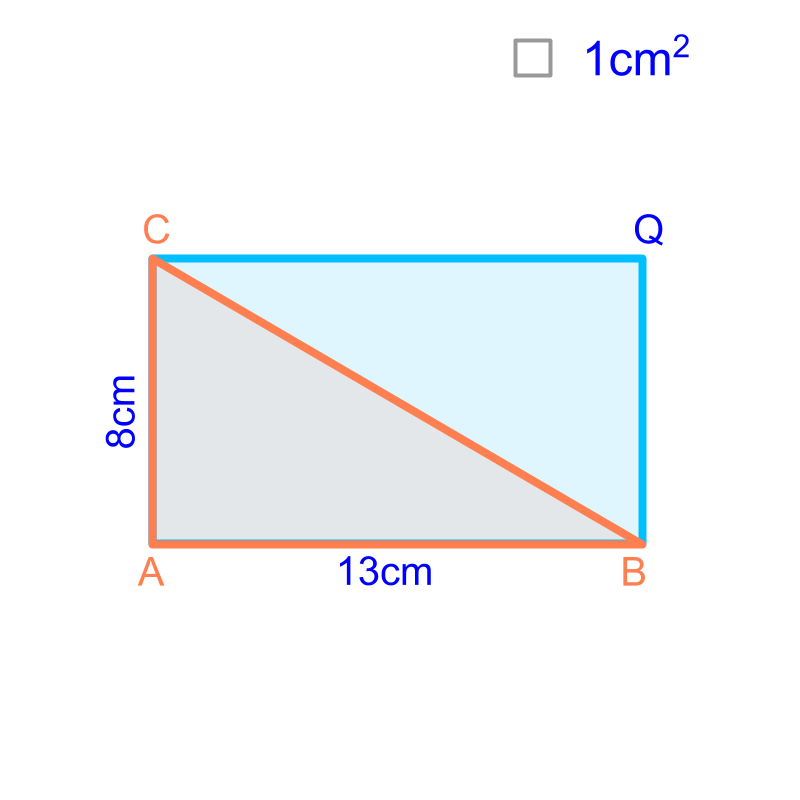
The triangle of base $13$ $13$ cm and height $8$ $8$ cm is placed over a rectangle of length $13$ $13$ cm and width $8$ $8$ cm. It is noted that the triangle splits the rectangle into equal halves. The area of the triangle is half of the area of rectangle OR in other words, $\frac{1}{2} \times base \times (h e i g h t)$ $1/2 xx text( base ) xx ( height)$

type 2

Consider the triangle given in the figure. The base is $15$ $15$ cm and height is $6$ $6$ cm. To calculate the area, compare the triangle with a rectangle of $15$ $15$ cm by $6$ $6$ cm.

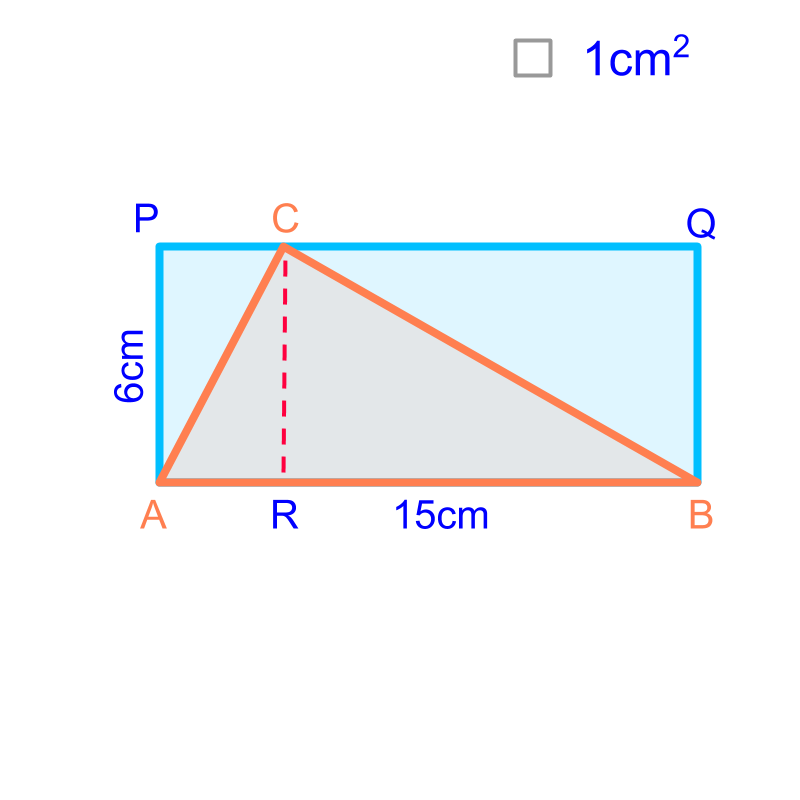
The triangle of base $15$ $15$ cm and height $6$ $6$ cm is placed over a rectangle of length $15$ $15$ cm and width $6$ $6$ cm.

The rectangle is visualized into two parts $A R C P$ $ARCP$ and $R B Q C$ $RBQC$

The triangle is visualized into two parts $△ A R C$ $/_\ARC$ and $△ R B C$ $/_\RBC$

It is noted that the area of the triangle $△ A R C$ $/_\ARC$ is half of the rectangle $A R C P$ $ARCP$ and area of the triangle $△ R B C$ $/_\RBC$ is half of the rectangle $R B Q C$ $RBQC$ .

The area of the triangle $△ A B C$ $/_\ABC$ is sum of area of the two triangles $△ A R C$ $/_\ARC$ and $△ C R B$ $/_\CRB$ .

$=$ $=$ half the area of rectangles $A R C P$ $ARCP$ and $C R B Q$ $CRBQ$ .

$= \frac{1}{2} \times \bar{A R} \times \bar{R C} + \frac{1}{2} \times \bar{R B} \times \bar{R C}$ $= 1/2 xx bar(AR) xx bar(RC) + 1/2 xx bar(RB) xx bar(RC)$

$= \frac{1}{2} \times \bar{R C} \times (\bar{A R} + \bar{R B})$ $= 1/2 xx bar(RC) xx ( bar(AR)+ bar(RB))$

$= \frac{1}{2} \times \bar{R C} \times \bar{A B})$ $= 1/2 xx bar(RC) xx bar(AB))$

$= \frac{1}{2} \times base \times height$ $= 1/2 xx text( base )xx text( height)$

The area of the triangle is half of the area of rectangle OR in other words, $\frac{1}{2} \times base \times (h e i g h t)$ $1/2 xx text( base ) xx ( height)$

type 3

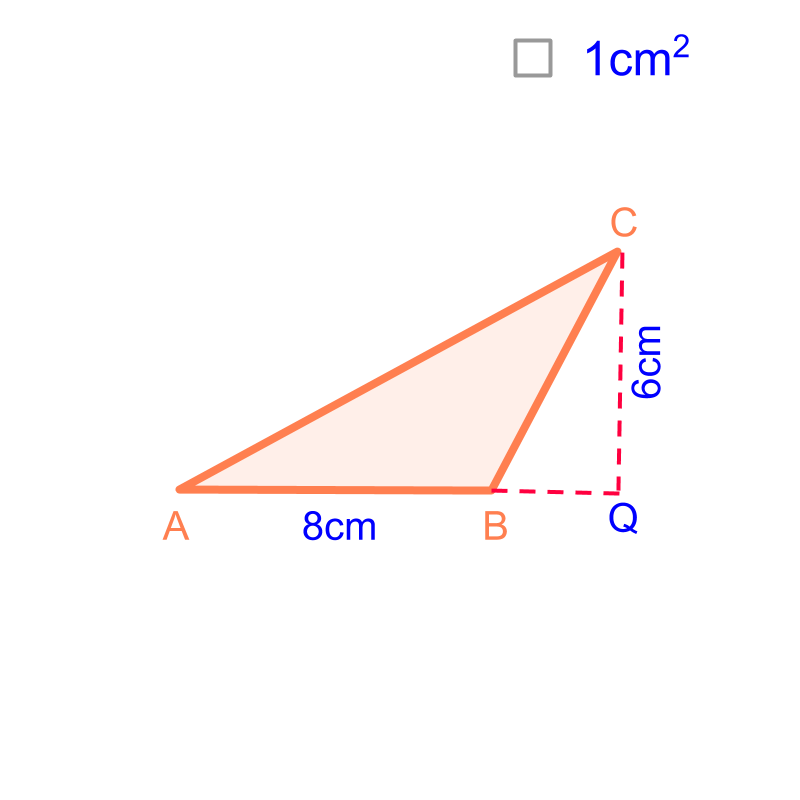
Consider the triangle given in the figure. The base is $8$ $8$ cm and height is $6$ $6$ cm. To calculate the area, compare the triangle with a rectangle covering $A Q C$ $AQC$

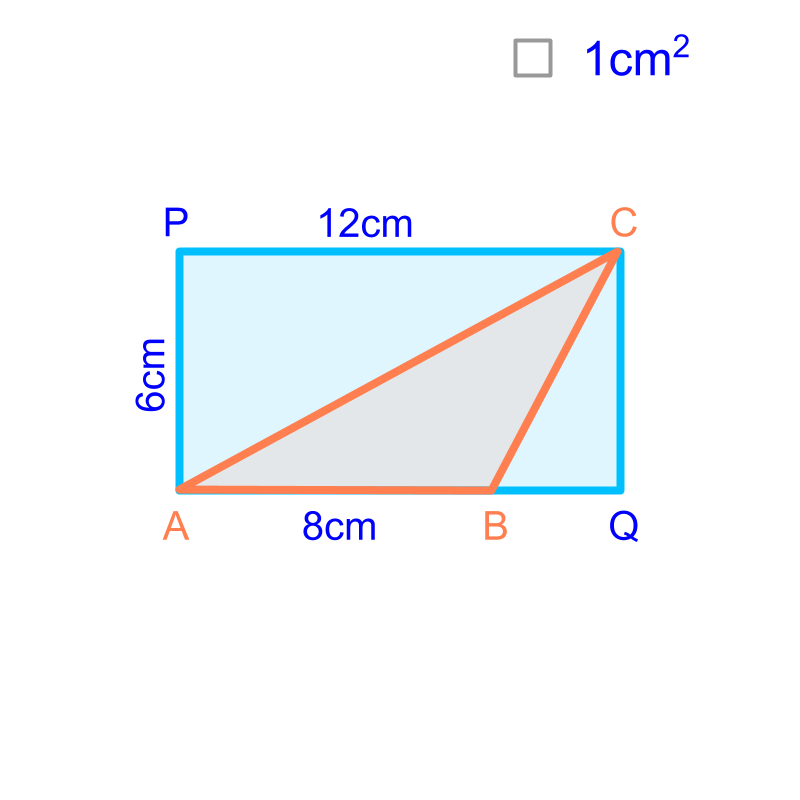
The triangle of base $8$ $8$ cm and height $6$ $6$ cm is placed over a rectangle $A Q C P$ $AQCP$ . The rectangle is visualized to two triangles $△ A Q C$ $/_\AQC$ and $∠ A P C$ $/_APC$ . The area of triangle $△ A Q C$ $/_\AQC$ is half of the rectangle.

The area of the triangle $△ A B C$ $/_\ABC$ is

$=$ $=$ area of $△ A Q C -$ $/_\AQC -$ area of $△ B Q C$ $/_\BQC$

$= \frac{1}{2} \times \bar{A Q} \times \bar{Q C} -$ $= 1/2 xx bar(AQ) xx bar(QC) -$ $\frac{1}{2} \times \bar{B Q} \times \bar{Q C}$ $1/2 xx bar(BQ) xx bar(QC)$

$= \frac{1}{2} \times \bar{Q C} \times (\bar{A Q} - \bar{B Q})$ $= 1/2 xx bar(QC) xx ( bar(AQ) -bar(BQ) )$

$= \frac{1}{2} \times \bar{Q C} \times \bar{A B}$ $= 1/2 xx bar(QC) xx bar(AB)$

$= \frac{1}{2} \times base \times height$ $= 1/2 xx text( base )xx text( height)$

The area of the triangle is half of the area of rectangle OR in other words, $\frac{1}{2} \times base \times (h e i g h t)$ $1/2 xx text( base ) xx ( height)$

common formula

Consider the three types of triangles,
area of a triangle

For all the types, the area is derived as

$\frac{1}{2} \times base \times (h e i g h t)$ $1/2 xx text( base ) xx ( height)$

What is the area of the triangle with base $2$ $2$ cm and height $3$ $3$ cm?
The answer is " $\frac{1}{2} \times 2 \times 3 = 3 c m^{2}$ $1/2 xx 2xx3 = 3cm^2$ "

summary

Area of a Triangle:
$\frac{1}{2} \times base \times (h e i g h t)$ $1/2 xx text( base ) xx ( height)$

Outline

The outline of material to learn "Mensuration basics : Length, Area, & Volume" is as follows.

Note: click here for detailed outline of Mensuration (Basics).

• Measuring Basics

→ Introduction to Standards

→ Measuring Length

→ Accurate & Approximate Meaures

→ Measuring Area

→ Measuring Volume

→ Conversion between Units of Measure

• 2D shapes

→ Perimeter of Polygons

→ Area of Square & rectangle

→ Area of Triangle

→ Area of Polygons

→ Perimeter and area of a Circle

→ Perimeter & Area of Quadrilaterals

• 3D shapes

→ Surface Area of Cube, Cuboid, Cylinder

→ Volume of Cube, Cuboid, Cylinder