Mensuration : Length, Area, and Volume : Perimeter and Area of Various Quadrilaterals

maths > mensuration-basics

Perimeter and Area of Various Quadrilaterals

what you'll learn...

Overview

Area of Some Quadrilaterals : Consider the polygon shapes as combination of triangles and find sum of area of the triangles.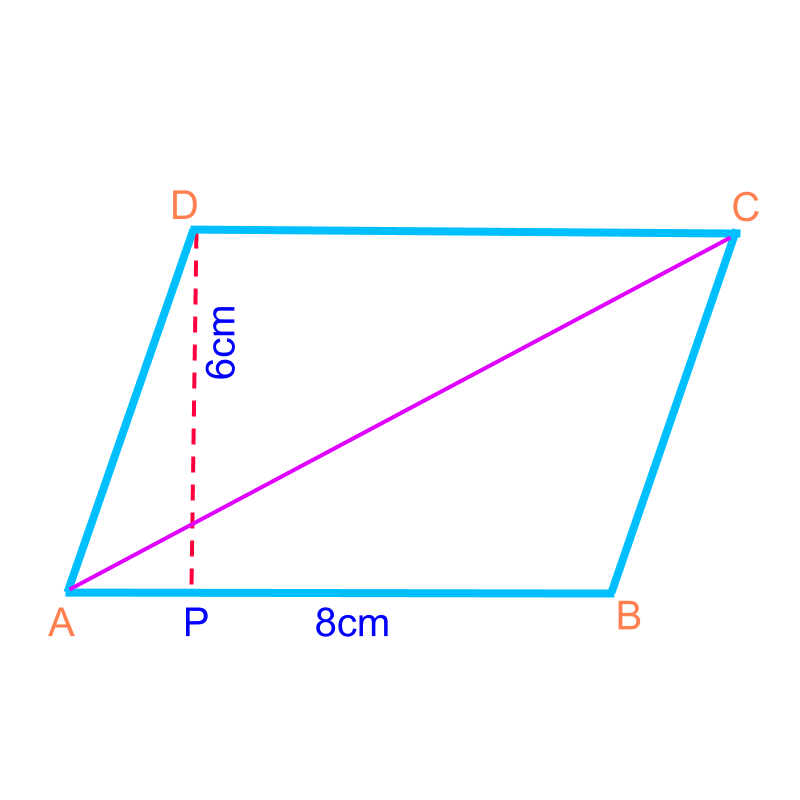 area of parallelogram $area of a parallelogram$ $text( area of a parallelogram )$ $= base \times height$ $= text( base ) xx text( height)$ area of trapezium $area of a trapezium$ $text( area of a trapezium )$ $= \frac{1}{2} \times sum of bases \times height$ $= 1/2 xx text( sum of bases ) xx text( height)$ area of kite $area of a kite$ $text( area of a kite )$ $= \frac{1}{2} \times product of the diagonals$ $= 1/2 xx text( product of the diagonals)$

parallelogram

A parallelogram is a quadrilateral with two pairs of parallel sides.

Consider the parallelogram with base $8$ $8$ cm and height $6$ $6$ cm. The parallelogram is shown in the figure.

In general, to find area of polygons, consider them as combination of triangles. The same is applied to the parallelogram.

The parallelogram $A B C D$ $ABCD$ is considered to be two triangles $△ A B C$ $/_\ABC$ and $△ A C D$ $/_\ACD$ .

The area of parallelogram

$=$ $=$ sum of area of the two triangles

$= \frac{1}{2} \times \bar{A B} \times \bar{P D} + \frac{1}{2} \bar{C D} \times \bar{P D}$ $= 1/2 xx bar(AB) xx bar(PD) + 1/2 bar(CD) xx bar(PD)$

in a parallelogram the opposite sides are equal $\bar{A B} = \bar{C D}$ $bar(AB)=bar(CD)$
$= \bar{A B} \times \bar{P D}$ $= bar(AB) xx bar(PD)$

$area = base \times height$ $text( area )= text( base ) xx text( height)$

trapezium

A trapezium is "a quadrilateral with one pair of parallel sides"

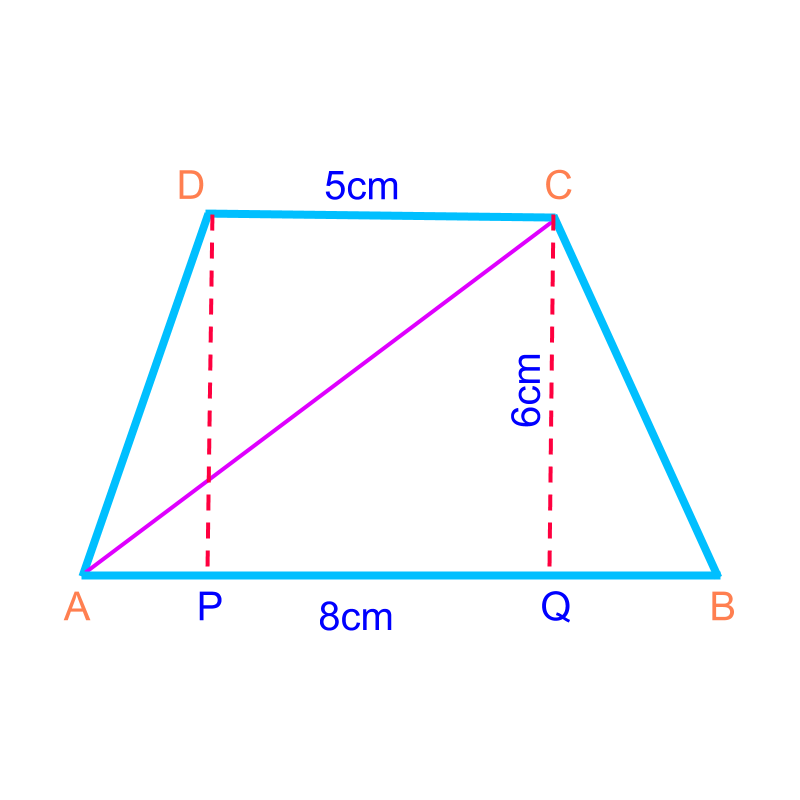
Consider the trapezium with two bases $8$ $8$ cm & $5$ $5$ cm, and height $6$ $6$ cm. The trapezium is shown in the figure.

The trapezium $A B C D$ $ABCD$ is considered as two triangles $△ A B C$ $/_\ABC$ and $△ A C D$ $/_\ACD$ .

The area of trapezium

$=$ $=$ sum of area of the two triangles

$= \frac{1}{2} \times \bar{A B} \times \bar{P D} + \frac{1}{2} \bar{C D} \times \bar{P D}$ $= 1/2 xx bar(AB) xx bar(PD) + 1/2 bar(CD) xx bar(PD)$

$= \frac{1}{2} \times (\bar{A B} + \bar{C D}) \times \bar{P D}$ $= 1/2 xx (bar(AB) + bar(CD)) xx bar(PD)$

$area$ $text( area )$ $= \frac{1}{2} \times sum of bases \times height$ $= 1/2 xx text( sum of bases ) xx text( height)$

kite

A kite is "a quadrilateral with two pair of equal and adjacent sides"

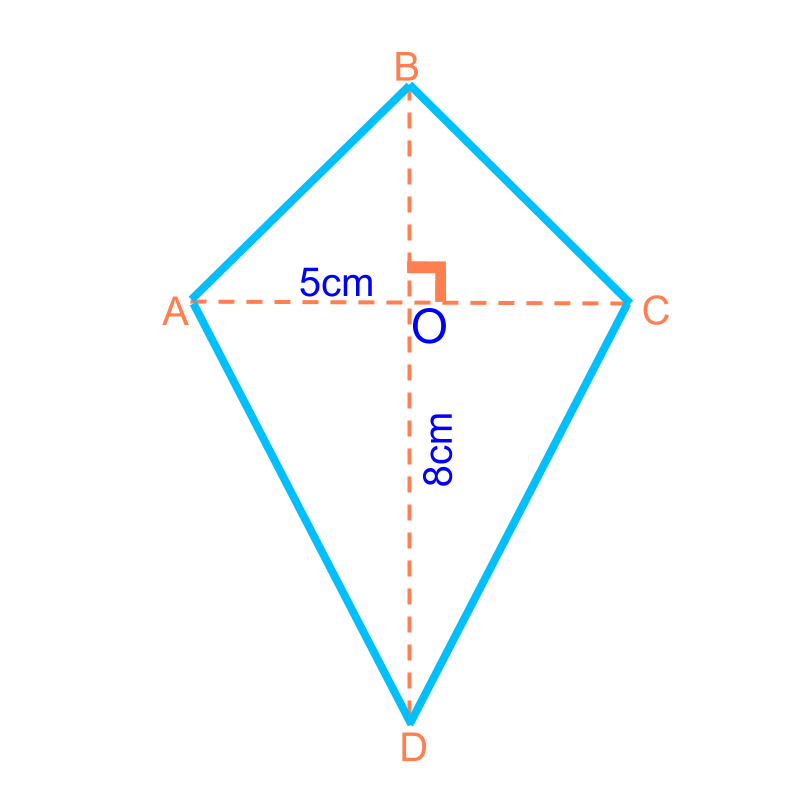
Consider the kite with two diagonals $8$ $8$ cm and height $5$ $5$ cm. The kite is shown in the figure.

The kite $A B C D$ $ABCD$ is considered to be two triangles $△ B D A$ $/_\BDA$ and $△ B D C$ $/_\BDC$ .

The area of kite

$=$ $=$ sum of area of the two triangles

$= \frac{1}{2} \times \bar{B D} \times \bar{A O} + \frac{1}{2} \bar{B D} \times \bar{O C}$ $= 1/2 xx bar(BD) xx bar(AO) + 1/2 bar(BD) xx bar(OC)$

$= \frac{1}{2} \times \bar{B D} \times (\bar{A O} + \bar{O C})$ $= 1/2 xx bar(BD) xx (bar(AO) + bar(OC))$

$= \frac{1}{2} \times \bar{B D} \times \bar{A C}$ $= 1/2 xx bar(BD) xx bar(AC)$

$area = \frac{1}{2} \times product of the diagonals$ $text( area )= 1/2 xx text( product of the diagonals)$

What is the area of a parallelogram of $2$ $2$ cm length and $4$ $4$ cm height?
The answer is " $8 c m^{2}$ $8cm^2$ ".

summary

Outline

The outline of material to learn "Mensuration basics : Length, Area, & Volume" is as follows.

Note: click here for detailed outline of Mensuration (Basics).

• Measuring Basics

→ Introduction to Standards

→ Measuring Length

→ Accurate & Approximate Meaures

→ Measuring Area

→ Measuring Volume

→ Conversion between Units of Measure

• 2D shapes

→ Perimeter of Polygons

→ Area of Square & rectangle

→ Area of Triangle

→ Area of Polygons

→ Perimeter and area of a Circle

→ Perimeter & Area of Quadrilaterals

• 3D shapes

→ Surface Area of Cube, Cuboid, Cylinder

→ Volume of Cube, Cuboid, Cylinder