Mensuration : Length, Area, and Volume : Area of Polygons

maths > mensuration-basics

Area of Polygons

what you'll learn...

Overview

Area of a Polygon : Consider a polygon to be combination of known geometrical forms, mostly triangles.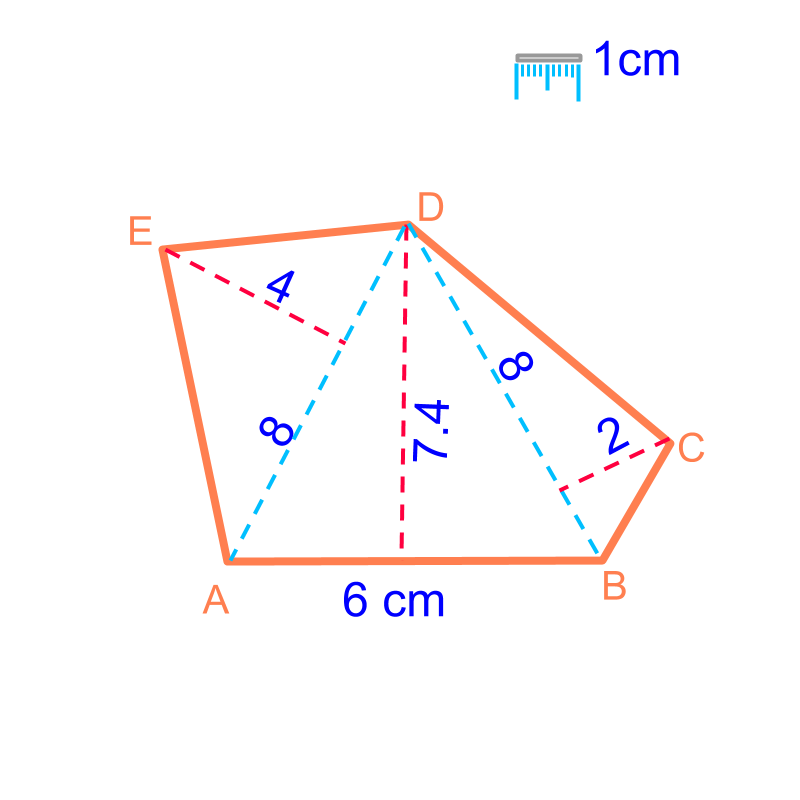 The geometrical forms and the formula for area are:

Area of a triangle $= \frac{1}{2} \times base \times height$ $= 1/2 xx text( base ) xx text( height)$

Area of a trapezium $= \frac{1}{2} \times sum of bases \times height$ $= 1/2 xx text( sum of bases ) xx text( height)$

Area of a parallelogram $= base \times height$ $= text( base ) xx text( height)$

Area of a kite $= \frac{1}{2} \times major-diagonal \times d2$ $= 1/2 xx text( major-diagonal ) xx text( d2)$

all are combination of triangles

Consider the polygon shown in the figure. To find the area of the polygon, "consider the polygon as combination of triangles".

Area of the polygon

$=$ $=$ area of $△ A B D +$ $/_\ABD +$ area of $△ D B C$ $/_\DBC$ + area of $△ A D E$ $/_\ADE$ .

The formula for area of triangle is used to find the area of the polygons.

What is the area of a quadrilateral with all internal angles $90^{\circ}$ $90^@$ and two sides $4$ $4$ cm and $3$ $3$ cm?
This can be solved as
1. two triangles with combined area $2 \times \frac{1}{2} \times 4 \times 3 = 12 c m^{2}$ $2 xx 1/2 xx 4 xx 3 = 12cm^2$
2. area of the rectangle $4 \times 3 = 12 c m^{2}$ $4 xx 3 = 12 cm^2$

summary

Outline

The outline of material to learn "Mensuration basics : Length, Area, & Volume" is as follows.

Note: click here for detailed outline of Mensuration (Basics).

• Measuring Basics

→ Introduction to Standards

→ Measuring Length

→ Accurate & Approximate Meaures

→ Measuring Area

→ Measuring Volume

→ Conversion between Units of Measure

• 2D shapes

→ Perimeter of Polygons

→ Area of Square & rectangle

→ Area of Triangle

→ Area of Polygons

→ Perimeter and area of a Circle

→ Perimeter & Area of Quadrilaterals

• 3D shapes

→ Surface Area of Cube, Cuboid, Cylinder

→ Volume of Cube, Cuboid, Cylinder