Mensuration : Length, Area, and Volume : Prisms : Surface Area and Volume

maths > mensuration-high

Prisms : Surface Area and Volume

what you'll learn...

Overview

Surface Area and Volume of Prism: Total surface area of a prism
$=$ $=$ area of the two faces on the top and bottom $+$ $+$ the area of the vertical faces

$=$ $=$ area of the two faces on the top and bottom $+$ $+$ height multiplied perimeter of the top or bottom face. Volume of a prism
$= area of the top or bottom face \times height$ $= text( area of the top or bottom face ) xx text( height)$

prism

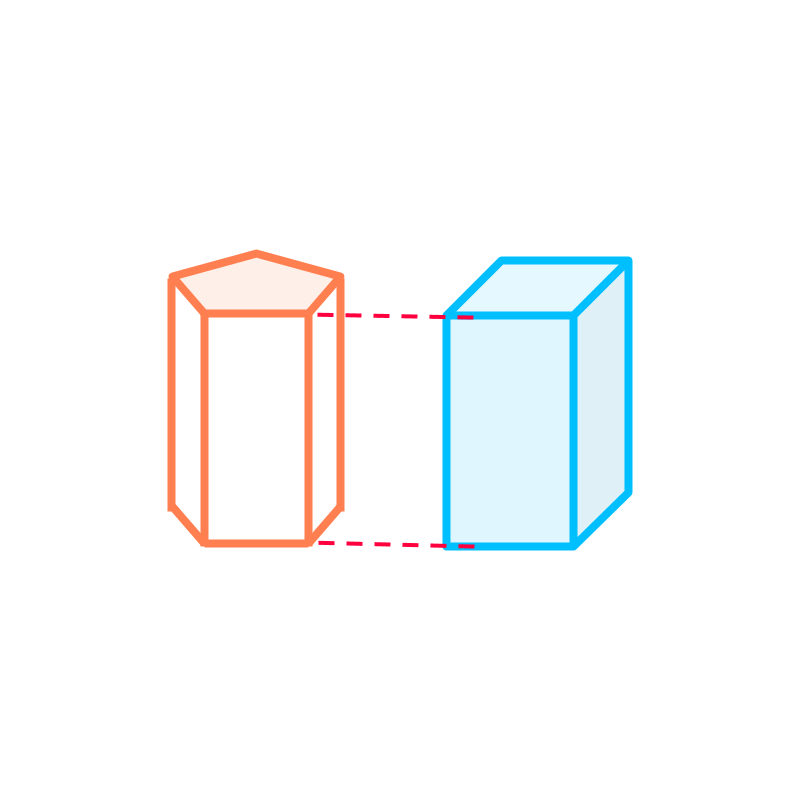
The shape shown in the figure is "a prism".

Prism is a 3D solid shape with a cross section of a 2D-polygon uniformly along its axis. The cross section can be any 2D-polygon, for example, square, rectangle, triangle, etc, and the prisms are square-prism, rectangular-prism, triangular-prism respectively.

We consider only right-prisms with its axis at right angle to the top and bottom faces. The oblique-prisms have the angle between its axis and the top (or bottom) face is not a right-angle. A right-prism is shown in orange. An oblique prism is shown in blue.

surface area

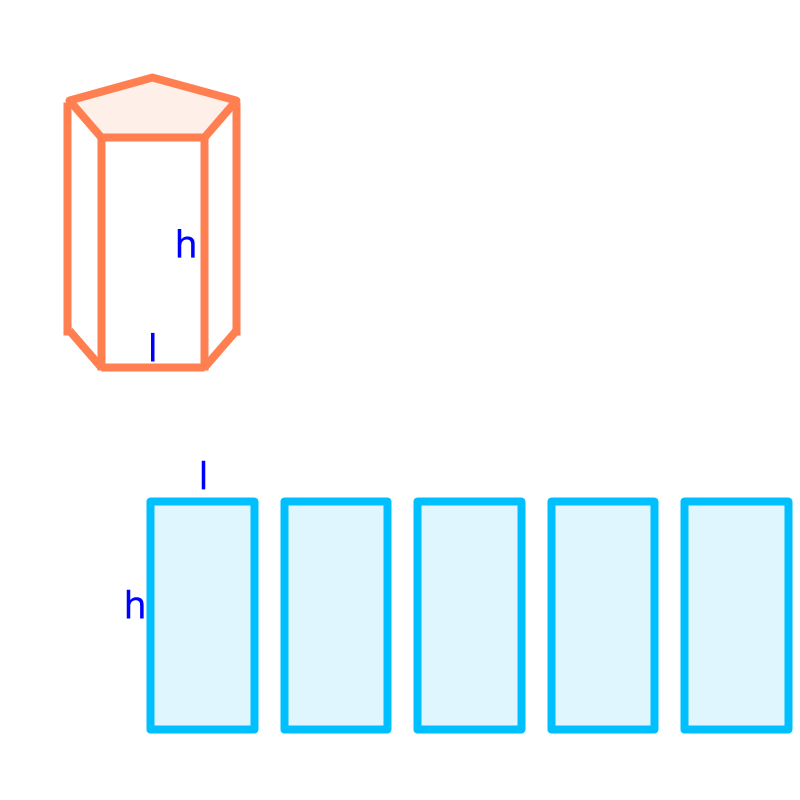
A generic prism consists of top and bottom faces of a 2D-shape, (in this problem a regular-pentagons) a set of vertical rectangular faces, (in this problem $5$ $5$ rectangles of sides $l$ $l$ and $h$ $h$ ). The surface area of the regular-pentagonal-prism of side $l$ $l$ and height $h$ $h$ is $2 \times area of pentagon$ $2 xx text( area of pentagon )$ $+ 5 \times area of rectangles$ $+ 5 xx text( area of rectangles)$ or $2 \times area of pentagon$ $2 xx text( area of pentagon )$ $+ perimeter of pentagon \times (h e i g h t)$ $+ text( perimeter of pentagon) xx ( height)$

A prism of height $h$ $h$ is shown in orange. The vertical surfaces are visualized into number of rectangles as shown in blue. Area of all these rectangles is the height multiplied sum of its sides, which is height multiplied perimeter of the top or bottom face.

Total surface area of the prism

$=$ $=$ area of the two faces on the top and bottom $+$ $+$ the area of the vertical faces

$=$ $=$ area of the two faces on the top and bottom $+$ $+$ height multiplied perimeter of the top or bottom face.

volume

The volume of the regular-pentagonal-prism of side $l$ $l$ and height $h$ $h$ is " $area of pentagon$ $text( area of pentagon )$ $\times height$ $xx text( height)$ ".

A prism of height $h$ $h$ is shown in orange. A cuboid is visualized as shown in blue, such that the cross-sectional area of the prism equals that of the cuboid along the vertical axis. As per Cavalieri's principle, the volumes of these two solids are equal.

Volume of the prism

$=$ $=$ volume of the cuboid with identical cross sectional area and height

$= area of a face \times height$ $= text( area of a face ) xx text( height)$

What is the volume of prism with base area $20 c m^{2}$ $20cm^2$ and height $4$ $4$ cm?

The answer is " $= 80 c m^{3}$ $=80cm^3$ "

summary

Outline

The outline of material to learn Mensuration : Length, Area, and Volume is as follows.

Note 1: click here for the detailed overview of Mensuration High

Note 2: click here for basics of mensuration, which is essential to understand this.

• Basics of measurement

→ Summary of Measurement Basics

→ Measurement by superimposition

→ Measurement by calculation

→ Measurement by equivalence

→ Measurement by infinitesimal pieces

→ Cavalieri's Principle (2D)

→ Cavalieri's Principle (3D)

• Perimeter & Area of 2D shapes

→ Circumference of Circles

→ Area of Circles

• Surface area & Volume of 3D shapes

→ Prisms : Surface Area & Volume

→ Pyramids : Surface Area & Volume

→ Cone : Surface Area & Volume

→ Sphere : Surface Area & Volume

• Part Shapes

→ Understanding part Shapes

→ Circle : Sector and Segment

→ Frustum of a Cone