Mensuration : Length, Area, and Volume

maths

Welcome to the lessons that give firm foundation in measuring perimeter, area, and volume.

To measure a length, area, or volume one of the following methods is used.

• Measurement by Superimposition, Calculation and Equivalence

• Equivalence by infinitesimal pieces, and Cavalieri's Principle

Once the above is understood, the formula for perimeter, area, and volume of 2D and 3D shapes are provided.

Start learning derivations of the formulas of mensuration.

This requires some review and rework. Though all relevant information is documented, it is not sufficiently explained and properly connected. If people read, then I'll put my effort in fixing that.

maths > mensuration-high > measuring-basics-summary

Summary of Measurement Basics

Revising the concepts:

• Absolute Standards are standards defined independent of any other measures.

• Derived Standards are standards derived using one or more of absolute standards.

• Length is the distance-span between two points.

• Area is the surface-span of a closed plane figure.

• Volume is the space-span of a closed solid figure.

maths > mensuration-high > measuring-by-superimposition

Measurement by superimposition

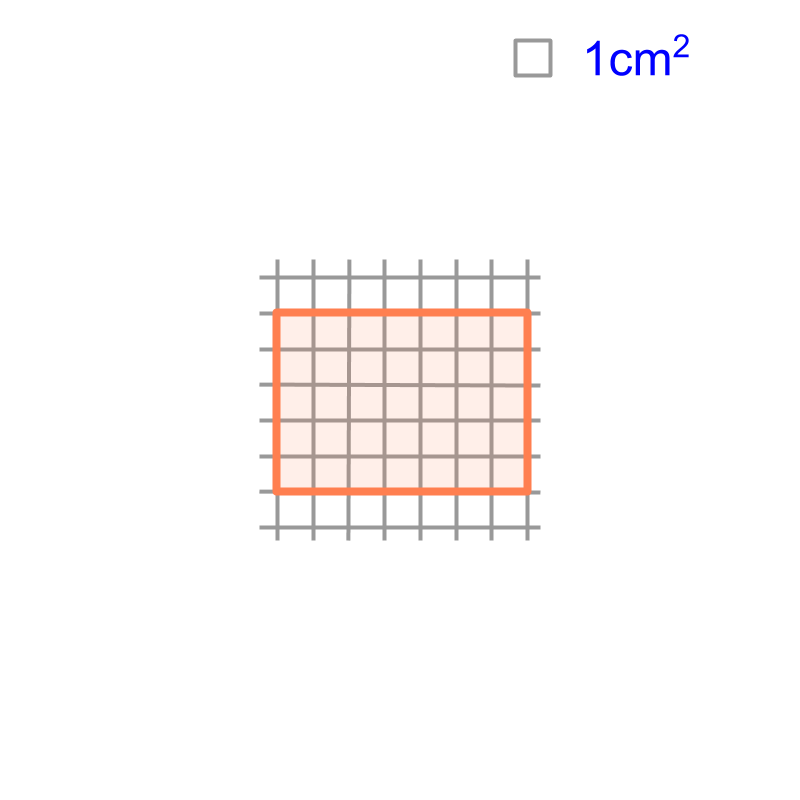
To measure a length, area, or volume one of the three methods is used. THe first method is Measurement by Superimposition. Length, Area, or Volume can be measured by superimposition of corresponding unit-measures. area by superimposition

maths > mensuration-high > measuring-by-calculation

Measurement by Calculation

To measure a length, area, or volume one of the three methods is used. The second method is Measurement by Calculation. Length, Area, or Volume can be measured by calculations involving geometrical principles.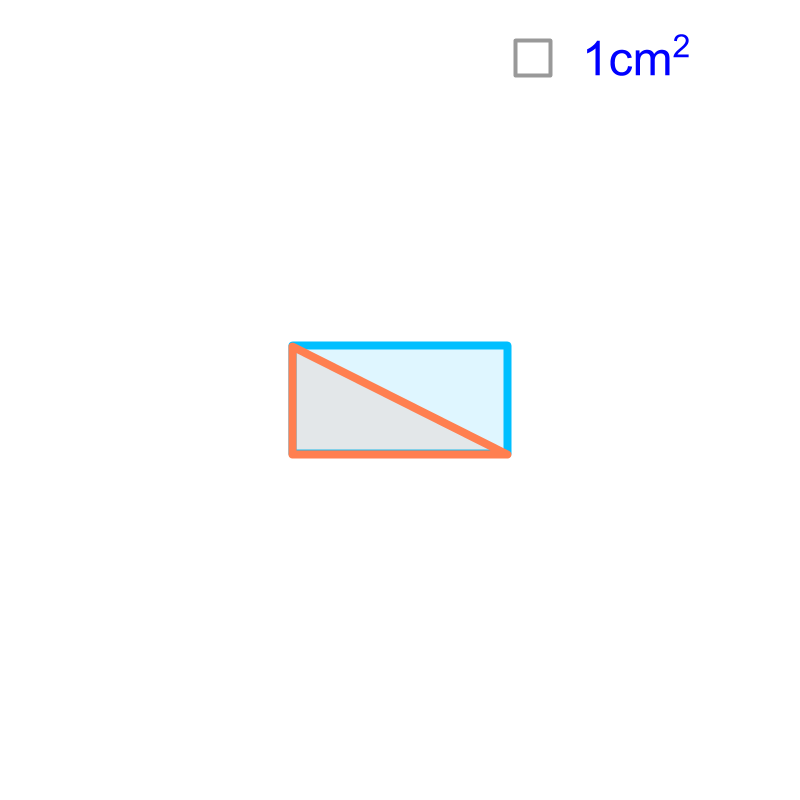 area by calculation

maths > mensuration-high > measuring-by-equivalence

Measurement by Equivalence

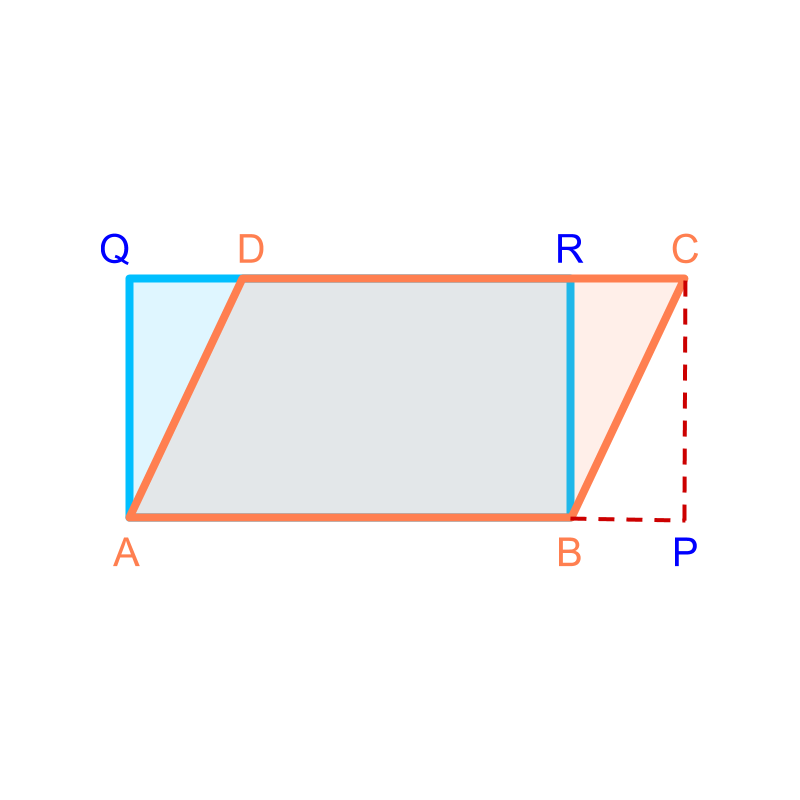
To measure a length, area, or volume one of the three methods is used. The the third method is " Measurement by Equivalence". Measurement by Equivalence: Length, Area, or Volume can be measured by constructing an equivalent shape or object involving geometrical principles. area by equivalence

maths > mensuration-high > measuring-equivalence-by-infinitesimal

Equivalence by Infinitesimal Pieces

Three methods are used to find equivalence when employing measurement by equivalence. The first method is Equivalence by Infinitesimal Pieces. Length, Area, and Volume can be measured by equivalence with infinitesimal pieces. area by equivalence An example of finding perimeter of a circle is illustrated in the figure. The circle is spanned with isosceles triangles.

Approximate value of the perimeter of the circle equals sum of the bases of the triangles.

Accurate value of the perimeter of the circle is calculated by making the triangles infinitesimal small.

maths > mensuration-high > measuring-cavalieri-area

Cavalieri's Principle (2D)

Three methods are used to find equivalence when employing measurement by equivalence. The second method is Cavalieri's Principle in 2D : For a given two shapes on a plane, a line intersecting the shapes is considered. The length of the intersecting line segments $\bar{A B}$ $bar(AB)$ and $\bar{C D}$ $bar(CD)$ are considered. area by cavalieri principle If the length of the intersecting line-segments are equal for all parallel lines to the intersecting line, then the areas of the two shapes are equal.

maths > mensuration-high > measuring-cavalieri-volume

Cavalieri's Principle (3D)

Three methods are used to find equivalence when employing measurement by equivalence. The third method is Cavalieri's Principle in 3D. For a given two solids, a plane intersecting the solids is considered. The area of the intersecting cross-sections $P$ $P$ and $Q$ $Q$ are considered. volume by cavalieri principle If the areas of intersecting cross-sections are equal for all planes parallel to the intersecting plane, then the volumes of the two solids are equal.

maths > mensuration-high > revision-polygons-perimeter-area

Perimeter & Area: Square, Rectangle, Triangle, Polygons

Finding perimeter and area of simple figures (squares, rectangle, triangle, polygon) are revised without much discussion.

maths > mensuration-high > perimeter-circle

Circumference of a Circle

Circumference of a circle of $1$ $1$ cm diameter is computed to be a decimal value that does not end or repeat. It is calculated to be $3.14159 \dots$ $3.14159cdots$ by approximating the circle to infinitesimally small triangular pieces. area by equivalence That accurate value is represented by the symbol $π$ $pi$ and approximate value of that is $\frac{22}{7}$ $22/7$ and $3.14$ $3.14$ .

Circumference of a circle of $d$ $d$ cm diameter is computed to be $d$ $d$ times the circumference of the circle of $1$ $1$ cm diameter.

Thus the generic formula for the circumference of a circle is $π d$ $pi d$ or $2 π r$ $2 pi r$ .

maths > mensuration-high > area-circle

Area of a circle

Circumference of a circle of $1$ $1$ cm diameter is computed to be a decimal value that does not end or repeat. That accurate value is represented by the symbol $π$ $pi$

Area of a circle of $1$ $1$ cm diameter is computed to be a decimal value that does not end or repeat. That accurate value is taken to be another value $α$ $alpha$ . It can be calculated to be a value by approximating the circle to infinitesimally small triangular pieces. area by equivalence We derive / prove that $α = π$ $alpha = pi$

Area of a circle of $r$ $r$ cm radius is computed to be $r$ $r$ times the area of the circle of $1$ $1$ cm diameter.

Thus the generic formula for the area of a circle is $π r^{2}$ $pi r^2$

maths > mensuration-high > surface-area-volume-basic-shapes

Revision : Cube, Cuboid, Cylinder

Finding surface area of simple figures (cube, cuboid, cylinder) are revised without much discussion.

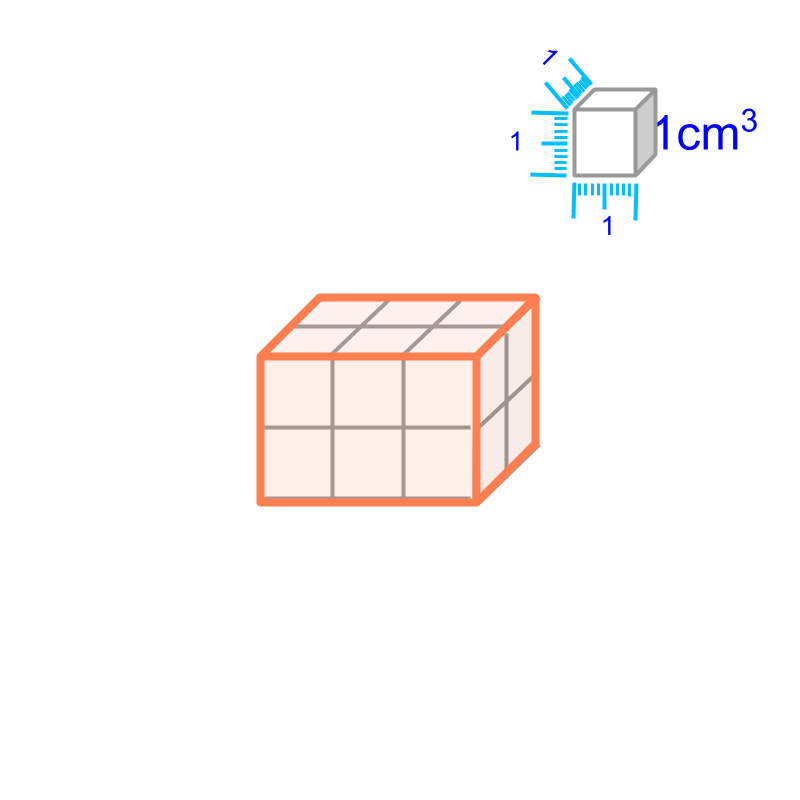cuboid surface area Surface Area of cube $= 6 q^{2}$ $= 6q^2$

Surface Area of cuboid $= 2 (l b + b h + h l)$ $= 2(lb+bh+hl)$

Curved Surface Area of Cylinder $= 2 π r h$ $= 2pi r h$

Surface Area of cylinder $= 2 π r (r + h)$ $=2pi r (r+h)$

maths > mensuration-high > surface-area-volume-prisms

Prisms : Surface Area and Volume

In this page, Finding surface area and volume of prism is explained.

Surface Area and Volume of Prism: 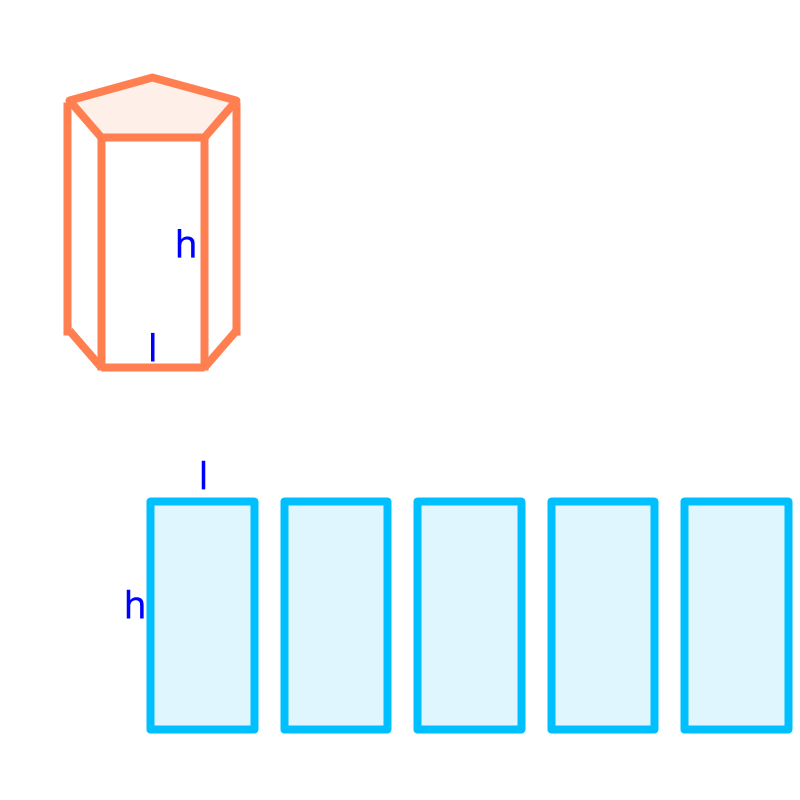Total surface area of a prism
$=$ $=$ area of the two faces on the top and bottom $+$ $+$ the area of the vertical faces

$=$ $=$ area of the two faces on the top and bottom $+$ $+$ height multiplied perimeter of the top or bottom face. 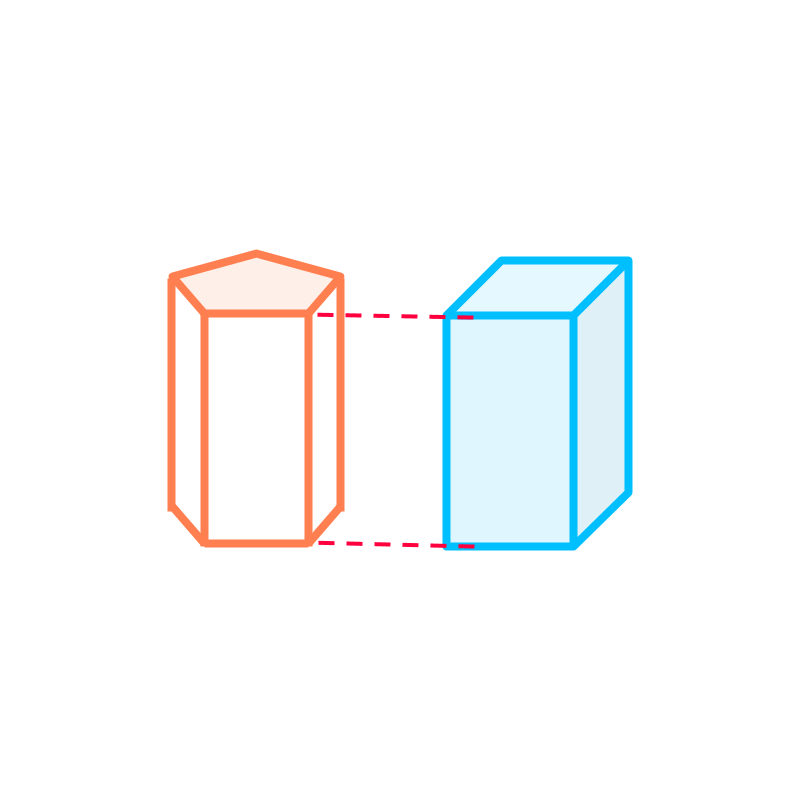Volume of a prism
$= area of the top or bottom face \times height$ $= text( area of the top or bottom face ) xx text( height)$

maths > mensuration-high > surface-area-volume-pyramids

Pyramids : Surface Area and Volume

In this page, finding surface area and volume of pyramids is explained.

Surface Area and Volume of pyramid: surface area of a pyramid Total surface area of the pyramid
$=$ $=$ area of the base-surface $+$ $+$ sum of the area of the side-faces 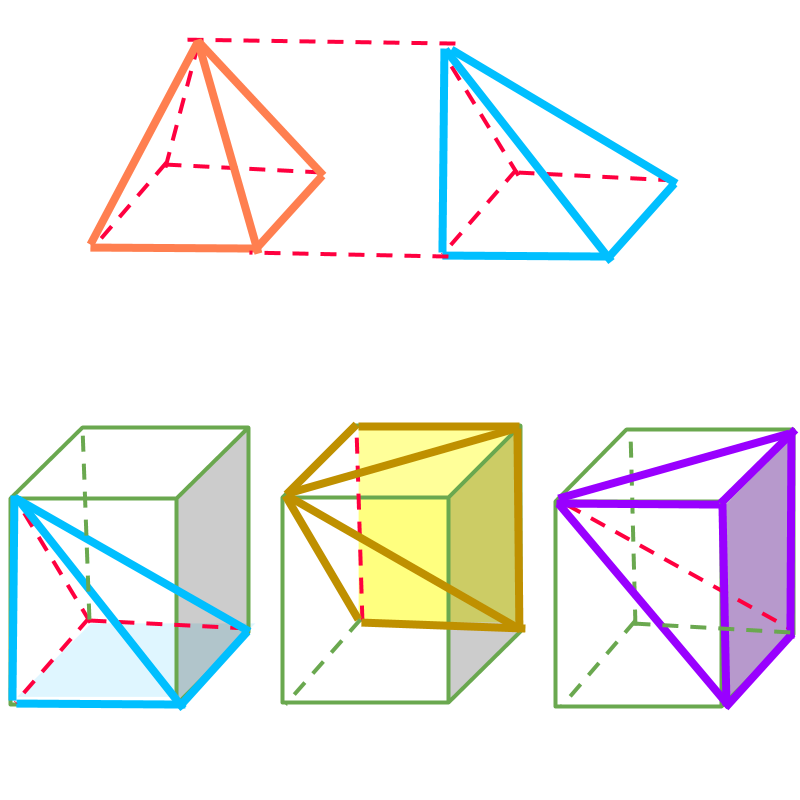volume of a pyramid Volume of the pyramid
$= \frac{1}{3} \times area of the base-face \times height$ $= 1/3 xx text( area of the base-face ) xx text( height)$

maths > mensuration-high > surface-area-volume-cone

Cone: Surface Area and Volume

In this page, Finding surface area and volume of cone is explained.

Surface Area and Volume of cone: 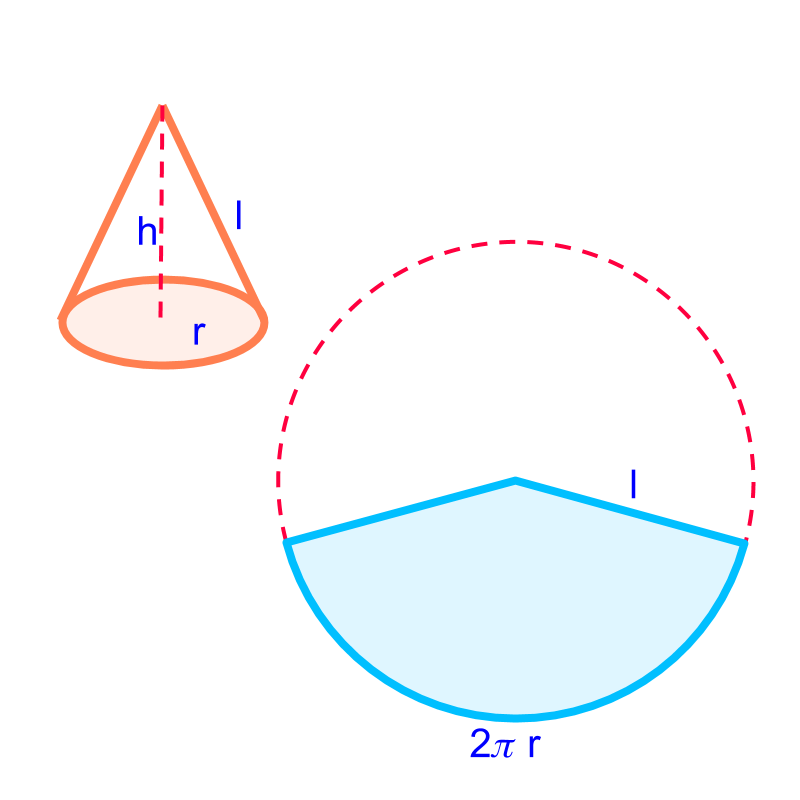Total surface area of a cone
$=$ $=$ area of the base-surface $+$ $+$ sum of the area of the side-faces

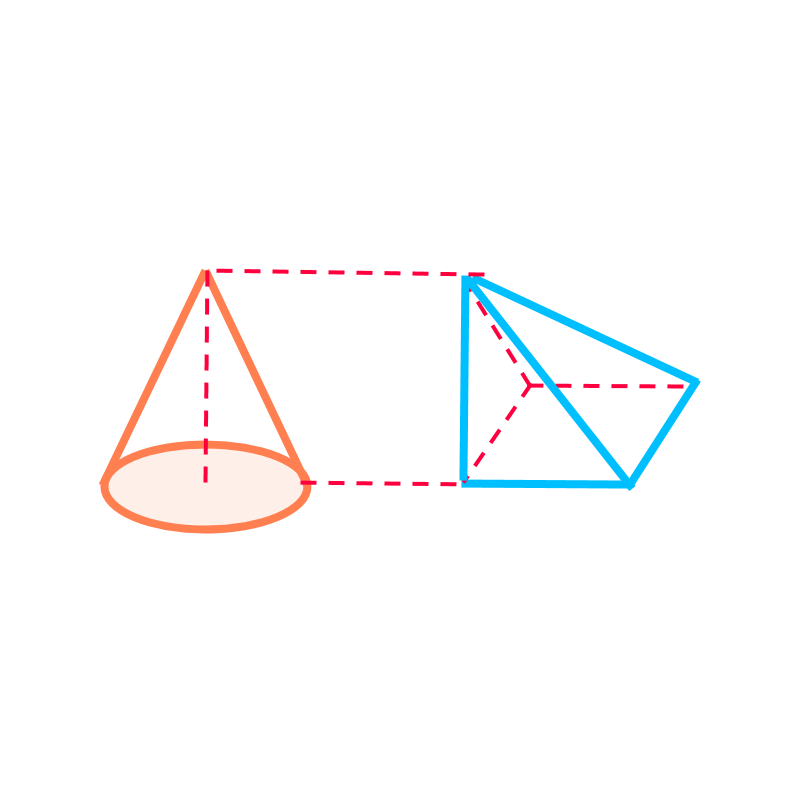$= 2 π r (r + l)$ $= 2pi r(r+l)$ Volume of a cone
$= \frac{1}{3} \times area of the base-face \times height$ $= 1/3 xx text( area of the base-face ) xx text( height)$

$= \frac{1}{3} π r^{2} h$ $= 1/3 pi r^2 h$

maths > mensuration-high > surface-area-volume-sphere

Sphere : Surface Area and Volume

In this page, finding surface area and volume of sphere is explained.

Surface Area and Volume of Sphere : surface area of a sphere Surface Area 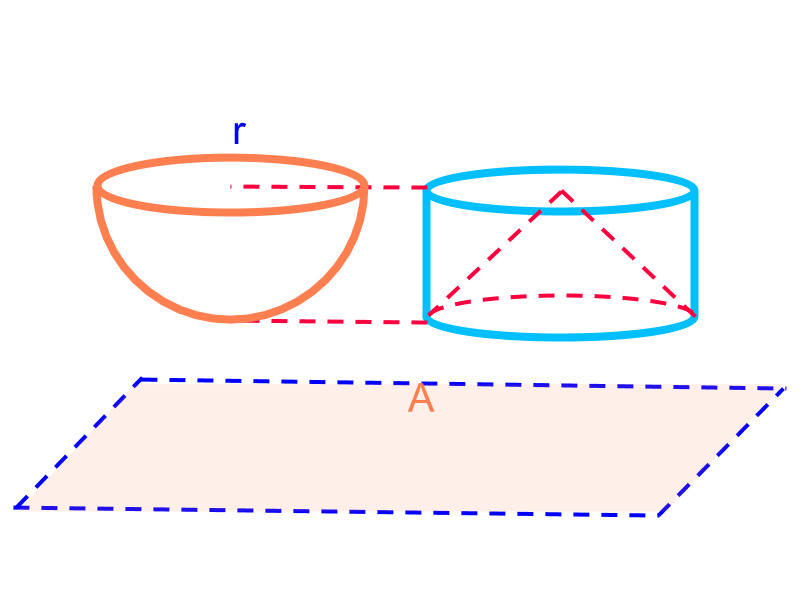$= 4 π r^{2}$ $= 4 pi r^2$ volume of a sphere Volume $= \frac{4}{3} π r^{3}$ $= 4/3 pi r^3$

maths > mensuration-high > understanding-part-shapes

Understanding Part Shapes

We studied about 2D shapes

• squares,

• rectangles,

• triangles,

• polygons, and

• circles These are some of the standard shapes.

Some part-shapes can be derived from these standard shapes. One of the method is to cut the shapes with straight lines and part of the standard shape is analyzed for perimeter or area. 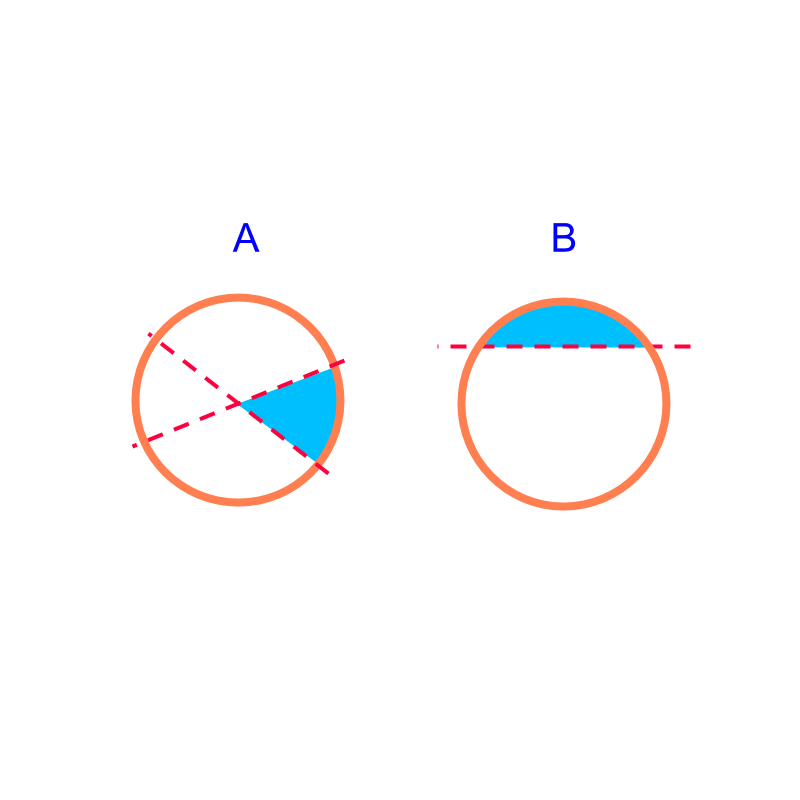sector and segment of a circle • the perimeter and area of sectors and segments. frustum of cone • the surface area and volume of frustum.

maths > mensuration-high > area-part-circle

Area of Parts of Circle : Sector and Segment

In this page, finding area of parts of circle, sectors and segments, is discussed. sector of a circle Arc Length and Area of a Sector: The arc-length and area are proportion to the angle subtended by the sector.

Arc length of a sector of $θ^{\circ}$ $theta^@$ angle $= 2 π r \times \frac{θ}{360}$ $=2 pi r xx theta/360$

Area of a sector of $θ^{\circ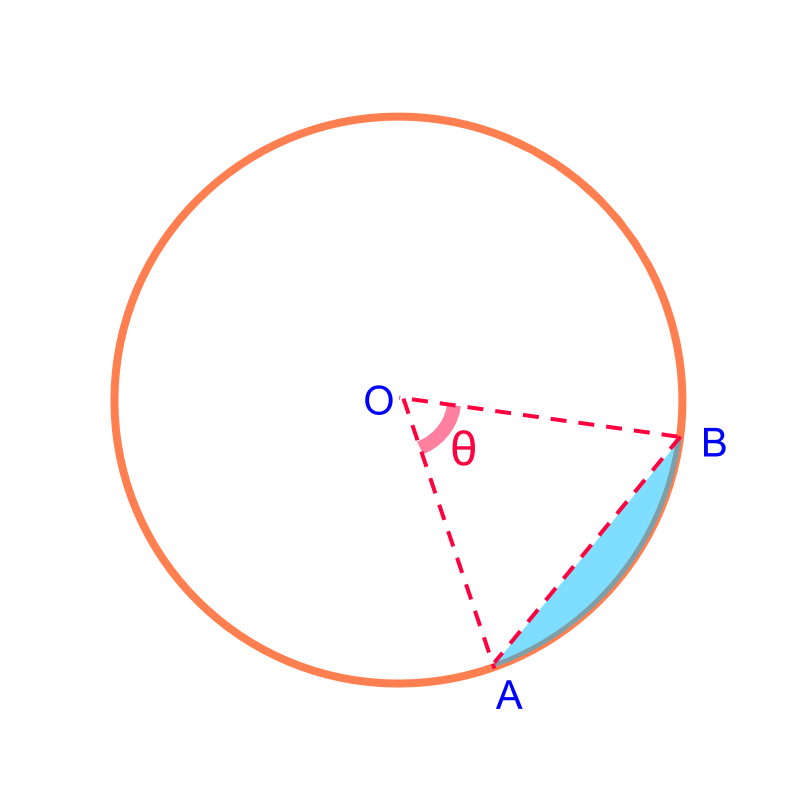}$ $theta^@$ angle $= π r^{2} \times \frac{θ}{360}$ $=pi r^2 xx theta/360$ segment of a circle Area of a Segment: is the difference between area of sector and the triangle.
Area of a Segment of $θ^{\circ}$ $theta^@$ angle = area of the corresponding sector $-$ $-$ the triangle

maths > mensuration-high > area-volume-frustum-cone

Surface Area and Volume of Frustum of a Cone

In this page, finding area and volume of a frustum, is discussed. frustum Surface Area and Volume of a frustum: The frustum is visualized as part of a cone and the height of the cone is worked out from the given height and radius of frustum.

Surface Area of frustum is the difference between surface area of larger cone and smaller cone.
$= π (r_{1} + r_{2}) \sqrt{h^{2} + {(r_{2} - r_{1})}^{2}}$ $=pi (r_1+r_2) sqrt(h^2+(r_2-r_1)^2)$

Volume of frustum is the difference between volume of larger cone and smaller cone.
$= \frac{1}{3} π h (r_{1}^{2} + r_{2}^{2} + r_{1} r_{2})$ $=1/3 pi h (r_1^2 + r_2^2 + r_1r_2)$