Mensuration : Length, Area, and Volume : Sphere : Surface Area and Volume

maths > mensuration-high

Sphere : Surface Area and Volume

what you'll learn...

Overview

Surface Area and Volume of Sphere : surface area of a sphere Surface Area $= 4 π r^{2}$ $= 4 pi r^2$ volume of a sphere Volume $= \frac{4}{3} π r^{3}$ $= 4/3 pi r^3$

sphere

The solid shape in the figure is "sphere". Sphere is a 3D solid with a center and a curved surface. Every point on the curved surface is in equal distance from the center.

surface area

The surface area of a sphere of radius $r$ $r$ is " $4 π r^{2}$ $4pi r^2$ ". This formula is explained below.

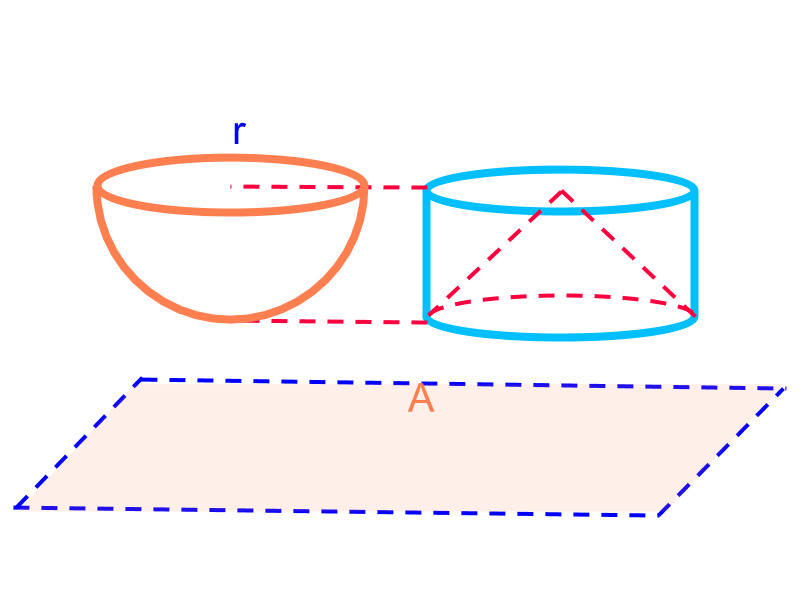
Note: To find the surface area of a sphere, the method "measurement by equivalence" is used. The surface area of sphere of radius $r$ $r$ is equivalent to the curved surface area of a cylinder of radius $r$ $r$ and height $2 r$ $2r$ .

A sphere of radius $r$ $r$ is shown in orange. A cylinder of height $2 r$ $2r$ and radius $r$ $r$ is shown in purple. A thin slice of sphere is taken at a vertical position. The surface area of the slice on the sphere equals the surface area of the corresponding slice on the cylinder.

To understand this consider the following figure.
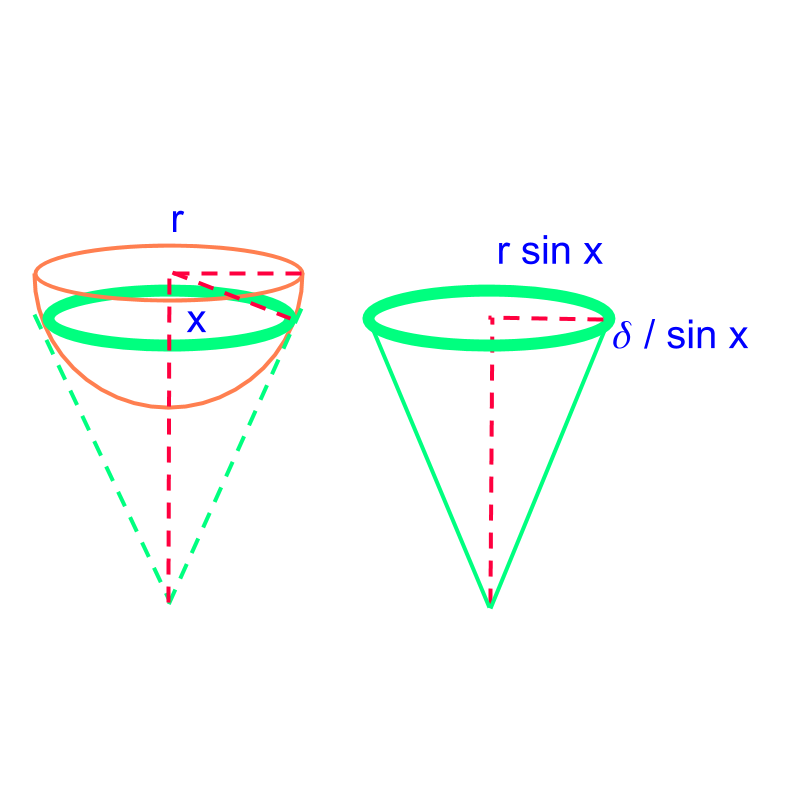
surface area of sphere
The thin strip is shown in green. The tangent on the position of thin strip makes a cone. The radius at that position is $r \sin x$ $r sin x$ and the height of the strip is $δ / \sin x$ $delta // sin x$ , where $x$ $x$ is the angle from the vertical axis of the sphere to the point of the strip, as shown in the figure.

Surface area of the sphere:

$= 2 \times$ $= 2 xx$ Surface area of the hemi-sphere:

$= 2 \times$ $=2 xx$ sum of surface area of strips of height $δ$ $delta$

$= 2 \times$ $= 2 xx$ sum of $π (r \sin x + r \sin x) δ / \sin x$ $pi (r sin x + r sin x) delta // sin x$

$= 2 \times$ $= 2 xx$ sum of $2 π r δ$ $2pi r delta$

$= 4 π r \times (sum of δ)$ $= 4 pi r xx (text( sum of )delta)$

$= 4 π r \times r$ $= 4 pi r xx r$

$= 4 π r^{2}$ $= 4 pi r^2$

volume

The volume of a sphere of radius $r$ $r$ is " $\frac{4}{3} π r^{3}$ $4/3 pi r^3$ ".

Note: To find the volume of a sphere, Cavalieri's principle in 3D is used. The volume of hemisphere is calculated to be $\frac{2}{3} π r^{3}$ $2/3 pi r^3$ . This formula is explained in the next page.

A hemi-sphere of radius $r$ $r$ is shown in orange. A cylinder of height $r$ $r$ and radius $r$ $r$ is shown in blue. A cone is visualized within the cylinder as shown in dotted line. A cross-section of sphere is taken at a vertical position. The area of the cross section of the sphere equals the area of the corresponding cross section of the cylinder excluding the cross-section of cone.

As per Cavalieri's principle in 3D, volume of the hemi-sphere:

$=$ $=$ volume of cylinder $-$ $-$ volume of the cone

$= π r^{3} - \frac{1}{3} π r^{3}$ $= pi r^3 - 1/3 pi r^3$

$= \frac{2}{3} π r^{3}$ $=2/3 pi r^3$

So the volume of the sphere is $\frac{4}{3} π r^{3}$ $4/3 pi r^3$

What is the volume of a hemi-sphere of radius $2$ $2$ cm?

The answer is " $\frac{2}{3} \times \frac{22}{7} \times 2 \times 2 \times 2 = 352 / 21$ $2/3 xx 22/7 xx 2 xx 2 xx 2 = 352//21$ $= 352 / 21$ $= 352//21$ "

summary

Surface Area and Volume of Sphere : surface area of a sphere Surface Area $= 4 π r^{2}$ $= 4 pi r^2$ volume of a sphere Volume $= \frac{4}{3} π r^{3}$ $= 4/3 pi r^3$

Outline

The outline of material to learn Mensuration : Length, Area, and Volume is as follows.

Note 1: click here for the detailed overview of Mensuration High

Note 2: click here for basics of mensuration, which is essential to understand this.

• Basics of measurement

→ Summary of Measurement Basics

→ Measurement by superimposition

→ Measurement by calculation

→ Measurement by equivalence

→ Measurement by infinitesimal pieces

→ Cavalieri's Principle (2D)

→ Cavalieri's Principle (3D)

• Perimeter & Area of 2D shapes

→ Circumference of Circles

→ Area of Circles

• Surface area & Volume of 3D shapes

→ Prisms : Surface Area & Volume

→ Pyramids : Surface Area & Volume

→ Cone : Surface Area & Volume

→ Sphere : Surface Area & Volume

• Part Shapes

→ Understanding part Shapes

→ Circle : Sector and Segment

→ Frustum of a Cone