Mensuration : Length, Area, and Volume : Equivalence by Infinitesimal Pieces

maths > mensuration-high

Equivalence by Infinitesimal Pieces

what you'll learn...

Overview

Equivalence by Infinitesimal Pieces : Length, Area, and Volume can be measured by equivalence with infinitesimal pieces. area by equivalence An example of finding perimeter of a circle is illustrated in the figure. The circle is spanned with isosceles triangles.

Approximate value of the perimeter of the circle equals sum of the bases of the triangles.

Accurate value of the perimeter of the circle is calculated by making the triangles infinitesimal small.

illustrating a problem

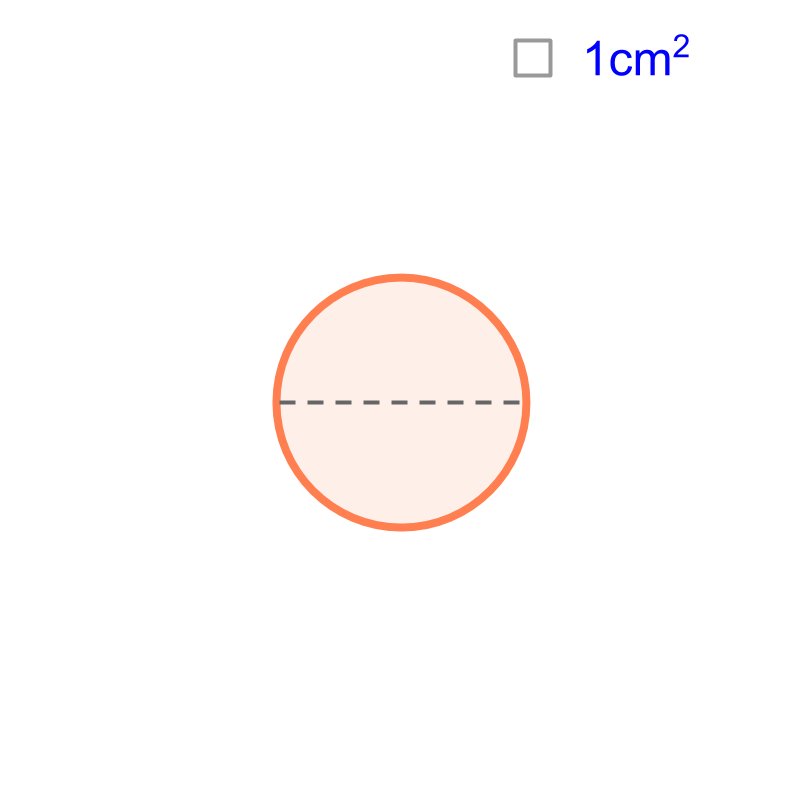
Consider the circle given in the figure. The diameter of the circle is $7$ $7$ cm. Can the perimeter of the circle be accurately calculated by superimposition? "Only approximate value is possible". As the length of unit-line is made finer, the accuracy would increase.

approximate

The circle is overlapped with triangles. Two sides of the triangles equal to the radius of the circle, and the third side (referred as base) is along the curved line of the given circle. The figure shows $10$ $10$ such triangles occupying a quarter of the circle. It is visualized that the three other quarters are also filled with triangles.

The length of the base of the triangles are added. This length will not be accurately equal to the perimeter of the circle. It is approximate. The base of triangles are straight lines but the section of circle is curved. The length of the base (which lies on the circle) will be little less than the length of the curved section.

increase accuracy

The question is "How to increase the accuracy of the perimeter value?"

If the triangle is made thinner (angle between equal sides is smaller), then the accuracy increases. Thus, the perimeter of the circle is found to be $3.14159 \dots$ $3.14159cdots$ by approximating the circle to infinitesimally small triangular pieces.

answer for unit-circle

The perimeter of a circle is calculated by one of many methods involving equivalence and approximation. For now, consider the diameter to be $1$ $1$ cm.

The perimeter of the circle is found to be $3.14159 \dots$ $3.14159cdots$ by approximating the circle to infinitesimally small triangular pieces.

Remember we studied that length of a line-segment can be measured finer and finer to an accurate value -- a decimal number that does not terminate and does not repeat. Similarly, the perimeter of a circle is a decimal number that does not terminate and does not repeat.

The perimeter of a circle of diameter $1$ $1$ cm is commonly approximated to a value $\frac{22}{7}$ $22/7$ or $3.14$ $3.14$ .

To represent the accurate decimal value, the number is represented with the symbol $π$ $pi$ . It is an irrational number or a decimal number that does not end or repeat.

answer for a circle

The perimeter of a circle with diameter $1$ $1$ cm is computed as a value represented with $π$ $pi$ .

What will be the perimeter of a circle with diameter $2$ $2$ cm or $20$ $20$ cm? Will there be more numbers like $π$ $pi$ ?

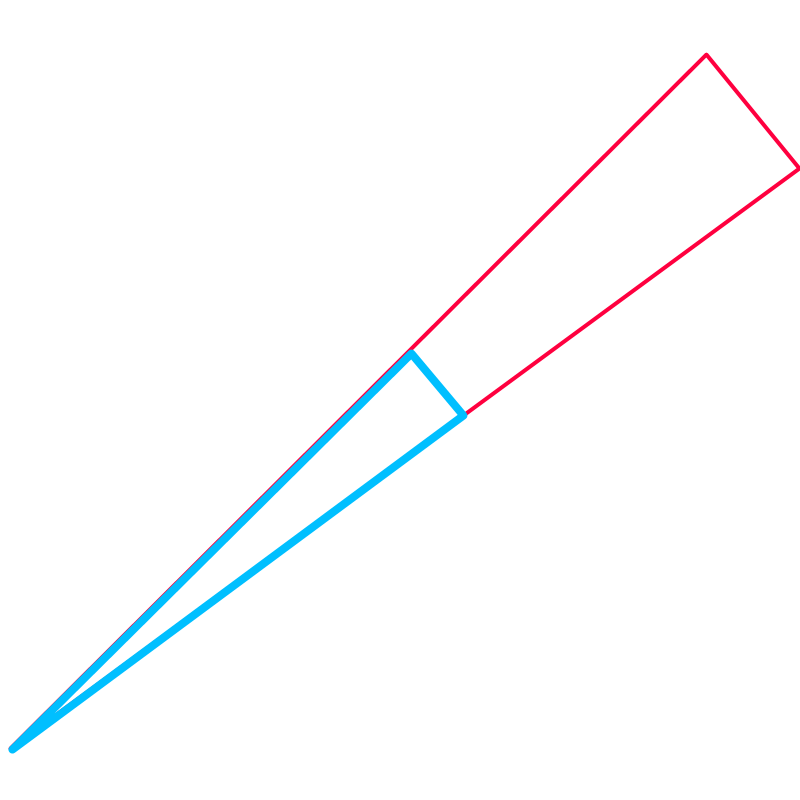
The question is answered with some geometrical calculations. Consider one piece of the triangle that was used to calculate perimeter of a circle of diameter $1$ $1$ cm. The triangle is shown in blue color in the figure.

The corresponding triangle for a perimeter $d$ $d$ cm is shown in red. Note that the triangles overlap and the blue triangle is shown on top of the red one.

The corresponding angles of these two triangles are equal and thus the triangles are similar triangles. One of the properties of similar triangles is that, "the ratio of corresponding sides are constant"

One of the triangles making a circle of $1$ $1$ cm diameter is shown in blue. And one of the triangles making a circle of $d$ $d$ cm diameter is shown in red. These triangles are similar. The property of similar triangles is that, the ratio of the sides are constant.

The isosceles sides of blue triangle are $1 / 2$ $1//2$ cm and the base is $x$ $x$ .
The isosceles sides of red triangles are $d / 2$ $d//2$ cm and the base is $y$ $y$ .

As per property of similar triangles,
$1 / 2 \div 1 / d = x \div y$ $1//2 -: 1//d = x -:y$
$\to y = d \times x$ $-> y=d xx x$
This means, the base of triangles from larger circle are $d$ $d$ times the base of triangles from smaller circle.
This implies that, the perimeter of larger circle of $d$ $d$ cm diameter is $d$ $d$ times the perimeter of the smaller circle.
The perimeter of the smaller circle of $1$ $1$ cm diameter is $π$ $pi$ .

This implies that "perimeter of the larger circle is $d \times π$ $d xx pi$ ".

summary

Outline

The outline of material to learn Mensuration : Length, Area, and Volume is as follows.

Note 1: click here for the detailed overview of Mensuration High

Note 2: click here for basics of mensuration, which is essential to understand this.

• Basics of measurement

→ Summary of Measurement Basics

→ Measurement by superimposition

→ Measurement by calculation

→ Measurement by equivalence

→ Measurement by infinitesimal pieces

→ Cavalieri's Principle (2D)

→ Cavalieri's Principle (3D)

• Perimeter & Area of 2D shapes

→ Circumference of Circles

→ Area of Circles

• Surface area & Volume of 3D shapes

→ Prisms : Surface Area & Volume

→ Pyramids : Surface Area & Volume

→ Cone : Surface Area & Volume

→ Sphere : Surface Area & Volume

• Part Shapes

→ Understanding part Shapes

→ Circle : Sector and Segment

→ Frustum of a Cone