Statistics & Probability : Introduction to Grouped Data

maths > statistics-basics

Introduction to Grouped Data

what you'll learn...

overview

In this page, grouped data is introduced and explained with some examples.

recap

We studied about data recording and presentation with tally marks and tabular form. Then we studied about bar-graphs to represent the data in a spatially laid-out form which helps to compare data or find the minimum or maximum, etc.

it works

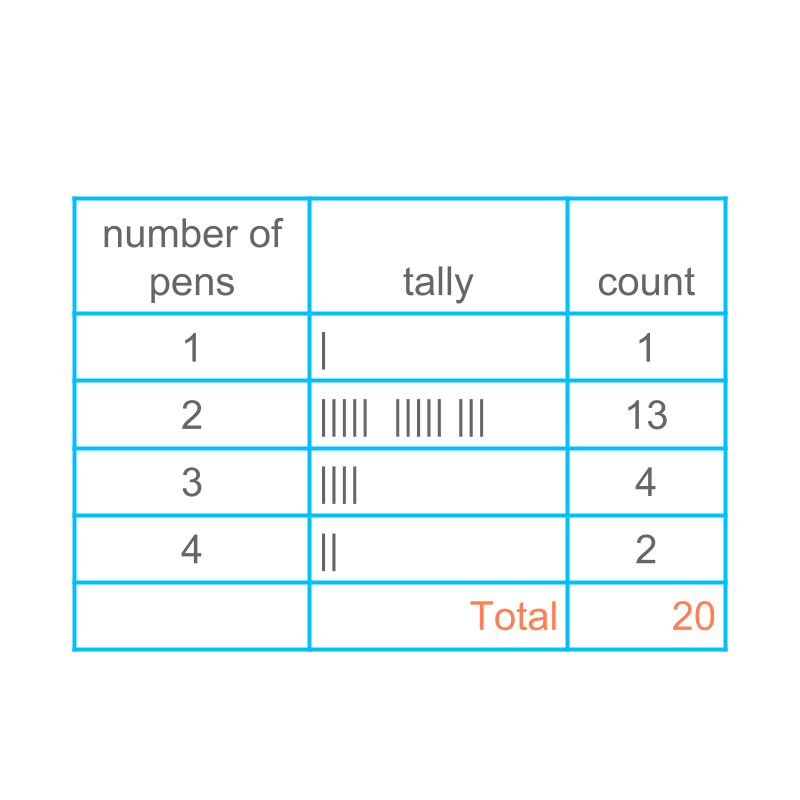
Consider the number of pens a student carries in a group of $20$ $20$ students. The raw data is given as :

   $2$ $2$ , $1$ $1$ , $2$ $2$ , $4$ $4$ , $2$ $2$
   $3$ $3$ , $2$ $2$ , $2$ $2$ , $2$ $2$ , $3$ $3$
   $3$ $3$ , $2$ $2$ , $2$ $2$ , $3$ $3$ , $2$ $2$
   $2$ $2$ , $2$ $2$ , $4$ $4$ , $2$ $2$ , $2$ $2$

The figure provides the tally and tabular representation of the given raw data.

it does not work

Consider the data height of students in a class of $20$ $20$ students.

   $90.2$ $90.2$ , $97.4$ $97.4$ , $99.7$ $99.7$ , $88.3$ $88.3$ , $90.7$ $90.7$

   $93.5$ $93.5$ , $96.8$ $96.8$ , $89.5$ $89.5$ , $99.5$ $99.5$ , $98.9$ $98.9$

   $91.2$ $91.2$ , $101.3$ $101.3$ , $94.0$ $94.0$ , $93.4$ $93.4$ , $93.1$ $93.1$

   $94.7$ $94.7$ , $96.9$ $96.9$ , $92.8$ $92.8$ , $91.8$ $91.8$ , $99.6$ $99.6$

Note that none of the data values repeat, and there are $20$ $20$ distinct values. If we are to prepare tally form of the data, each data point would get one bar.
Can the data be presented in tally and table form? Not as it is given.

make it work

The data will not be used to answer questions like "How many students are of the height $95$ $95$ cm?" The answer to this kind of questions is always none.

The data is primarily used to answer questions similar to

How many students are in the range $90$ $90$ to $95$ $95$ cm height? (which is as per the normal height for the age.)

How many students are below the lower limit $90$ $90$ cm? (Which is below the healthy height for the age.)

How many students are above $100$ $100$ cm ?

To cater to this, the data can be grouped into small segments of the data values. 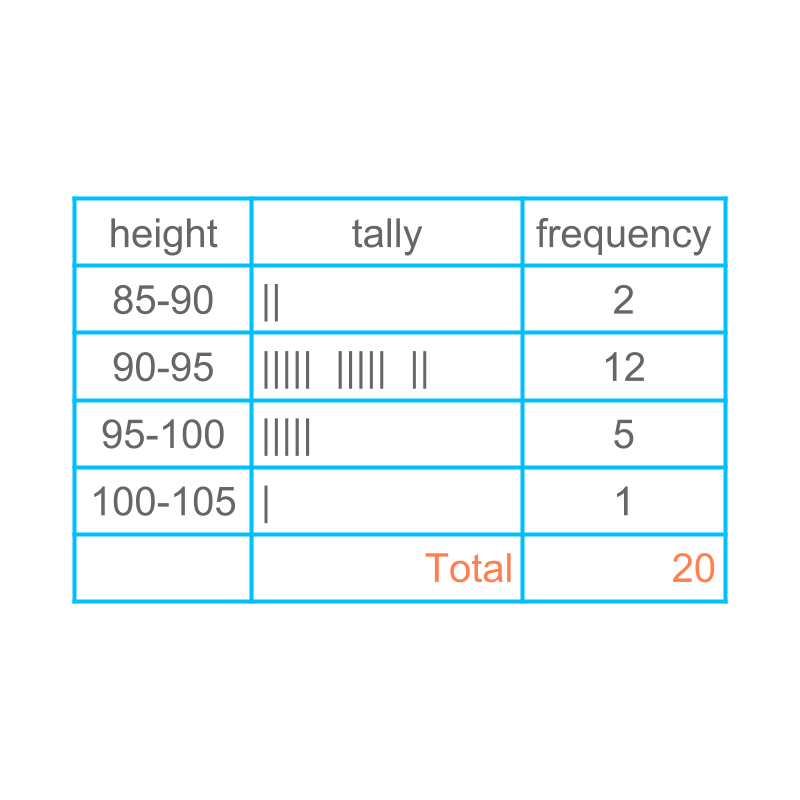grouping of data in tabular form The figure illustrates the tally and table form of grouped data. The data is grouped as

   less than $90$ $90$

   $90$ $90$ to $95$ $95$

   $95$ $95$ to $100$ $100$

   above $100$ $100$

make bargraph work too

Considering the data: height of students in a class of $20$ $20$ students.

Bar-graph are usually defined for distinct values: eg: $2$ $2$ , $3$ $3$ , etc.

The data in figure is continuous ranges : eg $90$ $90$ to $95$ $95$ and $95$ $95$ to $100$ $100$ , etc.

This continuous scale be reflected in a bar-graph, by making the bars touching each other to reflect continuity.

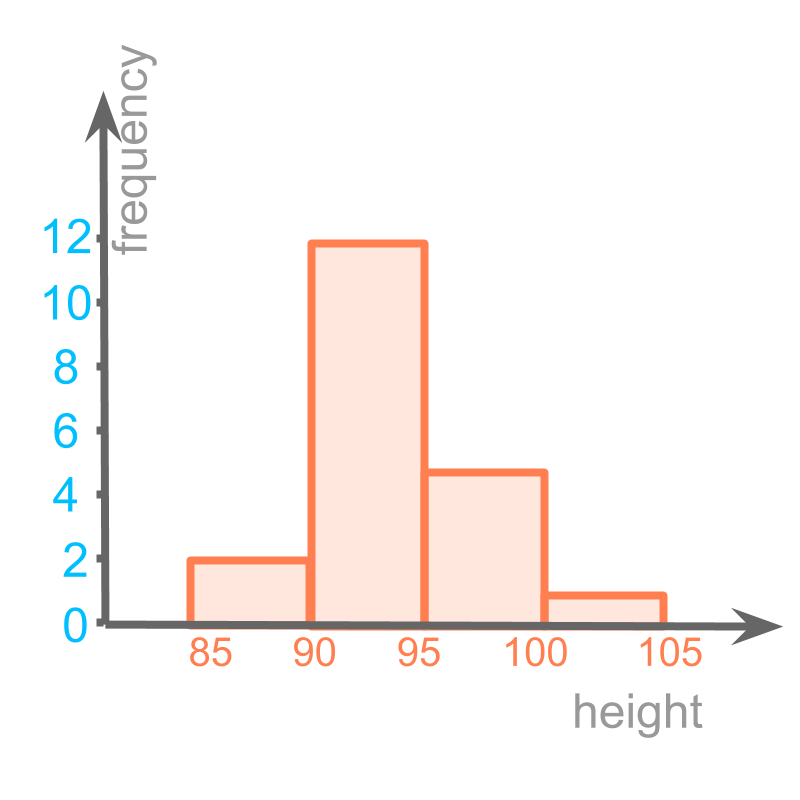
The bar graph with continuous range is shown in the figure.

This form of bar-graph is called "histogram".

The word "histogram", means written or recorded information in the form of vertical bars".

"-gram" : written or recorded information + "histo" : in the form of vertical bars.

different possibilities in grouping

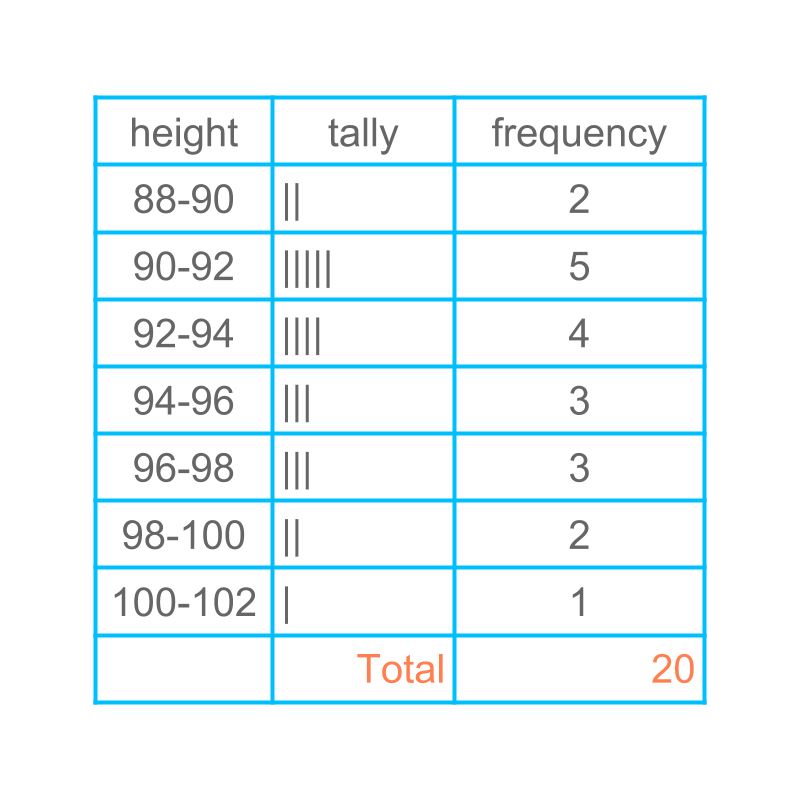
Considering the data height of students in a class of $20$ $20$ students. A different grouping is presented in the figure.

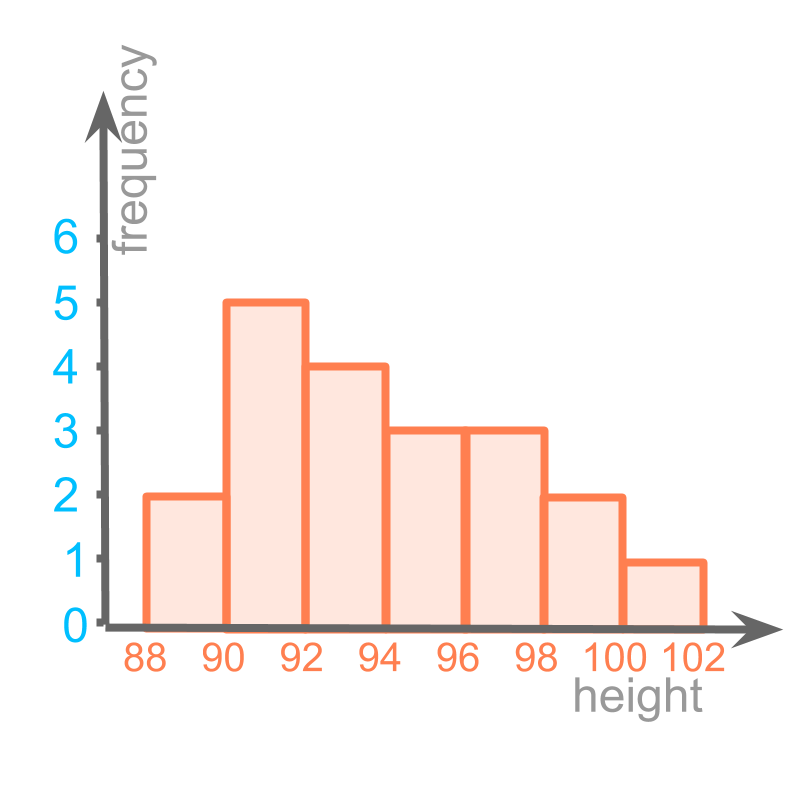
Histogram of the same is given in the figure.

summary

Grouped data : Data can be grouped into small segments of the data values. grouping of data in tabular form The figure illustrates the tally and table form of grouped data.

Histrogram : A representation of data similar to bar-graph with continuous scale on the horizontal axis.

Outline

The outline of material to learn "basics of statistics and probability" is as follows.

Note: Click here for detailed outline of "Basics of Statistics and Probability"

• Introduction

→ Introduction to Statistics

→ Organizing Data : Tally Table

→ Pictograph

→ Bargraph

• Data Analysis

→ Cumulative Frequency

→ Representative Values of Data

→ Central Tendencies

→ Bargraphs & Piecharts

• Probability Fundamentals

→ Predicting Future

→ Random Experiment

→ Probability

→ Standard Experiments

• Statistics Grouped Data

→ Grouped Data

→ Probability in Grouped Data

→ Class Parameters of Grouped Data

→ Methods to find Mean of Grouped data

→ Mode of Grouped data

→ Median of Grouped Data