Trigonometry (Introduction) : Understanding Standard Angles

maths > trigonometry

Understanding Standard Angles

what you'll learn...

Overview

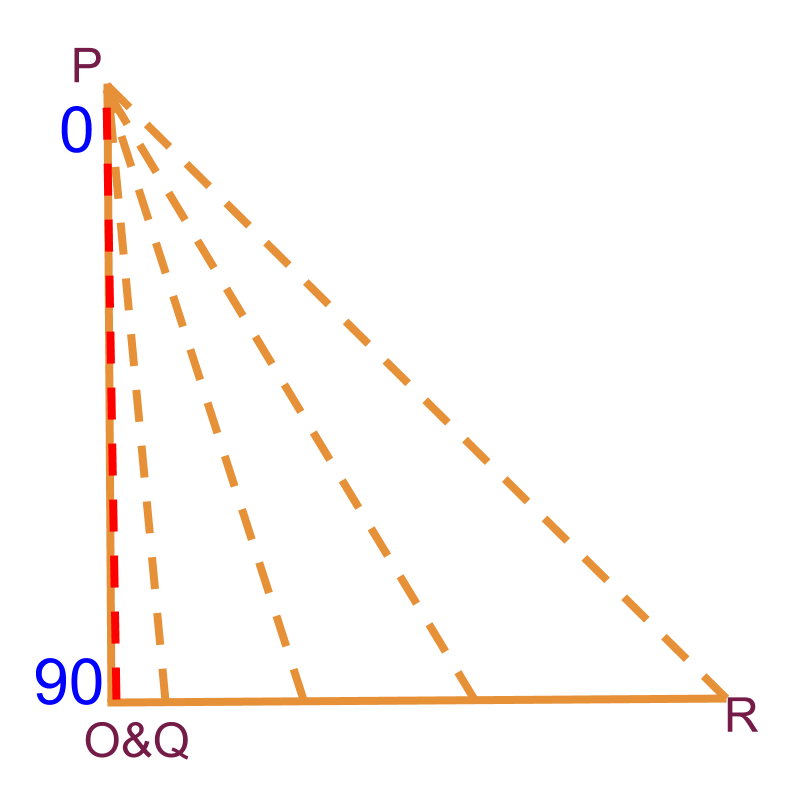
» 0 : minimum possible angle
→ opposite side is 0

» 90 : Maximum possible angle
→ opposite side equals hypotenuse

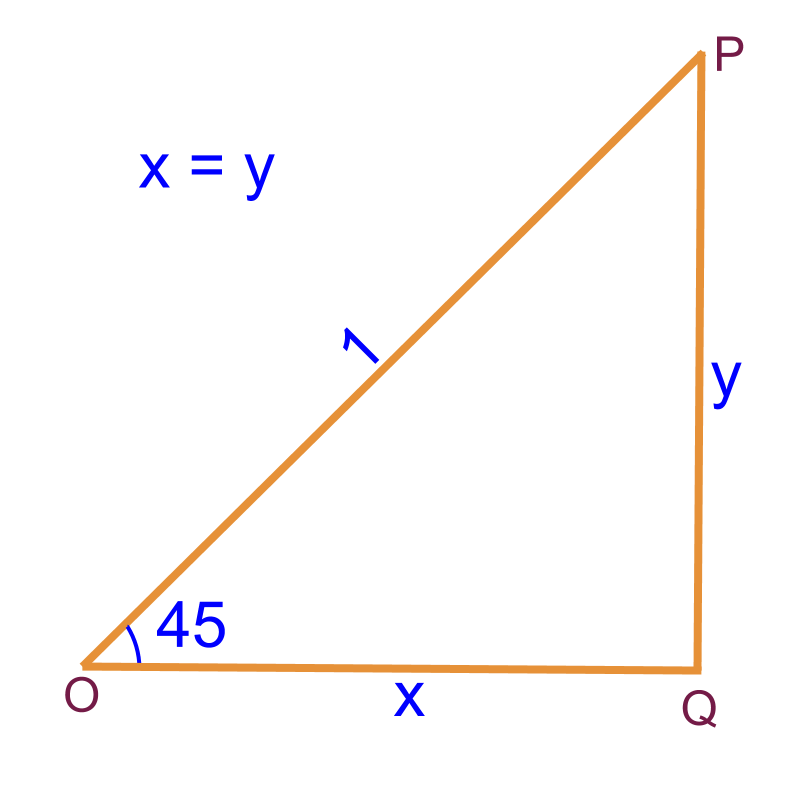
» 45 : isosceles right-triangle
→ opposite and adjacent sides equal

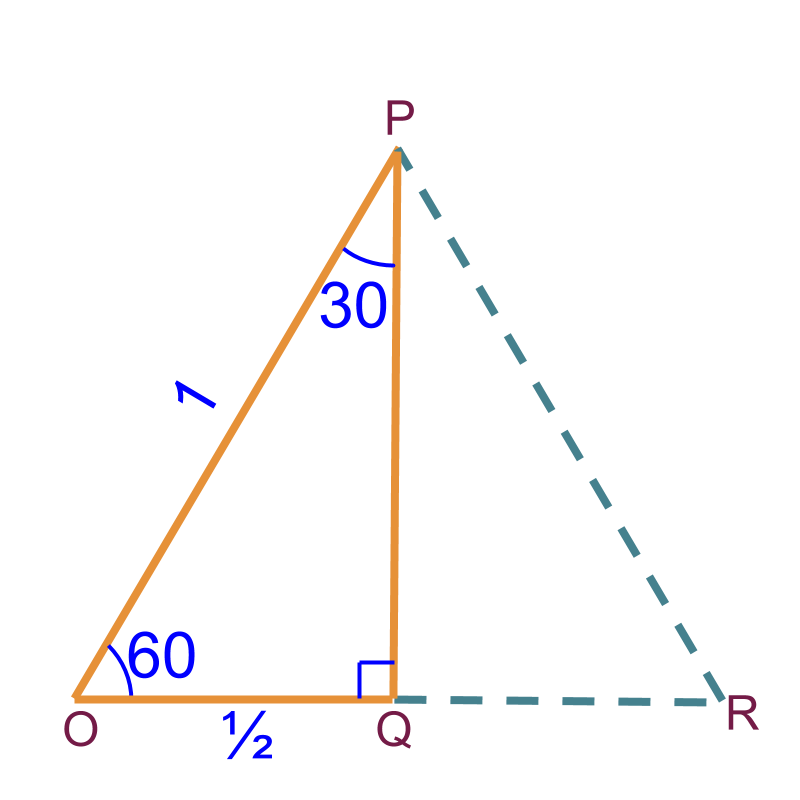
» 30 and 60 : Derived from equilateral triangle
→ one side is half of hypotenuse

equilateral, isosceles, zero degree

We had studied that the ratio of two sides of a right-triangle is a constant and the such constants are named $\sin θ, \cos θ, \dots$ $sin theta, cos theta, cdots$ for given values of $θ = 0^{\circ}, {0.2}^{\circ}, 1^{\circ}, {2.7}^{\circ}, \dots$ $theta = 0^@, 0.2^@, 1^@, 2.7^@, cdots$ .

It is noted that one cannot memorize all values of $\sin θ$ $sin theta$ . A reference table is to be created and used when required.

Students work out values of trigonometric ratios $\sin$ $sin$ , $\cos$ $cos$ , and $\tan$ $tan$ , for the angles for which the ratio between two sides of triangles can be computed using only given angle

The ratio between two sides of triangles be computed for the following

• equilateral triangles

• isosceles triangles

• triangles with one angle $0^{\circ}$ $0^@$

equilateral

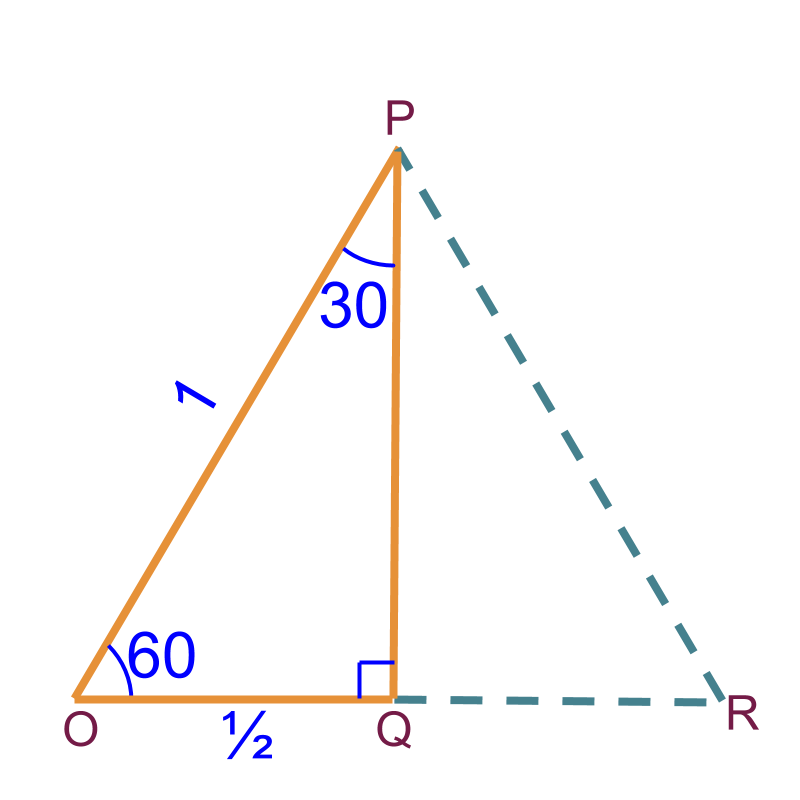
The equilateral triangle is split into two right angled triangles as shown in the figure. The hypotenuse $\bar{O P} = 1$ $bar(OP) = 1$ . Then the side $\bar{O Q} = \frac{1}{2}$ $bar(OQ) = 1/2$ . The other side is to be computed using Pythagoras Theorem.

The standard angles in this triangles are $60^{\circ}$ $60^@$ and $30^{\circ}$ $30^@$

isosceles

The two sides of the isosceles right angled triangle are same and the hypotenuse is $1$ $1$ .

The standard angle derived from isosceles right-angled-triangles is $45^{\circ}$ $45^@$ .

zero degree

trigonometry standard angles from triangle with 0 degree

The figure shows a triangle $Δ O P Q$ $Delta OPQ$ with $∠ P = 0^{\circ}$ $/_P = 0^@$ . Imagine the $\bar{P R}$ $bar(PR)$ moves towards $\bar{P O}$ $bar(PO)$ and forms the triangle where point $R$ $R$ meets point $O$ $O$ .

The standard angles in a right-angled triangle with one of the angles $0^{\circ}$ $0^@$ are $0^{\circ}$ $0^@$ and $90^{\circ}$ $90^@$ .

The word "standard" means: common and established as norm.

Summary

The standard angles for which the trigonometric ratios are in the form of simple ratios, are derived from equilateral, isosceles, and $0^{\circ}$ $0^@$ triangles. Use the known properties of these triangles to compute the trigonometric values for the standard angles.

Trigonometric Ratios for Standard Angles:

• $0^{\circ}$ $0^@$ and $90^{\circ}$ $90^@$ : right-angled-triangle with two sides $1$ $1$ and the third side $0$ $0$ .

• $45^{\circ}$ $45^@$ : isosceles right-angled triangle.

• $30^{\circ}$ $30^@$ and $60^{\circ}$ $60^@$ : half of equilateral triangle making a right-angled-triangle.

Outline

The outline of material to learn "Basics of Trigonometry" is as follows.

• Detailed outline of "trigonometry".

→ Basics - Angles

→ Basics - Triangles

→ Importance of Right Angled Triangle

→ Trigonometric Ratio (Basics)

→ Triangular Form of Trigonometric Ratios

→ Introduction to Standard Angles

→ Trigonometric Ratio of Standard Angles

→ Trigonometric Identities

→ Trigonometric Ratios of Complementary Angles