Trigonometry (Introduction) : Basics of Triangles

maths > trigonometry

Basics of Triangles

what you'll learn...

Overview

» Congruent Triangles: Triangles that are identical.

» Similar Triangles: Triangles that are scaled.

» Right-Triangle: A triangle with one angle $90^{\circ}$ $90^@$ .

» 3 independent parameters in a triangle
    → angle-side-angle
    → side-side-side
    → side-angle-side
    → angle-angle-side
    → (angle-angle-angle are not independent)
    → (side-side-angle leads to 2 possibilities)

» 2 independent parameters in a right-triangle
→ side-angle
→ side-side

» 1 independent parameter in "class of similar-right-triangles"
→ angle

Congruent, Similar, right-angled Triangles

The sum of all 3 interior angles of a triangle is $180^{\circ}$ $180^@$ .

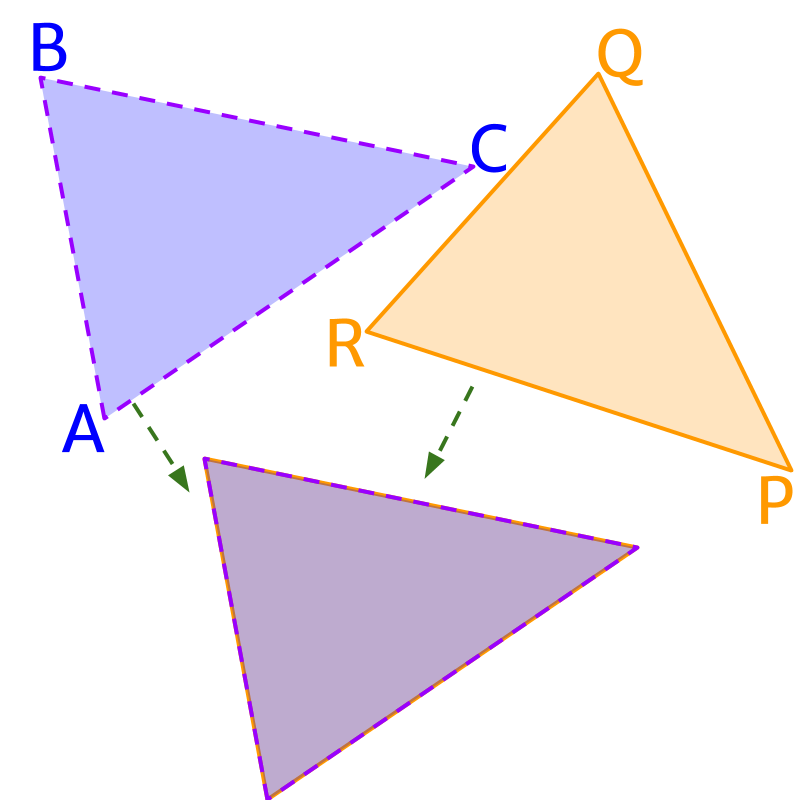
Congruent Triangles are triangles that are identical and exactly fit over another. Note triangles can be flipped or rotated while comparing.

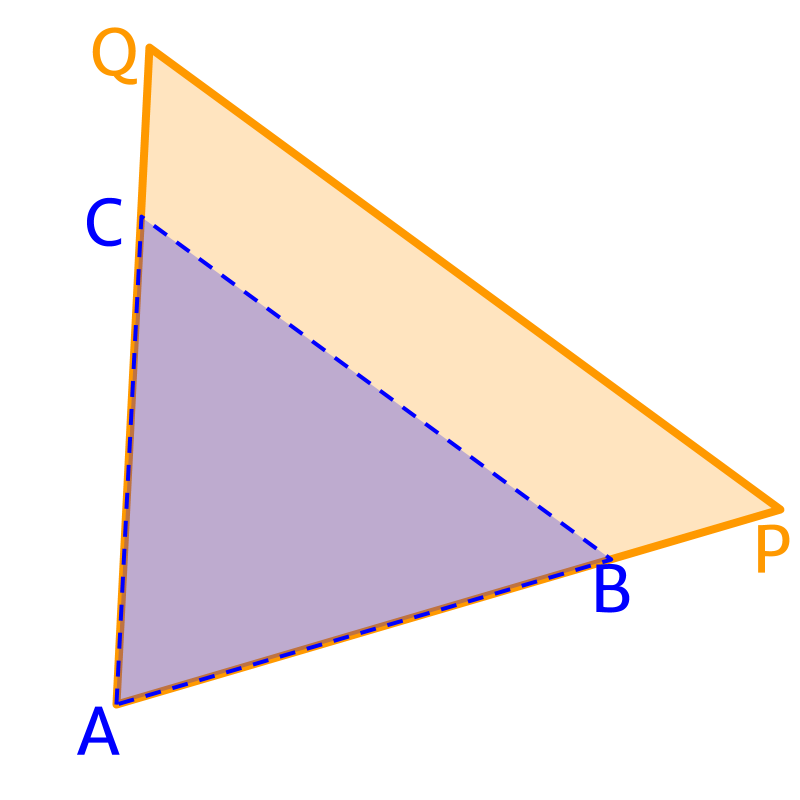
Similar triangles are triangles that have same shape or better defined as the triangles that are scaled up or down version of one another.

Right angled triangles are triangles with one angle $90^{\circ}$ $90^@$ . Right angled triangles can be called right-triangles.

Independent Parameters

A triangle has $3$ $3$ independent parameters.

For example, given that two sides of a triangle are $1$ $1$ , $1$ $1$ , and the angle between those two sides is $60^{\circ}$ $60^@$ , it is derived that the triangle is a equilateral triangle.

The combination of independent parameters are given as

• side-side-side

• side-angle-side

• angle-side-angle

• angle-angle-side

Note that, angle-angle-angle are not independent parameters as sum of angles in a triangle is $180^{\circ}$ $180^@$ . So given two angles, third angle can be calculated.

A right angled triangle is defined by $2$ $2$ independent parameters.

For a right angled triangle, one angle is given as $90^{\circ}$ $90^@$ , so the independent parameters are given

• side-side

• side-angle

The statement "two independent parameters define a right angled triangle" means the following. If two of $2$ $2$ angles (excluding the right angle) or $3$ $3$ sides are given, then all other angle or sides are exactly defined and mathematically computed.

The combination of two parameters are

Given side-side, the third side and two angles can be calculated.

Given angle-side, the other two sides and the angle can be calculated.

Pythagoras Theorem

The two arms to the right angle are given as $a$ $a$ and $b$ $b$ . Since two independent parameters define a right angled triangle, we should be able to compute the third side $c$ $c$ .

This is given as Pythagoras Theorem, $c = \sqrt{a^{2} + b^{2}}$ $c = sqrt(a^2+b^2)$ .

Pythagoras Theorem: It is understood that the two arms of right angled triangle defines the hypotenuse. As length of one arm changes, the hypotenuse also changes accordingly. The relationship between the arms and the hypotenuse is given by $a^{2} + b^{2} = c^{2}$ $a^2+b^2 = c^2$ .

This happens to be a cute expression and it is used often in mathematics. Thus, it is one of the most popular theorems. The explanations like $c^{2}$ $c^2$ represents area of square with hypotenuse as side etc. are proofs or analogies of this relationship.

The expression $a^{2} + b^{2} = c^{2}$ $a^2+b^2 = c^2$ , in the absolute sense, captures the relationship between two arms and the hypotenuse, as only two parameters are independent.

Similar Right Triangles

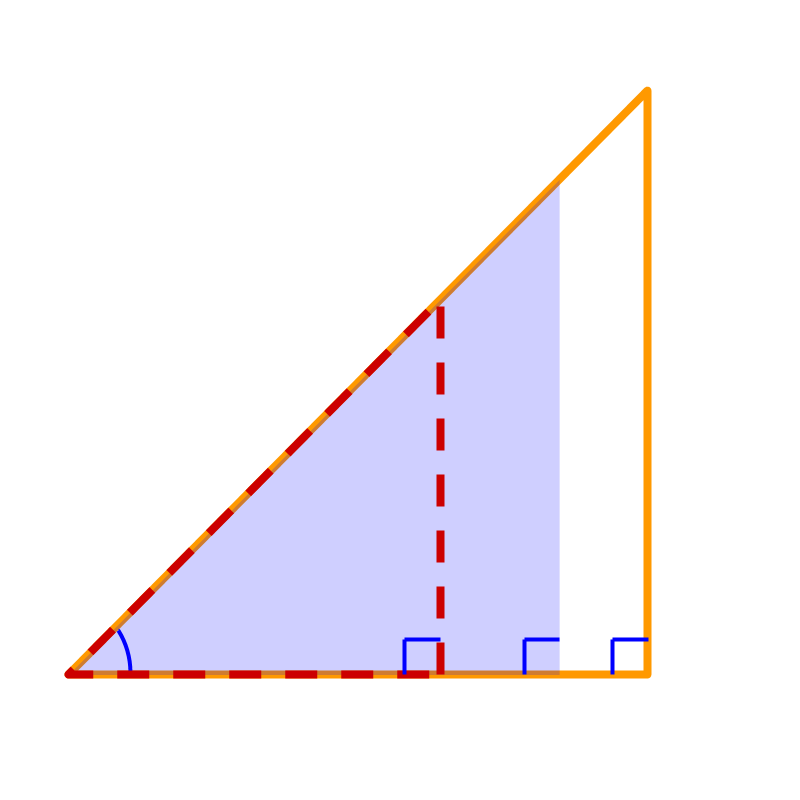
Set of similar right triangles is defined by one angle. That is the number of independent parameters is $1$ $1$ , which is an angle.

(Figure shows three triangles, solid line, dotted line, and shaded.)

Summary

Basics of Triangles to learn trigonometry :

• Congruent and Similar Triangles.

• three parameters define a triangle

• two parameters define a right angled triangle

• one parameter define set of similar right angled triangles : angle

Congruent Triangles: Triangles that are identical.

Similar Triangles: Triangles that are scaled and have same shape.

Right Angled Triangle: Triangles having one angle as $90^{\circ}$ $90^@$ .

Number of Parameters Defining a Triangle: Minimum three independent parameters are required to specify a triangle: SSS, SAS, ASA, AAS

Number of Parameters Defining a Right Angled Triangle: Minimum two independent parameters are required to specify a right angled triangle : SA or SS

Number of Parameters Defining set of Similar Right Angled Triangles: One parameter define set of similar right angled triangles : A

Pythagoras Theorem (defined in first principles): A right angled triangle is defined by two independent parameters. Hence, The three parameters, hypotenuse and the two legs, are related. The relationship is given by the expression
$a^{2} + b^{2} = c^{2}$ $a^2+b^2 = c^2$

where $c$ $c$ is the hypotenuse and $a$ $a$ and $b$ $b$ are the two legs.

Outline

The outline of material to learn "Basics of Trigonometry" is as follows.

• Detailed outline of "trigonometry".

→ Basics - Angles

→ Basics - Triangles

→ Importance of Right Angled Triangle

→ Trigonometric Ratio (Basics)

→ Triangular Form of Trigonometric Ratios

→ Introduction to Standard Angles

→ Trigonometric Ratio of Standard Angles

→ Trigonometric Identities

→ Trigonometric Ratios of Complementary Angles