Trigonometry (Introduction) : Trigonometric Ratios for Standard Angles

maths > trigonometry

Trigonometric Ratios for Standard Angles

what you'll learn...

Overview

» Quickly follow the angle description to calculate the ratios. No need to memorize.

isosceles right triangle : $45^{\circ}$ $45^@$

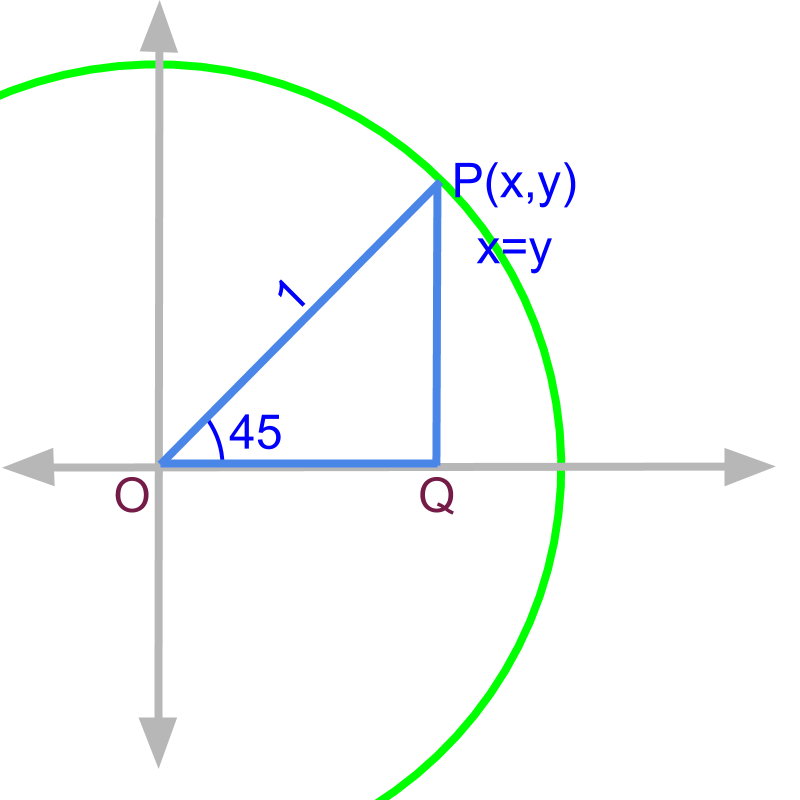
Given the right angled triangle $Δ O P Q$ $Delta OPQ$ , and $∠ P O Q = 45^{\circ}$ $/_POQ = 45^@$ .

$\bar{O P} = 1$ $bar(OP)= 1$
$\bar{O Q} = \bar{P Q} = x = y$ $bar(OQ)=bar(PQ)=x=y$
${\bar{O Q}}^{2} + {\bar{P Q}}^{2} = {\bar{O P}}^{2} = 1$ $bar(OQ)^2+bar(PQ)^2 = bar(OP)^2 = 1$

$2 x^{2} = 1$ $2 x^2 = 1$

The point P is $(\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$ $(1/sqrt(2), 1/sqrt(2))$ .

It is proven that point $P (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}})$ $P (1/sqrt(2), 1/sqrt(2))$ . That is,

opposite side $\bar{P Q} = \frac{1}{\sqrt{2}}$ $bar(PQ) = 1/sqrt(2)$

adjacent side $\bar{O Q} = \frac{1}{\sqrt{2}}$ $bar(OQ) = 1/sqrt(2)$

hypotenuse $\bar{O P} = 1$ $bar(OP) = 1$

${\sin 45}^{\circ} = \frac{1}{\sqrt{2}}$ $sin 45^@ = 1/sqrt(2)$

${\cos 45}^{\circ} = \frac{1}{\sqrt{2}}$ $cos 45^@ = 1/sqrt(2)$

${\tan 45}^{\circ} = 1$ $tan 45^@ = 1$

Do not memorize the trigonometric ratios, it is easy to work out the lengths of the three sides of a triangle of standard angles.

Once we know the lengths of the three sides, it is easy to work out the trigonometric ratios.

For example, ${\cot 45}^{\circ}$ $cot 45^@$ is $1$ $1$ (by finding ratio adjacent by opposite side).

equilateral triangle : $60^{\circ}$ $60^@$ and $30^{\circ}$ $30^@$

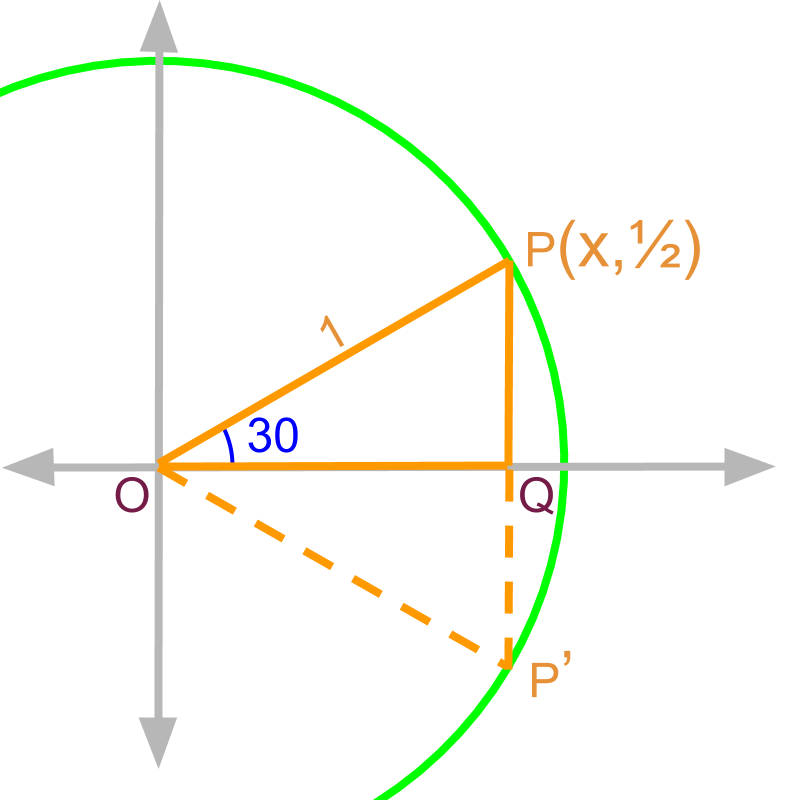
Given the right angled triangle $Δ O P Q$ $Delta OPQ$ , and $∠ P O Q = 30^{\circ}$ $/_POQ = 30^@$ .

$\bar{O P} = 1$ $bar(OP)= 1$
Construct an equilateral triangle $Δ O P' P$ $Delta OP′P$ .
From this, it is derived that $\bar{P Q} = \frac{1}{2}$ $bar(PQ)=1/2$ .
${\bar{O Q}}^{2} + {\bar{P Q}}^{2} = {\bar{O P}}^{2} = 1$ $bar(OQ)^2+bar(PQ)^2 = bar(OP)^2 = 1$

$x^{2} + {(\frac{1}{2})}^{2} = 1$ $x^2+(1/2)^2 = 1$

The point $P$ $P$ is $(\frac{\sqrt{3}}{2}, \frac{1}{2})$ $(sqrt(3)/2 , 1/2)$ .

It is proven that point $P (\frac{\sqrt{3}}{2}, \frac{1}{2})$ $P (sqrt(3)/2 , 1/2)$ . That is,

opposite side $\bar{P Q} = \frac{1}{2}$ $bar(PQ) = 1/2$

adjacent side $\bar{O Q} = \frac{\sqrt{3}}{2}$ $bar(OQ) = sqrt(3)/2$

hypotenuse $\bar{O P} = 1$ $bar(OP) = 1$

${\sin 30}^{\circ} = \frac{1}{2}$ $sin 30^@ = 1/2$

${\cos 30}^{\circ} = \frac{\sqrt{3}}{2}$ $cos 30^@ = sqrt(3)/2$

${\tan 30}^{\circ} = \frac{1}{\sqrt{3}}$ $tan 30^@ = 1/sqrt(3)$

It is noted that one does not need to memorize the trigonometric ratios, it is easy to work out the lengths of the three sides of a triangle of standard angles. Once we know the lengths of the three sides, it is easy to work out the trigonometric ratios.

For example, ${\sec 30}^{\circ} = \frac{2}{\sqrt{3}}$ $sec 30^@ = 2/sqrt(3)$

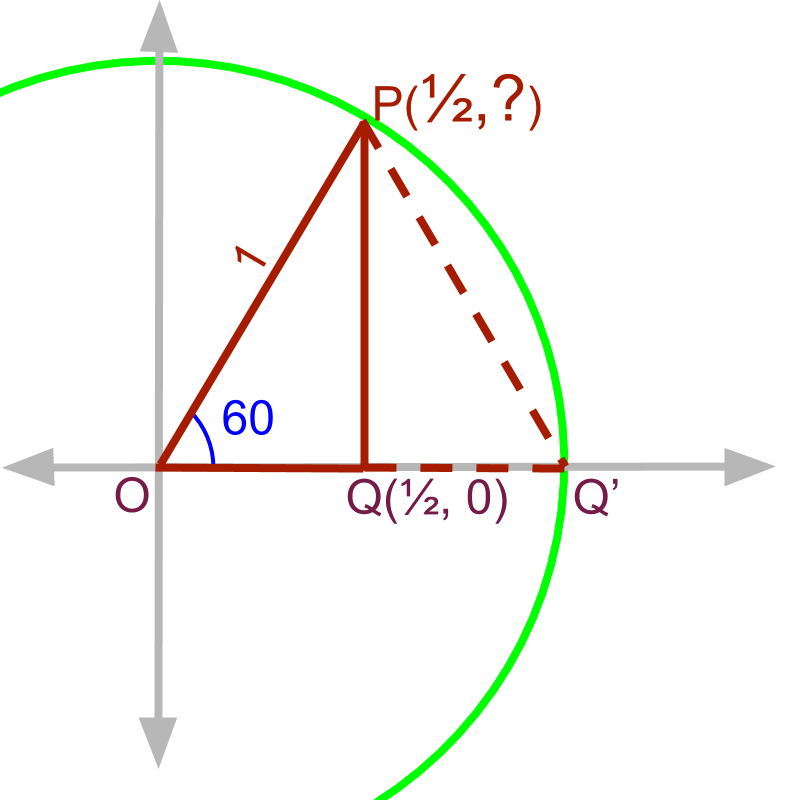
Given the right angled triangle $Δ O P Q$ $Delta OPQ$ , and $∠ P O Q = 60^{\circ}$ $/_POQ = 60^@$ .

$\bar{O P} = 1$ $bar(OP)= 1$
Construct an equilateral triangle $Δ O Q' P$ $Delta O Q′P$ .
From this, it is derived that $\bar{O Q} = \frac{1}{2}$ $bar(OQ)=1/2$ .
${\bar{O Q}}^{2} + {\bar{P Q}}^{2} = {\bar{O P}}^{2} = 1$ $bar(OQ)^2+bar(PQ)^2 = bar(OP)^2 = 1$

${(\frac{1}{2})}^{2} + y^{2} = 1$ $(1/2)^2+ y^2 = 1$

The point $P$ $P$ is $(\frac{1}{2}, \frac{\sqrt{3}}{2})$ $(1/2 , sqrt(3)/2)$ .

It is proven that point $P (\frac{1}{2}, \frac{\sqrt{3}}{2})$ $P (1/2 , sqrt(3)/2)$ . That is,

opposite side $\bar{P Q} = \frac{\sqrt{3}}{2}$ $bar(PQ) = sqrt(3)/2$

adjacent side $\bar{O Q} = \frac{1}{2}$ $bar(OQ) = 1/2$

hypotenuse $\bar{O P} = 1$ $bar(OP) = 1$

${\sin 60}^{\circ} = \frac{\sqrt{3}}{2}$ $sin 60^@ = sqrt(3)/2$

${\cos 60}^{\circ} = \frac{1}{2}$ $cos 60^@ = 1/2$

${\tan 60}^{\circ} = \sqrt{3}$ $tan 60^@ = sqrt(3)$

It is repeated that one does not need to memorize the trigonometric ratios, it is easy to work out the lengths of the three sides of a triangle of standard angles and thus the ratios.

For example, the $cosec 60^{\circ} = \frac{2}{\sqrt{3}}$ $text(cosec) 60^@ = 2/sqrt(3)$

Right Triangle with $0^{\circ}$ $0^@$ and $90^{\circ}$ $90^@$

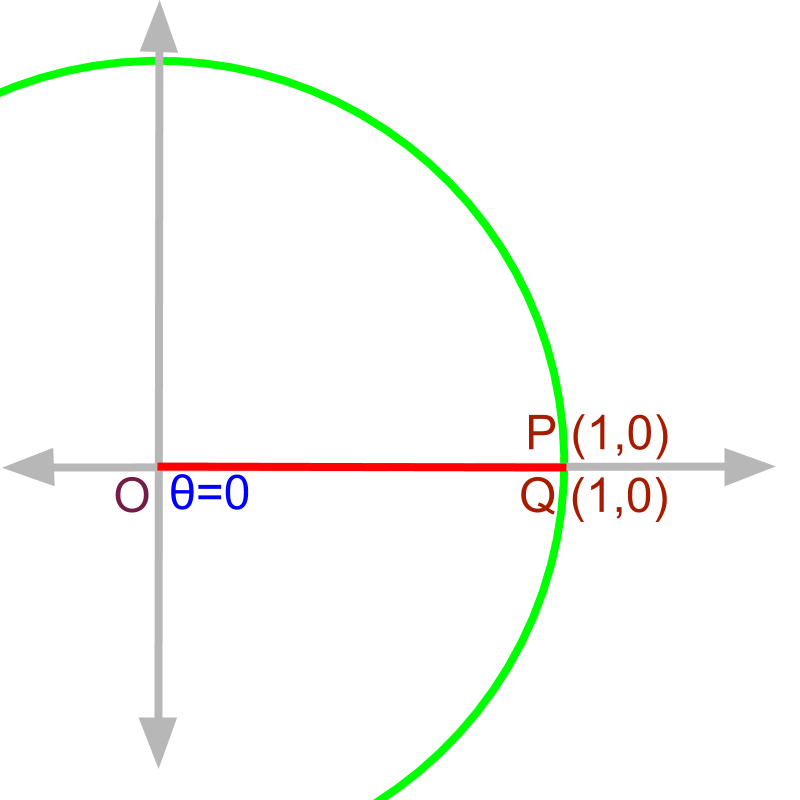
Given the right angled triangle $Δ O P Q$ $Delta OPQ$ , and $∠ P O Q = 0^{\circ}$ $/_POQ = 0^@$ .

$\bar{O Q} = \bar{O P} = 1$ $bar(OQ)=bar(OP)= 1$

The point $P$ $P$ is $(1, 0)$ $(1,0)$

It is proven that point $P (1, 0)$ $P (1, 0)$ . That is,

opposite side $\bar{P Q} = 0$ $bar(PQ) = 0$

adjacent side $\bar{O Q} = 1$ $bar(OQ) = 1$

hypotenuse $\bar{O P} = 1$ $bar(OP) = 1$

${\sin 0}^{\circ} = 0$ $sin 0^@ = 0$

${\cos 0}^{\circ} = 1$ $cos 0^@ = 1$

${\tan 0}^{\circ} = 0$ $tan 0^@ = 0$

It might not be intuitive, but it is possible to work out the lengths of the three sides of a triangle of $0^{\circ}$ $0^@$ degree and work out the trigonometric ratios without memorizing them.

For example, ${\sec 0}^{\circ} = 1$ $sec 0^@ = 1$ .

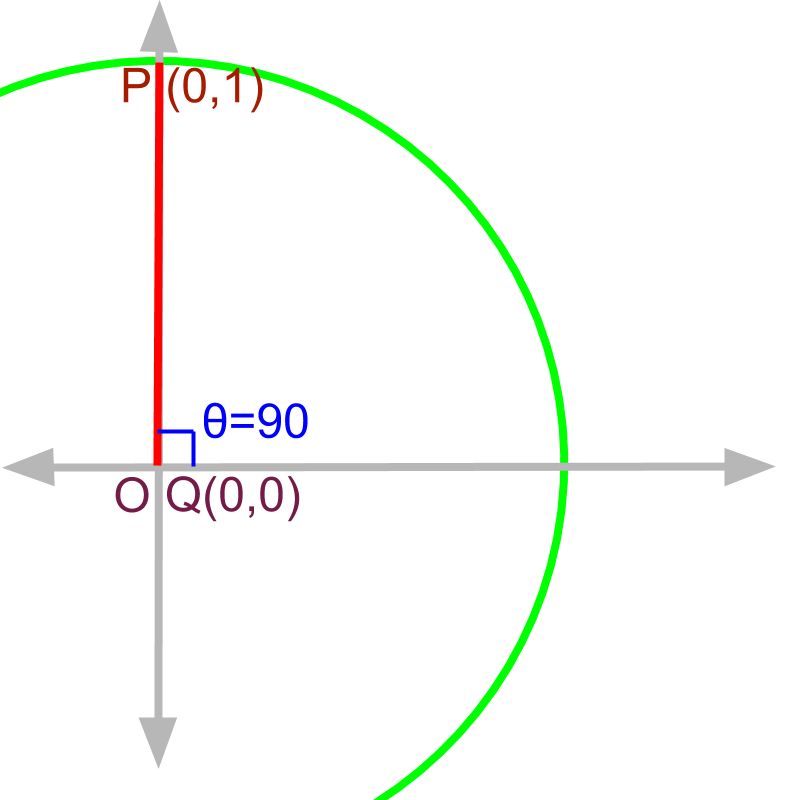
Given the right angled triangle $Δ O P Q$ $Delta OPQ$ , and $∠ P O Q = 90^{\circ}$ $/_POQ = 90^@$ .

$\bar{O P} = \bar{Q P} = 1$ $bar(OP) = bar(QP) = 1$

The point $P$ $P$ is $(0, 1)$ $(0,1)$ .

It is proven that point $P (0, 1)$ $P (0,1)$ . That is,

opposite side $\bar{P Q} = 1$ $bar(PQ) = 1$

adjacent side $\bar{O Q} = 0$ $bar(OQ) = 0$

hypotenuse $\bar{O P} = 1$ $bar(OP) = 1$

${\sin 90}^{\circ} = 1$ $sin 90^@ = 1$

${\cos 90}^{\circ} = 0$ $cos 90^@ = 0$

${\tan 90}^{\circ} = \frac{1}{0}$ $tan 90^@ = 1/0$

Another triangle that is not very intuitive, but it is possible to work out the lengths of the three sides of a triangle of $90^{\circ}$ $90^@$ and work out the trigonometric ratios without memorizing them.

For example, $cosec 90^{\circ} = 1$ $text(cosec) 90^@ = 1$ .

Summary

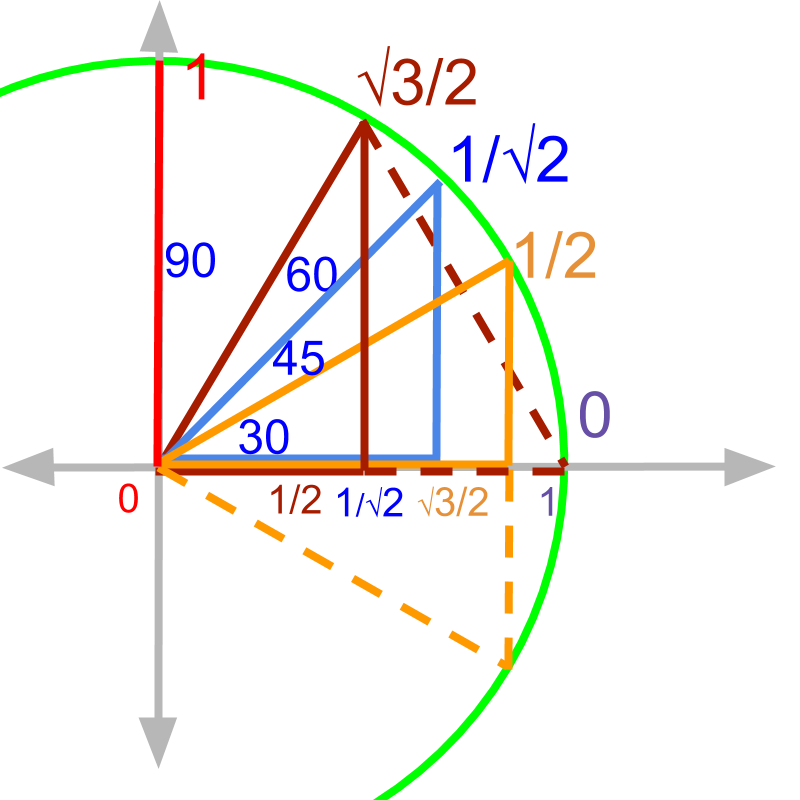
Trigonometric ratios for all standard angles is captured in the figure.

When a trigonometric ratio is required for an angle, quickly work out the $x, y$ $x,y$ for the angle. And sine is chord, cosine is the chord on the complementary angle, tan is the tangent etc. With a little bit of practice, this becomes fast and easy. I hope you do not memorize a table which you will eventually forget. If you can work out from the first principles, the information will last a lot longer. With a little bit of practice, students can recall the ratios as fast as when memorized.

Trigonometric Ratios of Standard Angles:

When a trigonometric ratio is required for an angle, quickly work out the $x, y$ $x,y$ for the angle.

Outline

The outline of material to learn "Basics of Trigonometry" is as follows.

• Detailed outline of "trigonometry".

→ Basics - Angles

→ Basics - Triangles

→ Importance of Right Angled Triangle

→ Trigonometric Ratio (Basics)

→ Triangular Form of Trigonometric Ratios

→ Introduction to Standard Angles

→ Trigonometric Ratio of Standard Angles

→ Trigonometric Identities

→ Trigonometric Ratios of Complementary Angles