Trigonometry (Introduction) : Pythagorean Trigonometric Identities

maths > trigonometry

Pythagorean Trigonometric Identities

what you'll learn...

Overview

» ${opposite}^{2}$ $text(opposite)^2$ $+ {adjacent}^{2}$ $+text(adjacent)^2$ $= {hypotenuse}^{2}$ $= text(hypotenuse)^2$

» Divide the above by ${hypotenuse}^{2}$ $text(hypotenuse)^2$
$\sin^{2} θ + \cos^{2} θ = 1$ $sin^2 theta + cos^2 theta = 1$

» Divide the identity by $\cos^{2} θ$ $cos^2 theta$
$\tan^{2} θ + 1 = \sec^{2} θ$ $tan^2 theta + 1 = sec^2 theta$

» Divide the identiry by $\sin^{2} θ$ $sin^2 theta$
$1 + \cos^{2} θ = \csc^{2} θ$ $1 + cos^2 theta = csc^2 theta$

Identity Proof

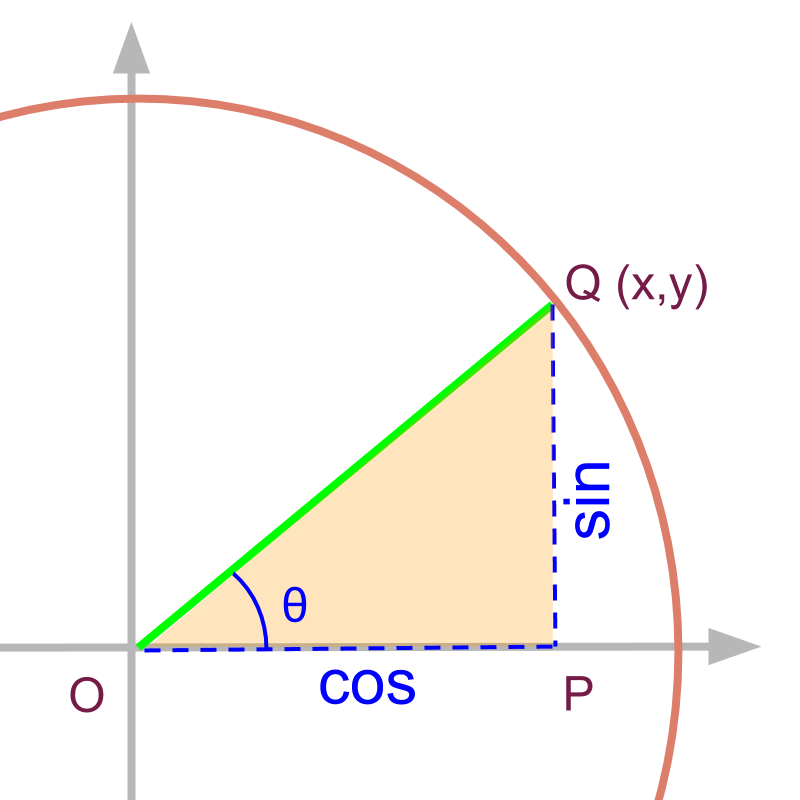
Pythagorean Trigonometric Identities illustration

For the triangle given in figure, $\sin θ = \frac{P Q}{O Q}$ $sin theta = (PQ)/(OQ)$

For the triangle given in figure, $\cos θ = \frac{O P}{O Q}$ $cos theta = (OP)/(OQ)$

The Pythagoras theorem is given as

$O P^{2} + P Q^{2} = O Q^{2}$ $OP^2 + PQ^2 =OQ^2$

Or equivalently

${(\frac{O P}{O Q})}^{2} + {(\frac{P Q}{O Q})}^{2} = 1$ $((OP)/(OQ))^2 + ((PQ)/(OQ))^2 = 1$

For a right angled triangle, the Pythagoras theorem is given as

${(opposite)}^{2}$ $(text(opposite))^2$ $+ {(adjacent)}^{2}$ $+ (text(adjacent))^2$ $= {(hypotenuse)}^{2}$ $= (text(hypotenuse))^2$
$O P^{2} + P Q^{2} = O Q^{2}$ $OP^2 + PQ^2 =OQ^2$

If this equation is divided by ${(hypotenuse)}^{2}$ $(text(hypotenuse))^2$ or $O Q^{2}$ $OQ^2$
${(\frac{O P}{O Q})}^{2} + {(\frac{P Q}{O Q})}^{2} = 1$ $((OP)/(OQ))^2 + ((PQ)/(OQ))^2 = 1$

Or equivalently

$\sin^{2} θ + \cos^{2} θ = 1$ $sin^2 theta + cos^2 theta = 1$

Pythagorean Theorem states that in a right angled triangle, square of hypotenuse equals sum of squares of two arms. The trigonometric ratios are defined for right angled triangles. The relationships between trigonometric ratios per Pythagorean theorem are called "Pythagorean Trigonometric Identities".

$\sin^{2} θ + \cos^{2} θ = 1$ $sin^2 theta + cos^2 theta = 1$

It is noted that the result is true for any value of $θ$ $theta$ . That is, if $θ = 27$ $theta = 27$ , then $\sin^{2} 27^{\circ} + \cos^{2} 27^{\circ} = 1$ $sin^2 27^@ + cos^2 27^@ = 1$

The word "identity" means equality of two expressions; left and right hand sides are identical.

In the Pythagorean Trigonometric Identity $\sin^{2} θ + \cos^{2} θ = 1$ $sin^2 theta + cos^2 theta = 1$ , it is stated that left hand side $\sin^{2} θ + \cos^{2} θ$ $sin^2 theta + cos^2 theta$ equals the right hand side $1$ $1$ .

another identity

For a right angled triangle,

$\sin^{2} θ + \cos^{2} θ = 1$ $sin^2 theta + cos^2 theta = 1$

If this equation is divided by $\sin^{2} θ$ $sin^2 theta$ , the following identity is derived

$1 + \cot^{2} θ = \csc^{2} θ$ $1+cot^2 theta = csc^2 theta$

$1 + \cot^{2} θ = \csc^{2} θ$ $1+cot^2 theta = csc^2 theta$

yet another identity

For a right angled triangle,

$\sin^{2} θ + \cos^{2} θ = 1$ $sin^2 theta + cos^2 theta = 1$

If this equation is divided by $\cos^{2} θ$ $cos^2 theta$ , the following identity is derived.

$\tan^{2} θ + 1 = \sec^{2} θ$ $tan^2 theta + 1 = sec^2 theta$

$\tan^{2} θ + 1 = \sec^{2} θ$ $tan^2 theta + 1 = sec^2 theta$

examples

What is the value of $1 - \sin^{2} θ$ $1-sin^2 theta$ ?
The answer is ' $\cos^{2} θ$ $cos^2 theta$ '.

This is derived from the Pythagorean trigonometric identity $\sin^{2} θ + \cos^{2} θ = 1$ $sin^2 theta + cos^2 theta = 1$

What is the value of $\sec^{2} θ - 1$ $sec^2 theta - 1$ ?
The answer is ' $\tan^{2} θ$ $tan^2 theta$ '.

This is derived from the Pythagorean trigonometric identity $\tan^{2} θ + 1 = \sec^{2} θ$ $tan^2 theta + 1 = sec^2 theta$

What is the value of $\csc^{2} θ - \cot^{2} θ$ $csc^2 theta-cot^2 theta$ ?
The answer is ' $1$ $1$ '.

This is derived from the Pythagorean trigonometric identity $1 + \cot^{2} θ = \csc^{2} θ$ $1 + cot^2 theta = csc^2 theta$

Summary

Pythagorean Trigonometric Identities:

For any theta,

$\sin^{2} θ + \cos^{2} θ = 1$ $sin^2 theta + cos^2 theta = 1$

$1 + \cot^{2} θ = \csc^{2} θ$ $1+cot^2 theta = csc^2 theta$

$\tan^{2} θ + 1 = \sec^{2} θ$ $tan^2 theta + 1 = sec^2 theta$

Note that this need not me memorized, connect these to the Pythogoras theorem and quickly derive when required.

Outline

The outline of material to learn "Basics of Trigonometry" is as follows.

• Detailed outline of "trigonometry".

→ Basics - Angles

→ Basics - Triangles

→ Importance of Right Angled Triangle

→ Trigonometric Ratio (Basics)

→ Triangular Form of Trigonometric Ratios

→ Introduction to Standard Angles

→ Trigonometric Ratio of Standard Angles

→ Trigonometric Identities

→ Trigonometric Ratios of Complementary Angles