Trigonometry (Introduction) : Triangular Form of Trigonometric Ratios

maths > trigonometry

Triangular Form of Trigonometric Ratios

what you'll learn...

Overview

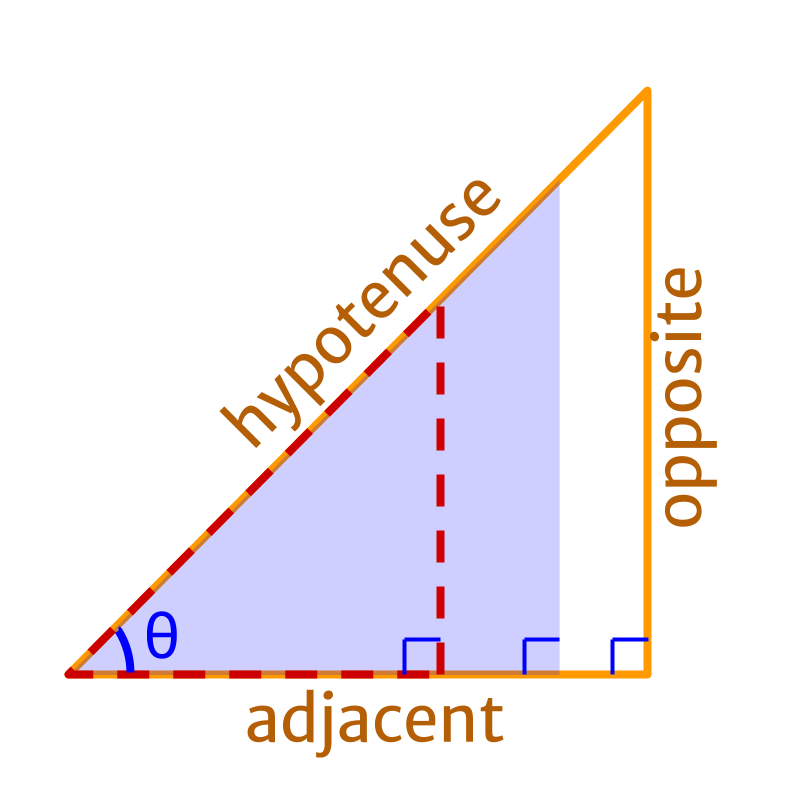
» similar right-triangle

    → given angle $θ$ $theta$

    → position of right-angle with reference to given angle

    → hypotenuse with reference to the right-angle

    → position of a side with reference to the given angle : opposite-side

    → position of another side with reference to the given angle : adjacent-side

» Trigonometric Ratios
    → $\sin θ = \frac{opposite}{hypotenuse}$ $sin theta = text(opposite)/text(hypotenuse)$
    → $\cos θ = \frac{adjacent}{hypotenuse}$ $cos theta = text(adjacent)/text(hypotenuse)$
    → $\tan θ = \frac{opposite}{adjacent}$ $tan theta = text(opposite)/text(adjacent)$ $= \frac{\sin θ}{\cos θ}$ $quad = (sin theta)/(cos theta)$

Note: In advanced trigonometry, a general form "trigonometric values on unit circle" will be introduced.

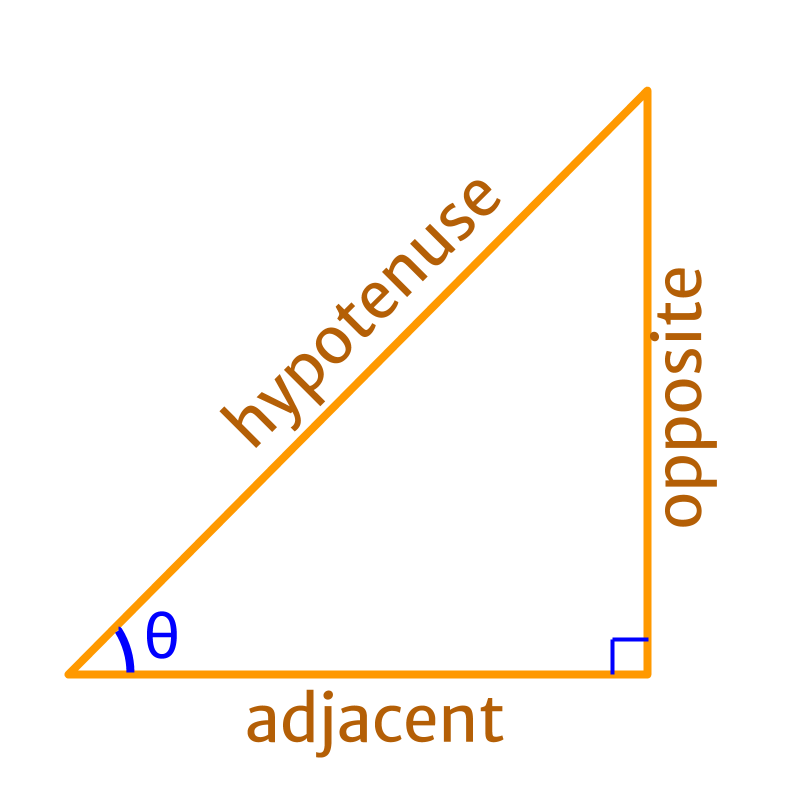
hypotenuse, opposite side, adjacent side

Let us quickly review the terminology in trigonometric ratios.

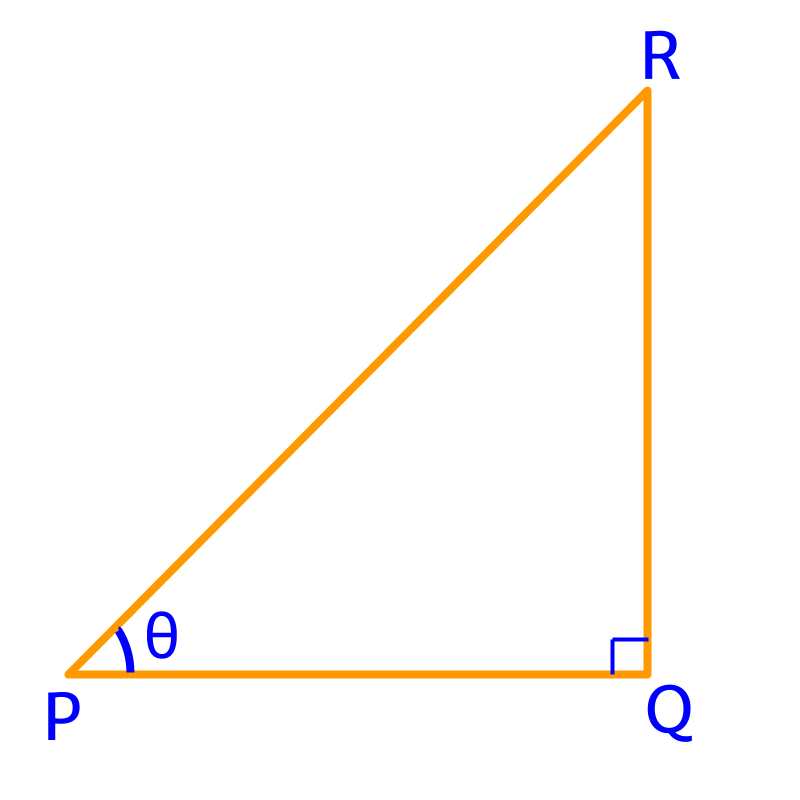
trigonometric ratios triangular form hypotenuse

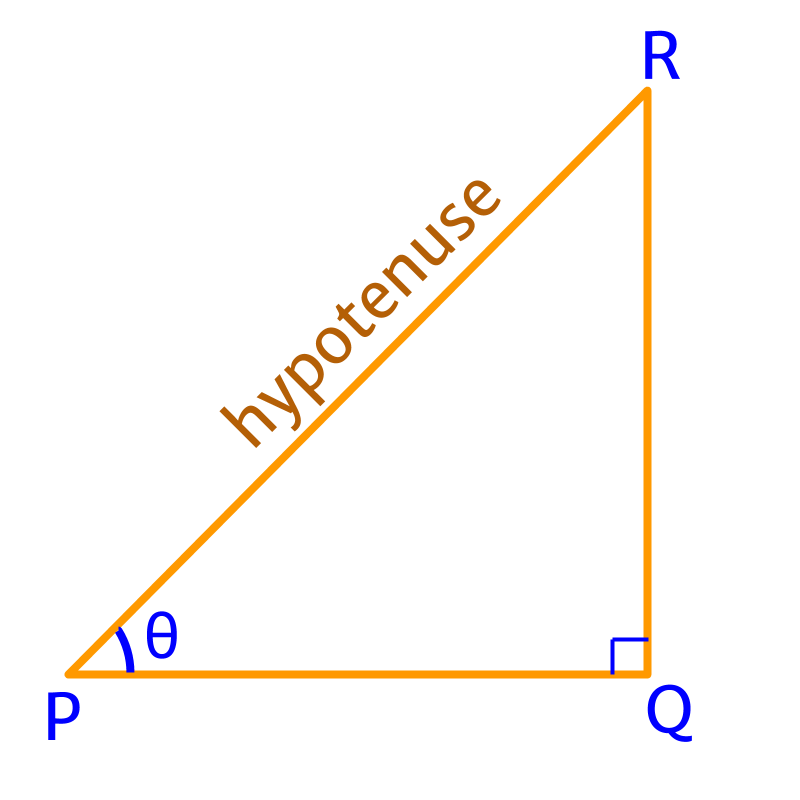
In the given figure, $\bar{P R}$ $bar(PR)$ is the hypotenuse.

trigonometric ratios triangular form opposite side

In the given figure, $\bar{Q R}$ $bar(QR)$ is the opposite side.

In the given figure, $\bar{P Q}$ $bar(PQ)$ is the adjacent side.

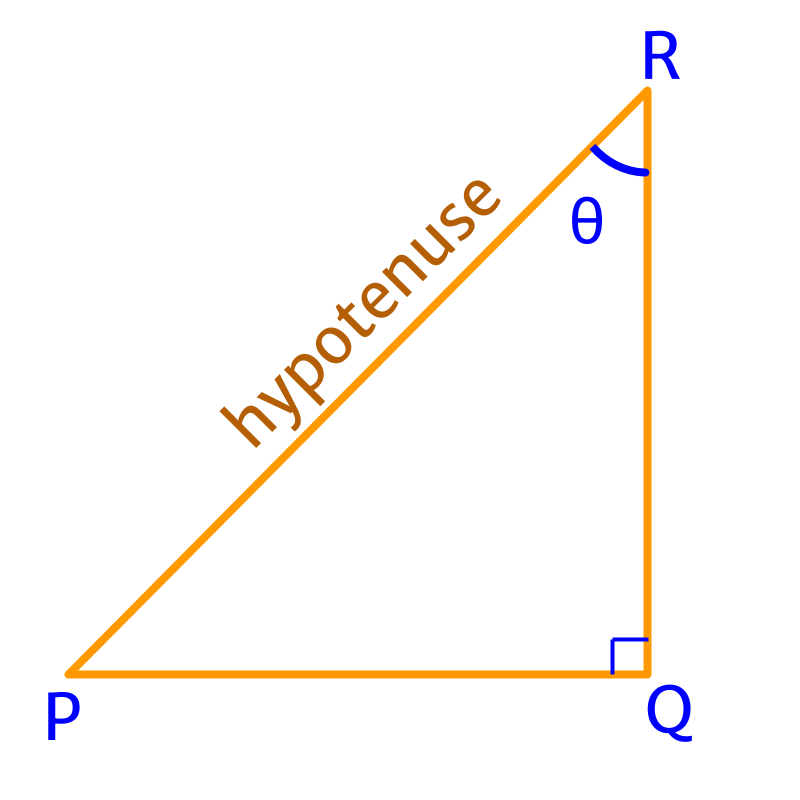
In the given figure, the opposite side to $∠ θ$ $/_theta$ is $\bar{P Q}$ $bar(PQ)$ .

In the given figure, the adjacent side to $∠ θ$ $/_theta$ is $\bar{Q R}$ $bar(QR)$ .

In the given figure, the hypotenuse is $\bar{A B}$ $bar(AB)$ .

In the given figure, the hypotenuse is $\bar{A C}$ $bar(AC)$ .

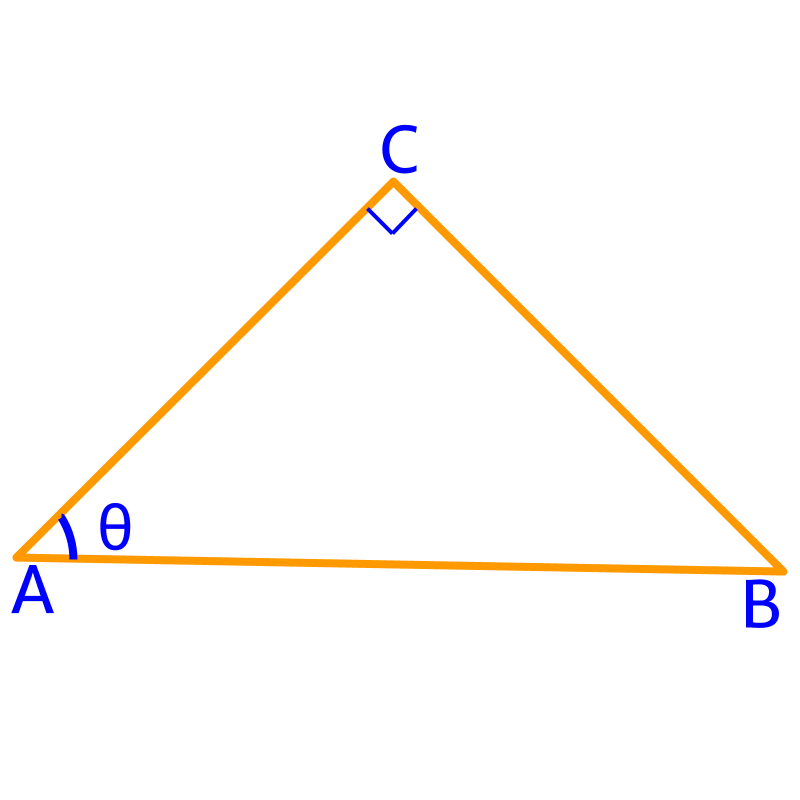
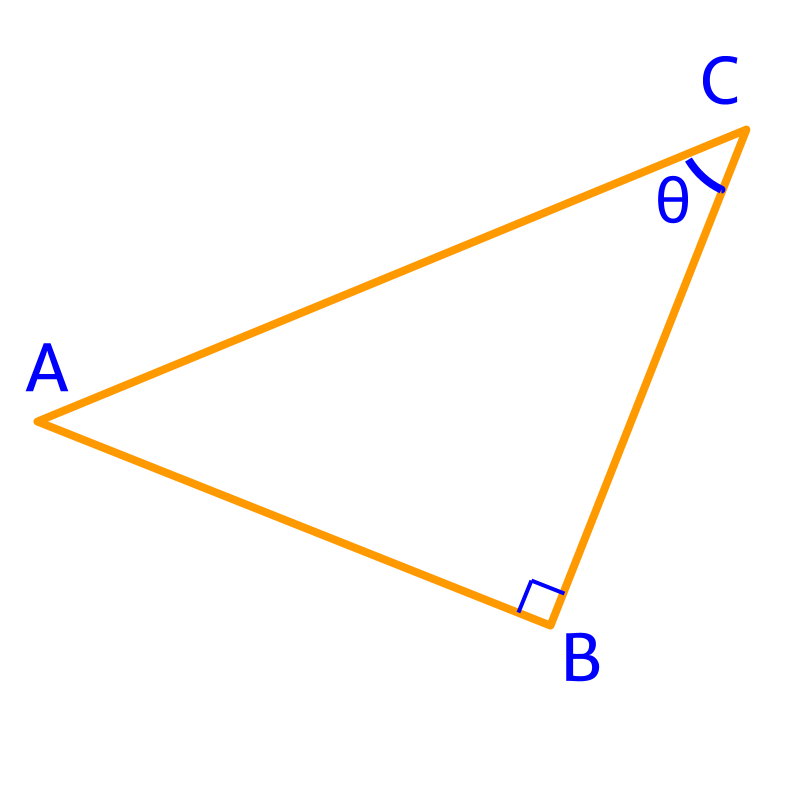
In the given figure, the opposite side to $∠ θ$ $/_theta$ is $\bar{B C}$ $bar(BC)$ .

trigonometric ratios triangular form adjacent side

In the given figure, the adjacent side to $∠ θ$ $/_theta$ is $\bar{B C}$ $bar(BC)$ .

sin, cos, tan

$\sin θ = \frac{opposite}{hypotenuse}$ $sin theta = text(opposite)/text(hypotenuse)$

$\cos θ = \frac{adjacent}{hypotenuse}$ $cos theta = text(adjacent)/text(hypotenuse)$

$\tan θ = \frac{opposite}{adjacent}$ $tan theta = text(opposite)/text(adjacent)$

$\tan θ = \frac{\sin θ}{\cos θ}$ $tan theta = (sin theta)/(cos theta)$

sec, cosec, cot

$\frac{1}{\cos θ} = \frac{hypotenuse}{adjacent}$ $1/(cos theta) = text(hypotenuse)/text(adjacent)$

$\frac{1}{\cos θ}$ $1/(cos theta)$ is called as ' $\sec θ$ $sec theta$ '

$\sec θ$ $sec theta$

$= \frac{hypotenuse}{adjacent}$ $quad quad = text(hypotenuse)/text(adjacent)$

$= \frac{1}{\cos θ}$ $quad quad = 1/ (cos theta)$

$\frac{1}{\sin θ} = \frac{hypotenuse}{opposite}$ $1/(sin theta) = text(hypotenuse)/text(opposite)$

$\frac{1}{\sin θ}$ $1/(sin theta)$ is called as ' $cosec θ$ $text(cosec) theta$ ' or ' $\csc θ$ $csc theta$ '

$cosec θ$ $text(cosec) theta$ or $\csc θ$ $csc theta$

$= \frac{hypotenuse}{opposite}$ $quad quad = text(hypotenuse)/text(opposite)$

$= \frac{1}{\sin θ}$ $quad quad = 1/ (sin theta)$

$\frac{1}{\tan θ} = \frac{adjacent}{opposite}$ $1/(tan theta) = text(adjacent)/text(opposite)$

$\frac{1}{\tan θ}$ $1/(tan theta)$ is called as ' $\cot θ$ $cot theta$ '.

$cot θ$ $text(cot) theta$

$= \frac{adjacent}{opposite}$ $quad quad = text(adjacent)/text(opposite)$

$= \frac{1}{\tan θ}$ $quad quad = 1/ (tan theta)$

Summary

Trigonometric Ratios:
$\sin θ = \frac{opposite}{hypotenuse}$ $sin theta = text(opposite)/text(hypotenuse)$

$\cos θ = \frac{adjacent}{hypotenuse}$ $cos theta = text(adjacent)/text(hypotenuse)$

$\tan θ = \frac{opposite}{adjacent}$ $tan theta = text(opposite)/text(adjacent)$

$\sec θ = \frac{hypotenuse}{adjacent}$ $sec theta = text(hypotenuse)/text(adjacent)$

$cosec θ = \frac{hypotenuse}{opposite}$ $text(cosec) theta = text(hypotenuse)/text(opposite)$

$\cot θ = \frac{adjacent}{opposite}$ $cot theta = text(adjacent)/text(opposite)$

Outline

The outline of material to learn "Basics of Trigonometry" is as follows.

• Detailed outline of "trigonometry".

→ Basics - Angles

→ Basics - Triangles

→ Importance of Right Angled Triangle

→ Trigonometric Ratio (Basics)

→ Triangular Form of Trigonometric Ratios

→ Introduction to Standard Angles

→ Trigonometric Ratio of Standard Angles

→ Trigonometric Identities

→ Trigonometric Ratios of Complementary Angles