Trigonometry (Introduction) : Basics of Angles

maths > trigonometry

Basics of Angles

what you'll learn...

Overview

» Angle is measured in degree or radian

» Right Angle : $90^{\circ}$ $90^@$

» Complementary Angles : pair of angles with sum $90^{\circ}$ $90^@$

» Straight Angle : $180^{\circ}$ $180^@$

» Supplementary Angles : pair of angles with sum $180^{\circ}$ $180^@$

Angle

Before starting with Trigonometry, let us revise the basics required to understand that.

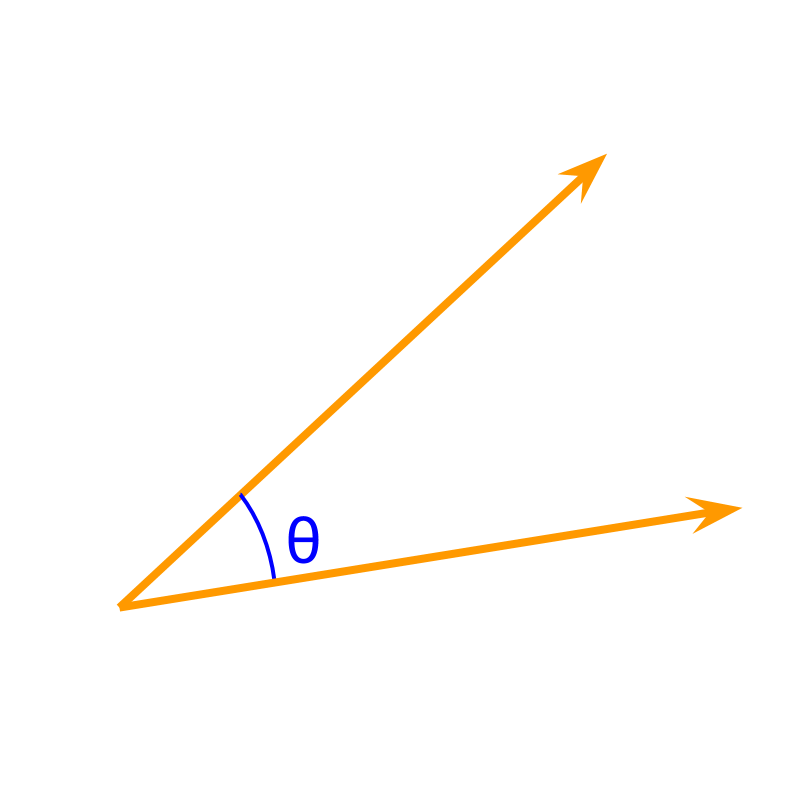
An angle is the measure of rotation between two lines.

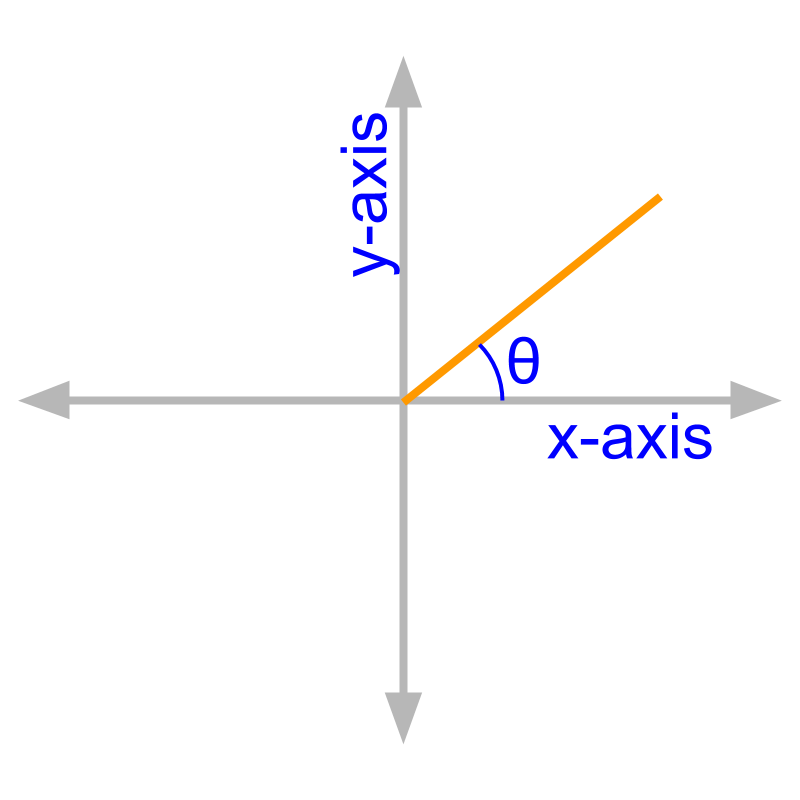
An angle for a given line in a coordinate system is, the angle from the x-axis to the line, measured in anti-clockwise direction.

Degree and Radian

An angle is measured in degree or radian.

The measure of angle, "degree" is defined by -- Rotation by a full circle is graded into $360$ $360$ degrees.

From the figure, one should understand.

• The angles are measured with respect to the +ve x-axis.

• The graded angles are represented for $20^{\circ}, 40^{\circ}, 60^{\circ}, \dots$ $20^@, 40^@, 60^@, cdots$ .

• A line making an angle $30^{\circ}$ $30^@$ is shown.

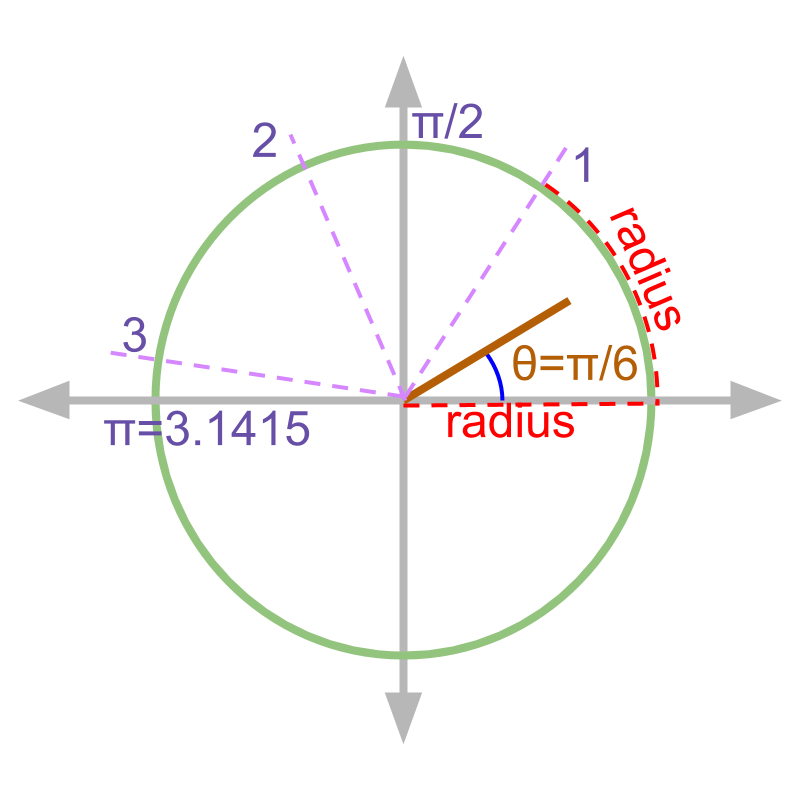
The measure of angle, "radian" is defined by -- $1$ $1$ radian = angle subtended in a circle, by the arc of length equaling the radius.

From the figure, one should understand

• radius of the circle is shown in red dotted line. An arc having length equal to radius of the circle is shown in red dotted arc.

• The radian measures $1, 2, 3$ $1, 2, 3$ radians are marked

• The y-axis at $90^{\circ}$ $90^@$ angle is at $\frac{π}{2}$ $pi/2$ radian.

• the -ve x-axis at $180^{\circ}$ $180^@$ angle is at $π$ $pi$ radian.

• the full-circle subtends $2 π$ $2pi$ radian or $360^{\circ}$ $360^@$ angle.

• line making $30^{\circ}$ $30^@$ angle is shown and the angle in radians is $\frac{π}{6}$ $pi/6$ .

Positive and Negative Angles

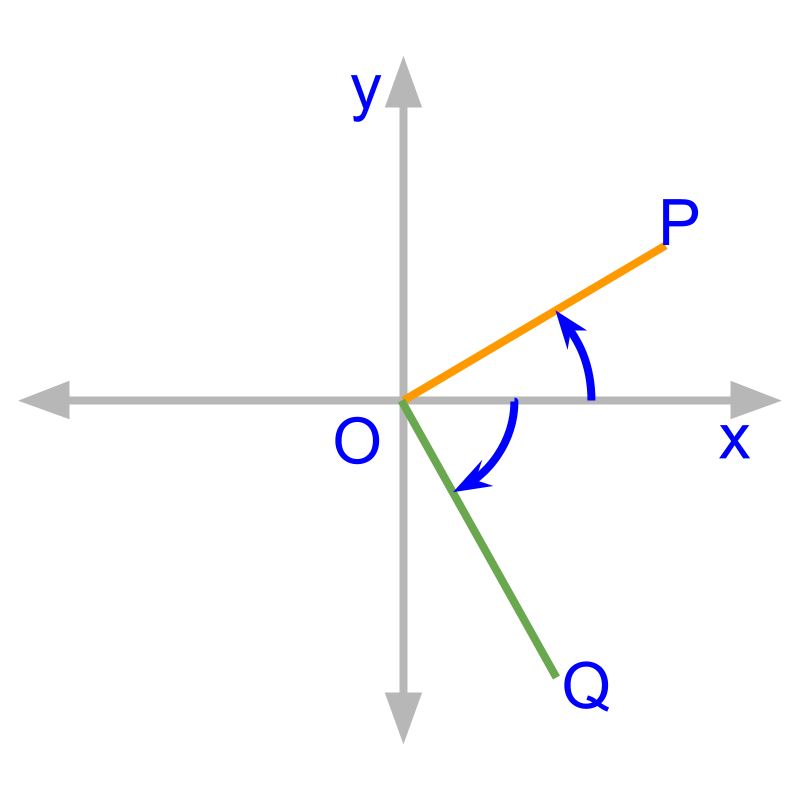
An angle is positive if it is measured in counter-clockwise direction.

The figure shows $+ 30^{\circ}$ $+30^@$

An angle is negative if it is measured in clockwise direction.

The figure shows $- 60^{\circ}$ $-60^@$

The measure of angle $∠ P Q R$ $/_PQR$ is $- 30^{\circ}$ $-30^@$ .

The angle is measured from $\bar{P Q}$ $bar(PQ)$ to $\bar{Q R}$ $bar(QR)$ , in clockwise direction.

Some Standard Angles

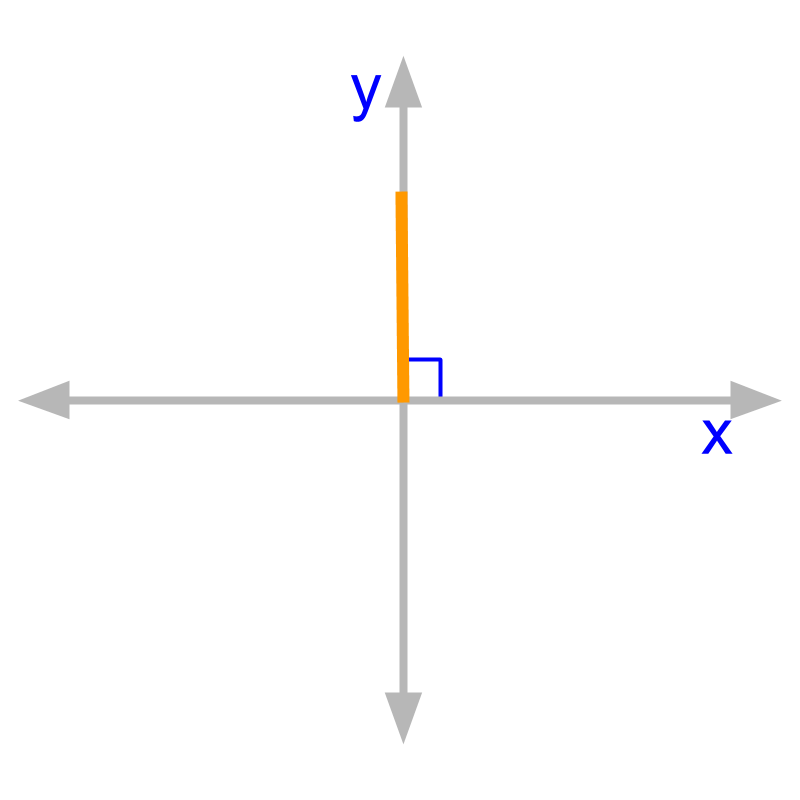
Right angle is angle of measure $90^{\circ}$ $90^@$ or $\frac{π}{2}$ $pi/2$ radian. Note $90^{\circ} = \frac{π}{2}$ $90^@ = pi/2$ radian

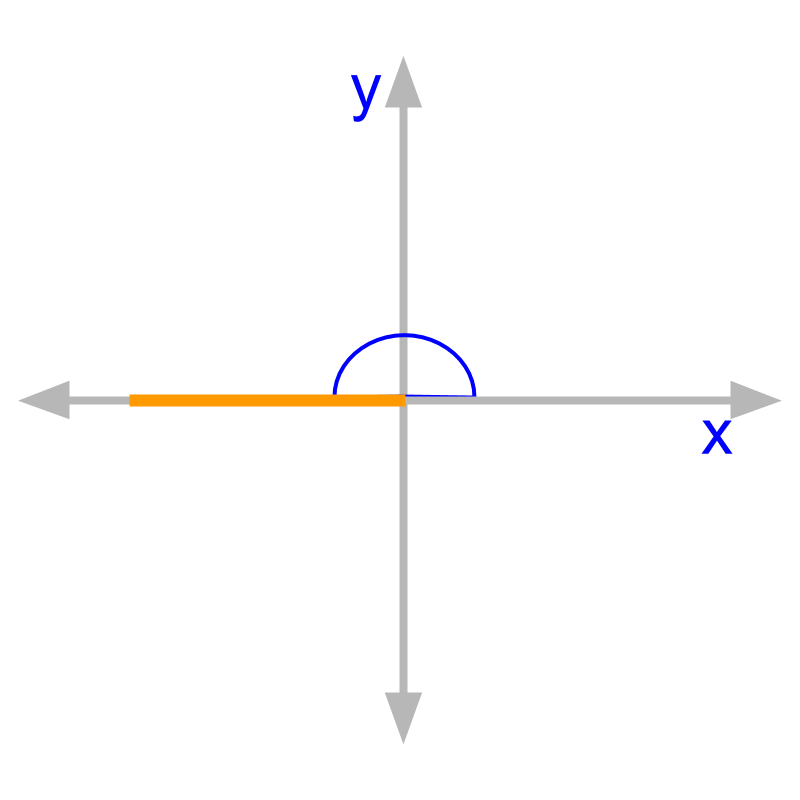
Straight angle is angle of measure $180^{\circ}$ $180^@$ or $π$ $pi$ radian.

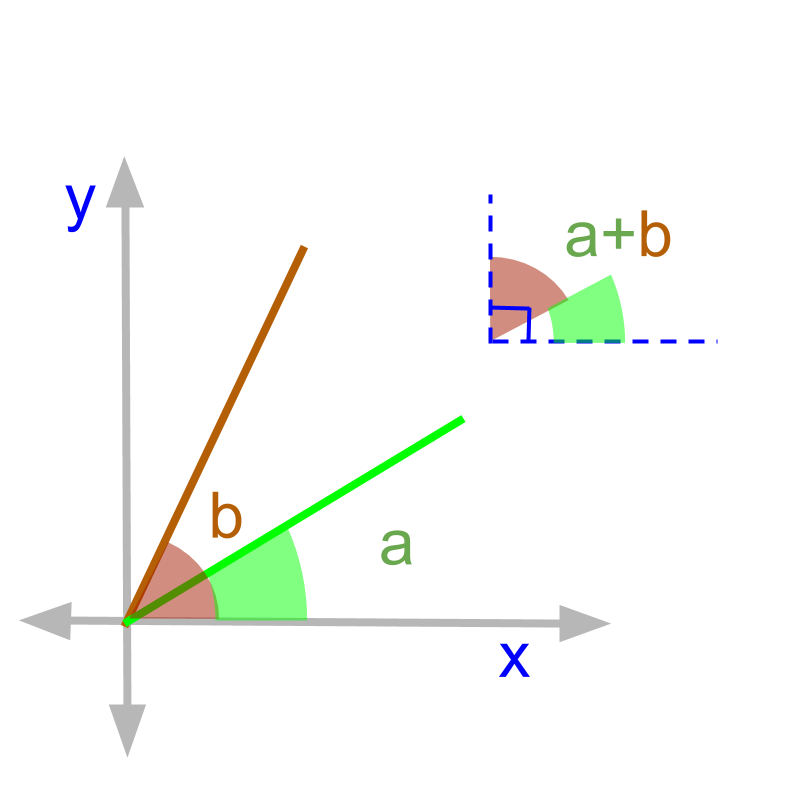
Pair of angles having sum $90^{\circ}$ $90^@$ are called complementary angles.

The word "complementary" is derived from the word "complete". When one angle completes the right angle with another angle, the angles are called complementary angles.

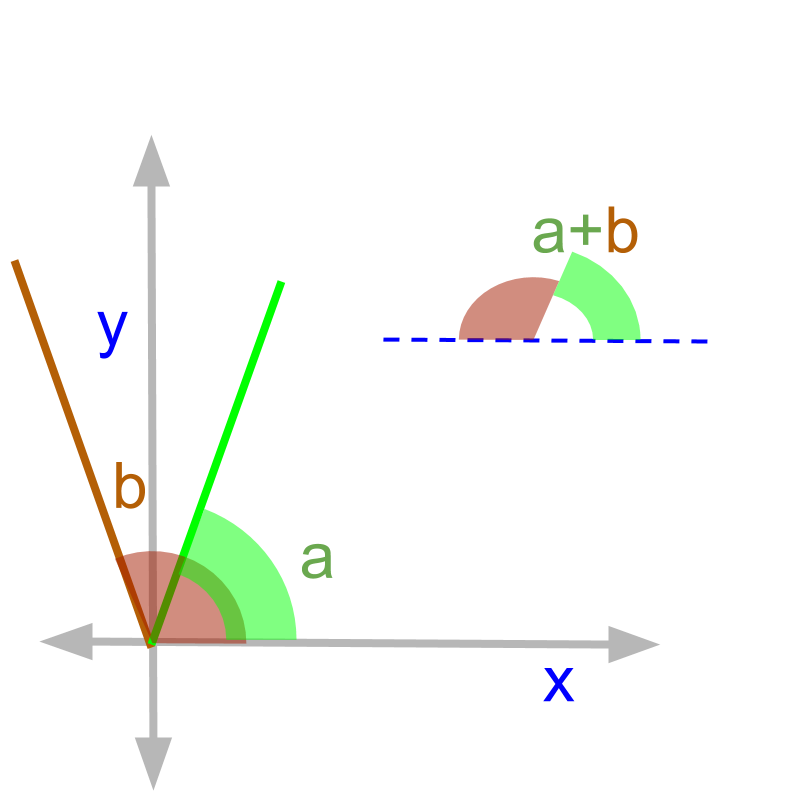
Pair of angles having sum $180^{\circ}$ $180^@$ are called Supplementary Angles.

The word "supplement" means "comes as an addition".
In a straight line the pair of supplementary angles come together.

The two angles $52^{\circ}$ $52^@$ and $38^{\circ}$ $38^@$ are complementary angles.

The two angles $92^{\circ}$ $92^@$ and $88^{\circ}$ $88^@$ are supplementary angles.

Summary

Basics of Angles to learn trigonometry :

• Angles are measured in degrees and radians.

• Right angle and Straight Angle.

• Complementary and Supplementary angles.

Angle: For two line segments or rays with common initial point, the amount of rotation in counter clockwise direction from one to another is the angle.

Degree: Rotation by a full circle is graded as $360^{\circ}$ $360^@$ and angles are measured in that graded scale.

Radian: Rotation by the length of radius along the arc of a circle, is $1$ $1$ radian. Angles are measured in proportion to the $1$ $1$ radian measure.

Right Angle: Angle of $90^{\circ}$ $90^@$ or $\frac{π}{2}$ $pi/2$ radian.

Straight Angle: Angle of $180^{\circ}$ $180^@$ or $π$ $pi$ radian.

Complementary Angles: Pair of angles having sum $90^{\circ}$ $90^@$ .

Supplementary Angles: Pair of angles having sum $180^{\circ}$ $180^@$ .

Outline

The outline of material to learn "Basics of Trigonometry" is as follows.

• Detailed outline of "trigonometry".

→ Basics - Angles

→ Basics - Triangles

→ Importance of Right Angled Triangle

→ Trigonometric Ratio (Basics)

→ Triangular Form of Trigonometric Ratios

→ Introduction to Standard Angles

→ Trigonometric Ratio of Standard Angles

→ Trigonometric Identities

→ Trigonometric Ratios of Complementary Angles