Fractions : Equivalent Fractions and Simplest form of a fraction

maths > fractions

Equivalent Fractions and Simplest form of a fraction

what you'll learn...

overview

In this page, equivalent fractions and simplest form of a fraction are explained

• Two or more fractions that specify the same amount with different place values are equivalent fractions.

• Among the set of equivalent fractions, the fraction with lowest denominator (representing lowest number of cuts of the whole) is the simplest form of a fraction.

split into more or less

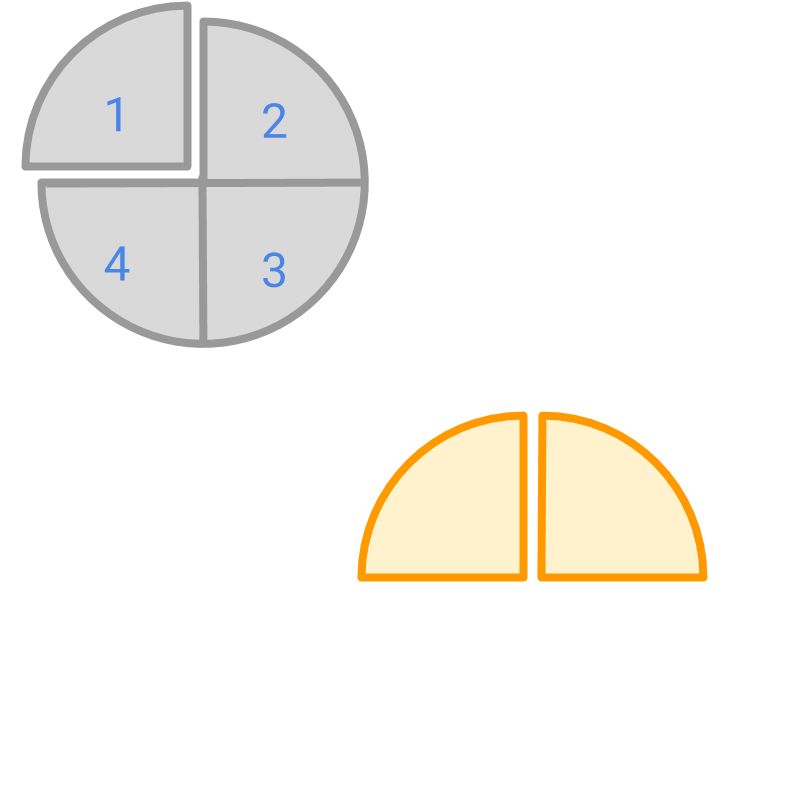
$equivalent fraction 2/4$

The whole is split into $4$ $4$ pieces and $2$ $2$ pieces are considered. The fraction represented by the colored part is $\frac{2}{4}$ $2/4$

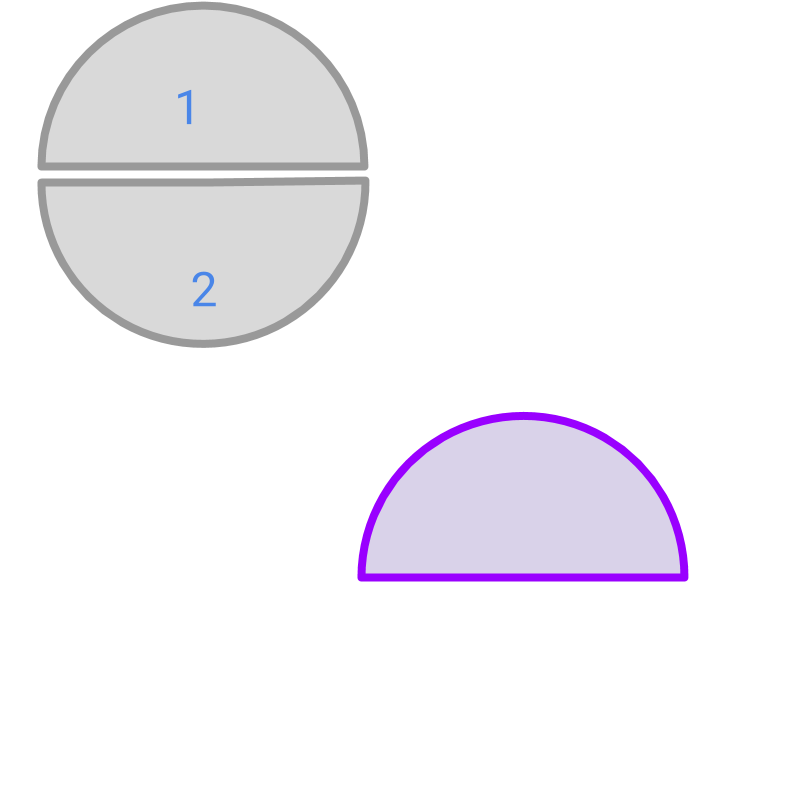
$equivalent fraction 1/2$

Whole is split into $2$ $2$ pieces and $1$ $1$ piece is considered. The fraction represented by the colored portion is $\frac{1}{2}$ $1/2$ .

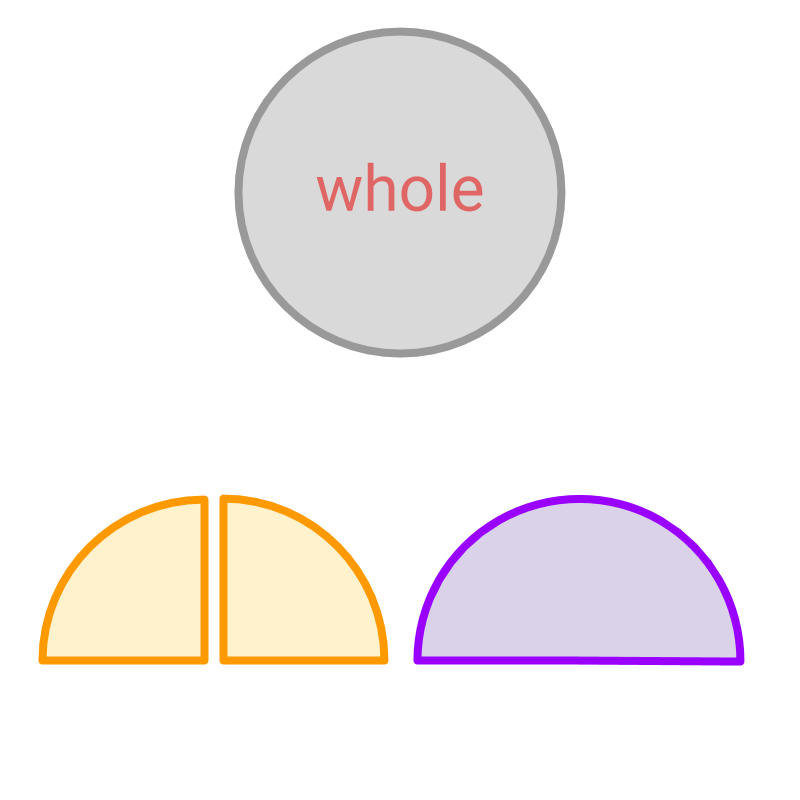
$equivalent fraction 2 by 4 and 1/2$

The picture shows three parts in three different colors.

• The gray part shows the whole

• The orange part shows the fraction $\frac{2}{4}$ $2/4$

• The purple part shows the fraction $\frac{1}{2}$ $1/2$

The fraction $\frac{2}{4}$ $2/4$ and $\frac{1}{2}$ $1/2$ represent the same amount and the same number.

The numerator and denominator of one fraction is a multiple of numerator and denominator of another fraction respectively. Such fractions are called equivalent fractions.

The word "equivalent" means equal in value or amount. The equivalent fractions are fraction of equal amount.

simplify

$simplest form of fractions$

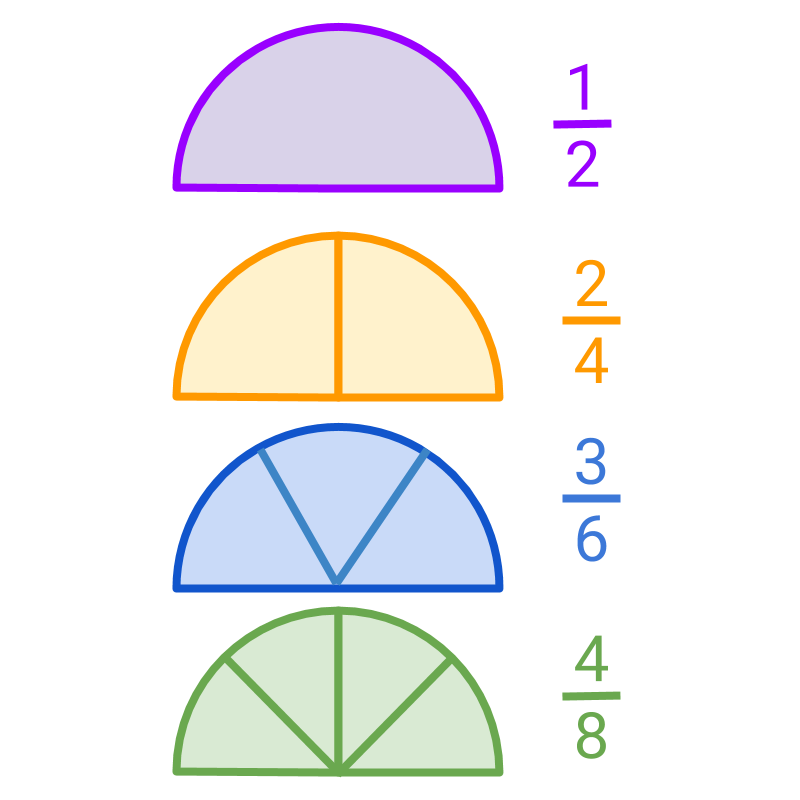
The picture shows four fractions , $\frac{1}{2}$ $1/2$ , $\frac{2}{4}$ $2/4$ , $\frac{3}{6}$ $3/6$ , and $\frac{4}{8}$ $4/8$ . These are equivalent fractions.

The fractions $\frac{2}{4}$ $2/4$ , $\frac{3}{6}$ $3/6$ , and $\frac{4}{8}$ $4/8$ have numerator and denominator with common factors $2$ $2$ , $3$ $3$ and $4$ $4$ respectively.

It is noted that
• in $\frac{1}{2}$ $1/2$ , the whole is cut into two pieces,
• in $\frac{2}{4}$ $2/4$ the whole is cut into four pieces,
• And so on for $\frac{3}{6}$ $3/6$ and $\frac{4}{8}$ $4/8$ , with six and eight pieces respectively.
All these fractions represent the same amount and among these, $\frac{1}{2}$ $1/2$ has the smallest number of cuts. It is the simplest form of all fractions.

It is noted that, only the fraction $\frac{1}{2}$ $1/2$ has no common factor between numerator and denominator.
A fraction without a common factor between the numerator and the denominator is the simplest form of the equivalent fractions.

The word "simplest" means: without complexity, plain, simple and elementary. A fraction without a common factor between the numerator and the denominator is the simplest form of the equivalent fractions.

Fractions that specify the same amount with different place values are equivalent fractions.

The fraction that specifies the same amount with lowest denominator possible is the simplest form of equivalent fractions.

Equivalent Fraction: Two fractions $\frac{p}{q}$ $p/q$ and $\frac{l}{m}$ $l/m$ are equivalent if the numerators $l$ $l$ , $p$ $p$ and the denominators $m$ $m$ , $q$ $q$ have a common factor $a$ $a$ .

That is
$l = a \times p$ $quad l = a xx p$ and
$m = a \times q$ $quad m = a xx q$ .
$a$ $a$ is an integer.
Note that, $\frac{l}{m}$ $l/m$ and $\frac{p}{q}$ $p/q$ specify the same amount with different place values.

Simplest Form of a fraction: A fraction $\frac{p}{q}$ $p/q$ without a common factor between the numerator and the denominator is the simplest form of the equivalent fractions. That is, $p \neq a \times q$ $p != a xx q$ for any integer $a$ $a$ .

Given fractions $\frac{1}{2}$ $1/2$ and $\frac{2}{4}$ $2/4$ . Which one is the simple form of the given equivalent fractions?
' $\frac{1}{2}$ $1/2$ ' is the simple form of the two fractions. .

summary

» Equivalent Fractions
    → fractions that specify the same amount with different place values
» Simplest Form
    → fraction that specify the amount in lowest denominator possible
    → eg: Simplest form of $\frac{2}{4}$ $2/4$ is $\frac{1}{2}$ $1/2$

Outline

The outline of material to learn "fractions" is as follows.

• click here for detailed outline of Fractions

→ Part of whole

→ Dividing a group

→ Fractions as Directed numbers

→ Like and Unlike Fractions

→ Proper and Improper Fractions

→ Equivalent & Simplest form

→ Converting unlike and like Fractions

→ Simplest form of a Fraction

→ Comparing Fractions

→ Addition & Subtraction

→ Multiplication

→ Reciprocal

→ Division

→ Numerical Expressions with Fractions

→ PEMA / BOMA