Fractions : Addition and Subtraction of Fractions

maths > fractions

Addition and Subtraction of Fractions

what you'll learn...

overview

In this addition and subtraction of fractions is covered with the following.

• adding or subtracting the numerators of like fractions

combine or take away

In whole numbers, we had studied the following.

Addition - First Principles : Two numbers are considered, each of which represents a count or measurement. The quantities represented by the numbers are combined to form a result representing a combined count or measurement. The combined count or measurement is the result of addition.

eg: $20$ $20$ and $13$ $13$ are combined together $20 + 13 = 33$ $20+13 = 33$ .

$20$ $20$ is an addend

$13$ $13$ is also an addend

$33$ $33$ is the sum

Subtraction - First Principles : Two numbers are considered, each of which represents a count or measurement. From one amount represented by the first number, the amount represented by the second is taken away to form a result representing the remaining amount. The count or measurement of the remaining amount is the result of subtraction.

eg: $20 - 13 = 7$ $20-13 = 7$

$20$ $20$ is the minuend

$13$ $13$ is the subtrahend

$7$ $7$ is the difference

combine when alike

There are two fractions represented in the figure in two colors. The sum of these two fractions is not simple addition of $3$ $3$ and $2$ $2$ , as the fractions have different place-values. Let us examine problems of addition of fractions.

$addition like fractions$

Consider two other fractions shown in colored parts. The place value of the two fractions are given. The fractions are $\frac{3}{8}$ $3/8$ and $\frac{2}{8}$ $2/8$ . Since the place values are same, we can add the counts. The combined amount is $5$ $5$ pieces in place value $8$ $8$ . That is fraction $\frac{5}{8}$ $5/8$ .

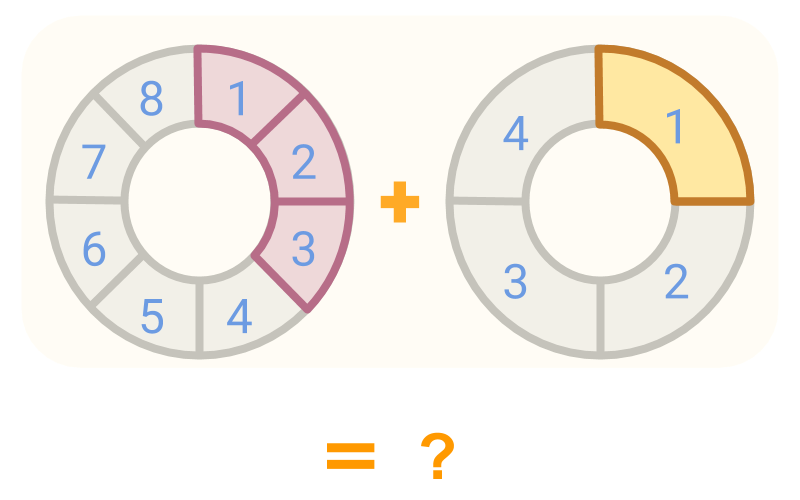
$addition unlike like fractions$

Given two fractions $\frac{1}{4}$ $1/4$ and $\frac{3}{8}$ $3/8$ in the figure. Can these be combined?

The combined quantities is not the sum of the number of pieces, as the $1$ $1$ piece of $\frac{1}{4}$ $1/4$ is double in size of $1$ $1$ piece of $\frac{3}{8}$ $3/8$ . So, it is better to convert the fractions to pieces of same sizes.

$addition unlike like fractions$

Given two fractions $\frac{1}{4}$ $1/4$ and $\frac{3}{8}$ $3/8$ in the figure, the fraction $\frac{1}{4}$ $1/4$ is converted to equivalent fraction $\frac{2}{8}$ $2/8$ .

The place value of the fractions are same, or in other words, the size of the pieces are same.

Now the pieces can be counted. The sum is calculated as $\frac{2}{8} + \frac{3}{8} = \frac{5}{8}$ $2/8 + 3/8 = 5/8$ .

To add the two fractions, the fractions are converted first to like fractions.

take away when alike

$subtraction like fractions$

Consider two other fractions shown in colored parts. The place value of the two fractions are given. The fractions are $\frac{3}{8}$ $3/8$ and $\frac{2}{8}$ $2/8$ .

Subtracting of $\frac{2}{8}$ $2/8$ from $\frac{3}{8}$ $3/8$ : $\frac{3}{8} - \frac{2}{8}$ $3/8-2/8$ . Since the place values or denominators are equal, we can subtract the counts. The remaining amount is $1$ $1$ piece in place value $\frac{1}{8}$ $1/8$ . That is fraction $\frac{1}{8}$ $1/8$ .

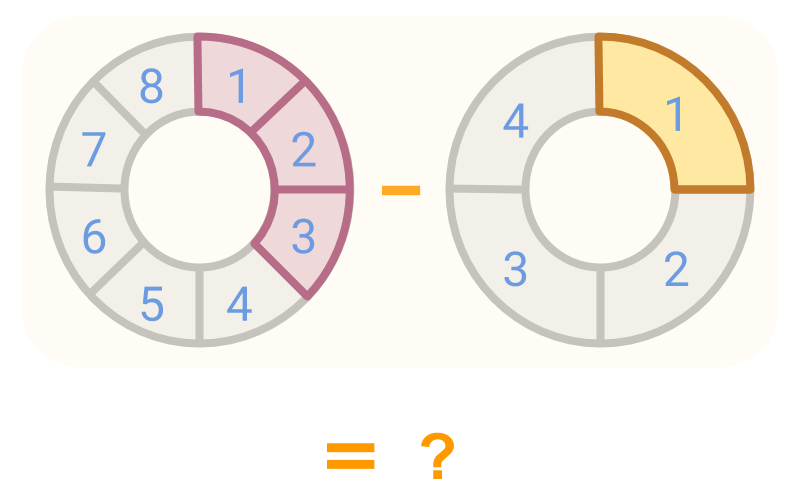
$subtraction unlike like fractions$

Consider the two fractions from the figure, $\frac{3}{8}$ $3/8$ and $\frac{1}{4}$ $1/4$ . Can these be subtracted?

As the $1$ $1$ piece of $\frac{1}{4}$ $1/4$ is double in size of $1$ $1$ piece of $\frac{3}{8}$ $3/8$ , these cannot be subtracted directly. So, the fractions are converted to same place values.

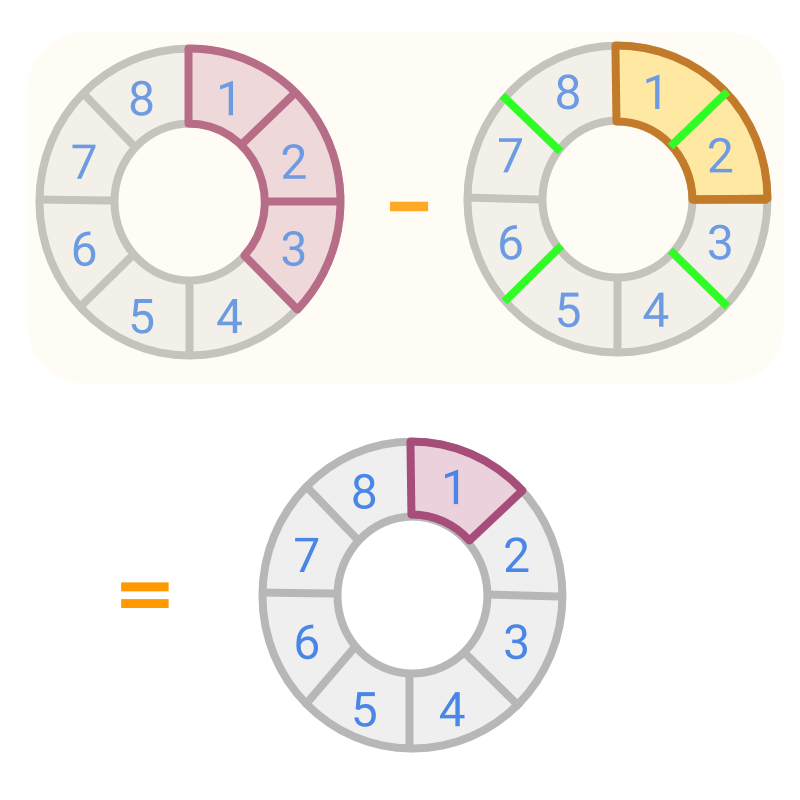
$subtraction unlike like fractions$

Given two fractions $\frac{3}{8}$ $3/8$ and $\frac{1}{4}$ $1/4$ in the figure, the fraction $\frac{1}{4}$ $1/4$ is converted to equivalent fraction $\frac{2}{8}$ $2/8$ . The place values or denominators of the fractions are equal, or in other words, the size of the pieces are same.

Now the pieces can be taken away. The difference is calculated as $\frac{3}{8} - \frac{2}{8} = \frac{1}{8}$ $3/8-2/8 = 1/8$ .

To subtract the two fractions, the fractions are converted first to like fractions.

Convert the fractions to "like fractions" (having same place value) to add or subtract numerators.

add directed numbers

Fractions are directed numbers with positive and negative values.

So far we considered only positive fractions while learning addition and subtraction. Now, let us consider addition and subtraction of positive and negative fractions.

Integer Addition -- First Principles : Directed whole numbers addition is combining the two amounts with direction information taken into account.

Examples are:
• $received: 3$ $text(received:)3$ + $received: 2$ $text(received:)2$ = $received: 5$ $text(received:)5$
$3 + 2 = 5$ $3+2 = 5$

• $received: 3$ $text(received:)3$ + $given: 2$ $text(given:)2$ = $received: 1$ $text(received:)1$
$3 + (- 2) = 3 - 2 = 1$ $3+(−2) = 3−2 = 1$

• $given: 3$ $text(given:)3$ & $received: 2$ $text(received:)2$ = $given: 1$ $text(given:)1$
$- 3 + 2 = - 1$ $-3+2 = -1$

• $received: 3$ $text(received:)3$ & $given: 5$ $text(given:)5$ = $given: 2$ $text(given:)2$
$3 + (- 5) = 3 - 5 = - 2$ $3+(−5) = 3−5 = −2$

• $given: 3$ $text(given:)3$ + $given: 2$ $text(given:)2$ = $given: 5$ $text(given:)5$
$- 3 + (- 2) = - 5$ $−3+(−2) = −5$

adding directed fractions

Adding two fractions $- \frac{1}{4}$ $-1/4$ and $\frac{1}{2}$ $1/2$ .

The fractions are unlike fractions, and so are converted to like fractions first.
$- \frac{1}{4} = given: \frac{1}{4}$ $-1/4 = text(given:)1/4$
$\frac{1}{2} = received: \frac{2}{4}$ $1/2 = text(received:)2/4$

Given 1 count and received 2 counts together is received 1 count.

So, $- \frac{1}{4} + \frac{1}{2} = + \frac{1}{4}$ $-1/4 + 1/2 = + 1/4$

Adding two fractions $\frac{1}{4}$ $1/4$ and $- \frac{1}{2}$ $-1/2$ .

The given fractions are unlike fractions and so are converted to like fractions.

$\frac{1}{4} = received: \frac{1}{4}$ $1/4 = text(received:)1/4$
$- \frac{1}{2} = given: \frac{2}{4}$ $-1/2 = text(given:)2/4$

Received $1$ $1$ count and given $2$ $2$ counts together is given $1$ $1$ count.

So, $\frac{1}{4} + \frac{- 1}{2} = \frac{- 1}{4}$ $1/4 + (-1)/2 = (-1)/4$

Adding two fractions $- \frac{1}{4}$ $-1/4$ and $- \frac{1}{2}$ $-1/2$ .

The like fractions in directed format are
$\frac{- 1}{4} = given: \frac{1}{4}$ $(-1)/4 = text(given:)1/4$
$\frac{- 1}{2} = given: \frac{2}{4}$ $(-1)/2 = text(given:)2/4$

Given $1$ $1$ count and given $2$ $2$ counts together is given $3$ $3$ counts.

So, $- \frac{1}{4} + \frac{- 1}{2} = \frac{- 3}{4}$ $-1/4 + (-1)/2 = (-3)/4$

take away directed numbers

Integer Subtraction -- First Principles : Directed whole numbers subtraction is taking away an amount from another with direction information taken into account.

Examples are :
• from $received: 5$ $text(received:)5$ , taking away $received: 2$ $text(received:)2$ is equivalently, combining $received: 5$ $text(received:)5$ and $given: 2$ $text(given:)2$ ;
$5 - 2 = 5 + (- 2)$ $5-2 = 5+(-2)$
• from $received: 5$ $text(received:)5$ , taking away $given: 2$ $text(given:)2$ is equivalently, combining $received: 5$ $text(received:)5$ and $received: 2$ $text(received:)2$ ;
$5 - (- 2) = 5 + (+ 2)$ $5- (-2) = 5+(+2)$
• from $given: 5$ $text(given:)5$ , taking away $received: 2$ $text(received:)2$ is equivalently, combining $given: 5$ $text(given:)5$ and $given: 2$ $text(given:)2$ ;
$(- 5) - 2 = (- 5) + (- 2)$ $(-5)- 2 = (-5)+(-2)$
• from $given: 5$ $text(given:)5$ , taking away $given: 2$ $text(given:)2$ is equivalently, combining $given: 5$ $text(given:)5$ and $received: 2$ $text(received:)2$ ;
$(- 5) - (- 2) = (- 5) + (+ 2)$ $(-5)- (-2) = (-5)+(+2)$

take away directed fractions

Subtracting $- \frac{1}{4} - \frac{1}{2}$ $-1/4 - 1/2$ .

The given fractions are unlike fractions and so are converted to like fractions.

So $\frac{- 1}{4} - \frac{1}{2}$ $(-1)/4 - 1/2$

Subtraction is converted into addition. $= \frac{- 1}{4} + \frac{- 2}{4}$ $= (-1)/4 + (-2)/4$

$= \frac{- 3}{4}$ $= (-3)/4$

connected theory

Addition of Fractions: First Principles Addition is performed only when addends are like fractions.

Any unlike fractions are converted to like fractions to perform addition.

Fractions are directed numbers, having positive and negative values. The direction information is taken into account while performing addition.

Subtraction of Fractions : first principles Subtraction by subtrahend is addition of additive inverse of subtrahend.

We learned the addition and subtraction of fractions in first principles. In whole numbers and integers, we studied simplified procedures. Let us review those procedures and develop a simplified procedure for addition and subtraction of fractions.

In whole numbers, we had studied the following.

Addition by Place-value with regrouping -- simplified procedure : Two numbers are added as per the following procedure:

• the place-value positions are arranged units under units, $10$ $10$ s under $10$ $10$ s, etc.

• the units are added and if the result has $10$ $10$ numbers, then it is carried to the $10$ $10$ s place.

• The addition is continued to the higher place-value position. addition simplified procedure The carry over is the simplification of combining $10$ $10$ of a place value to a higher place value.

Addition of Integers Simplified Procedure : Two numbers with signs positive or negative are added as follows.

sign-property of addition

• +ve $+$ $+$ +ve is whole number addition

• +ve $+$ $+$ -ve is subtraction as given below
     absolute values of the two numbers are compared
     subtract the number of smaller absolute value from the number of larger absolute value. The difference is the absolute value of the result.
     the sign of result is the sign of the number with larger absolute value

• -ve $+$ $+$ -ve is addition of absolute values with negative sign.

The addition or subtraction of absolute values in the procedure are detailed in addition by place-value and subtraction by place-value

Integer Subtraction Simplified Procedure : Sign-Property of Integer Subtraction:

Integer subtraction is handled as integer addition with addends (a) minuend and (b) the negative of subtrahend.

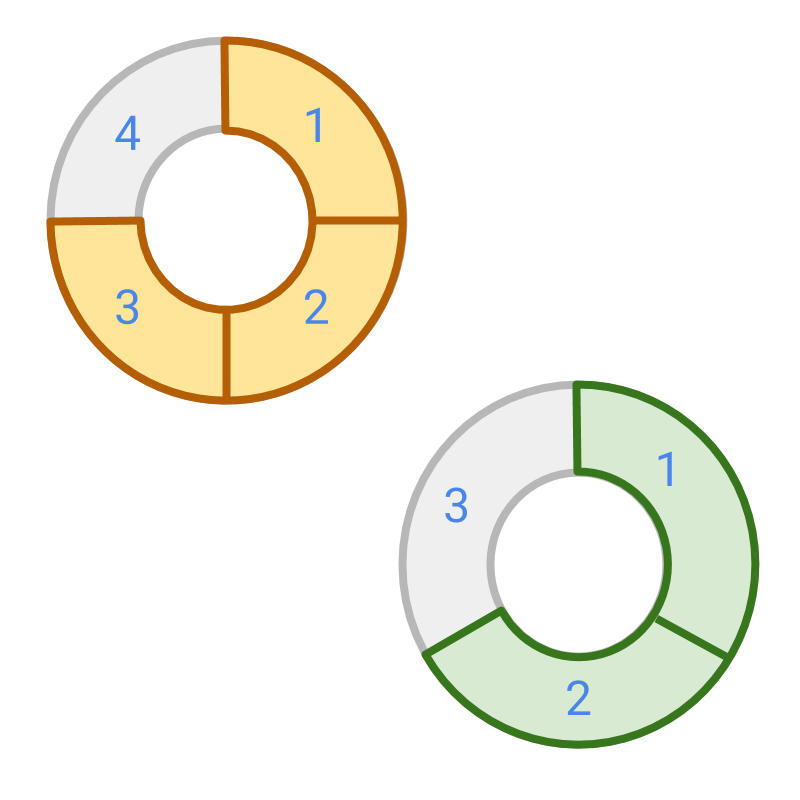
$minuend - subtrahend$ $text(minuend )-text( subtrahend )$
$= minuend as addend$ $= text( minuend as addend )$ $+ negative of subtrahend as addend$ $+ text( negative of subtrahend as addend)$

Convert Unlike to Like fractions The procedural simplification is as follows.
Two fractions $\frac{p}{q}$ $p/q$ and $\frac{l}{m}$ $l/m$ are given. Find the LCM of denominators $q$ $q$ and $m$ $m$ such that $LCM = q \times i = m \times j$ $text(LCM) = qxxi = mxxj$ . Then convert the fractions to equivalent fractions $\frac{p \times i}{q \times i}$ $(p xx i)/(q xx i)$ and $\frac{l \times j}{m \times j}$ $(l xx j)/(m xx j)$ . These are like fractions.

Addition or Subtraction of Fractions: Simplified Procedure Convert the unlike fractions to like fraction and add /subtract the numerators as integers.

Addition and subtraction of numerator uses the following from whole numbers and integers

• Sign Property of Integer addition

• Subtraction is Addition of Additive Inverse

• Whole numbers Addition by Place value

examples

Find the sum of $\frac{323}{999}$ $323/999$ and $\frac{297}{999}$ $297/999$ .
The answer is " $\frac{620}{999}$ $620/999$ ".

This problem uses the following procedures
Whole number Addition by Place Value

Find the sum of $- \frac{3}{8}$ $-3/8$ and $\frac{2}{6}$ $2/6$ .
The answer is " $- \frac{1}{24}$ $-1/24$ ".

This problem uses the following procedures
conversion into like fractions
sign property of integer addition

Find the sum of $1$ $1$ and $- \frac{1}{4}$ $-1/4$ .
The answer is " $\frac{3}{4}$ $3/4$ ". To solve this problem, the fractions are converted to like fractions and signed property of integer addition is used.

Find the difference of $- \frac{3}{8} - \frac{2}{6}$ $-3/8 - 2/6$ .
The answer is " $- \frac{17}{24}$ $-17/24$ "

This problem uses the following procedures
conversion into like fractions
conversion of subtraction into addition of negative of subtrahend
sign property of integer addition

Find the sum of $1 - \frac{- 1}{4}$ $1- (-1)/4$
The answer is " $1 \frac{1}{4}$ $1 1/4$ ".

summary

» Convert the fractions to like fractions and add numerators
→ subtraction is inverse of addition
$\frac{3}{4} + \frac{2}{3}$ $color(coral)(3/4) + color(darkgreen)(2/3)$
$= \frac{9}{12} + \frac{8}{12}$ $= color(coral)(9/12) + color(darkgreen)(8/12)$
$= \frac{17}{12}$ $= 17/12$

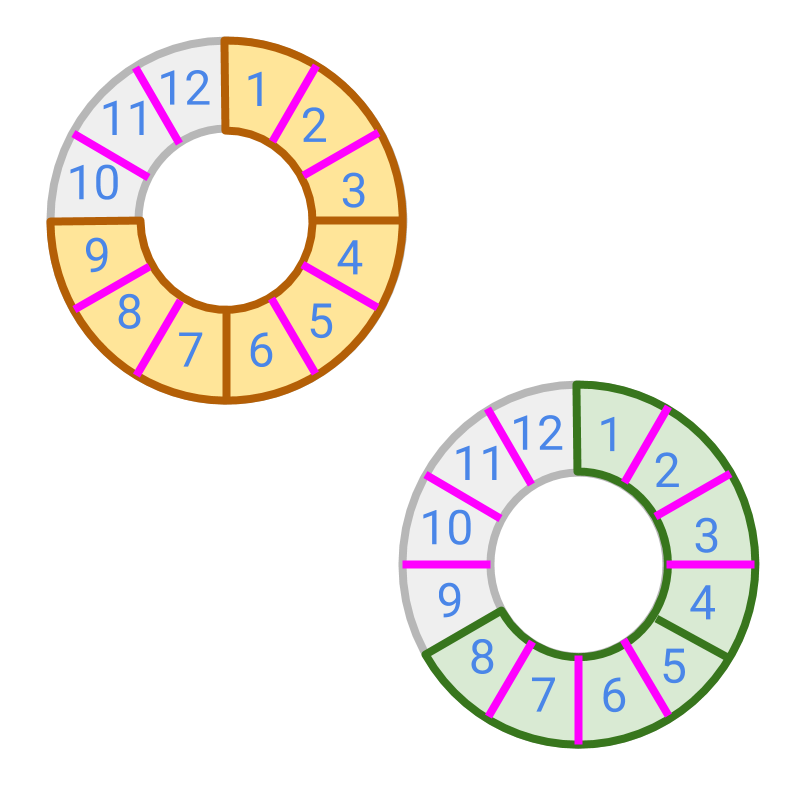
Addition or Subtraction of Fractions: Simplified Procedure Convert the unlike fractions to like fractions and add /subtract the numerators.

Addition and subtraction of numerator uses the following from whole numbers and integers

• Sign Property of Integer addition

• Subtraction is Addition of Additive Inverse

• Whole numbers Addition by Place value

Outline

The outline of material to learn "fractions" is as follows.

• click here for detailed outline of Fractions

→ Part of whole

→ Dividing a group

→ Fractions as Directed numbers

→ Like and Unlike Fractions

→ Proper and Improper Fractions

→ Equivalent & Simplest form

→ Converting unlike and like Fractions

→ Simplest form of a Fraction

→ Comparing Fractions

→ Addition & Subtraction

→ Multiplication

→ Reciprocal

→ Division

→ Numerical Expressions with Fractions

→ PEMA / BOMA