
what you'll learn...
overview
Fractions are part of whole. Division is dividing a number into equal parts.
• division in first principles -- splitting a quantity into a number of parts and measuring one part
• simplified procedure : Division as multiplication by reciprocal
just know this
Division is the inverse of multiplication. And division of fractions can be easily explained with that.
(multiply by inverse)
.
A learner may stop at this, but I would suggest to read the rest (too long, too hard) to understand how division works for fractions.
or understand this
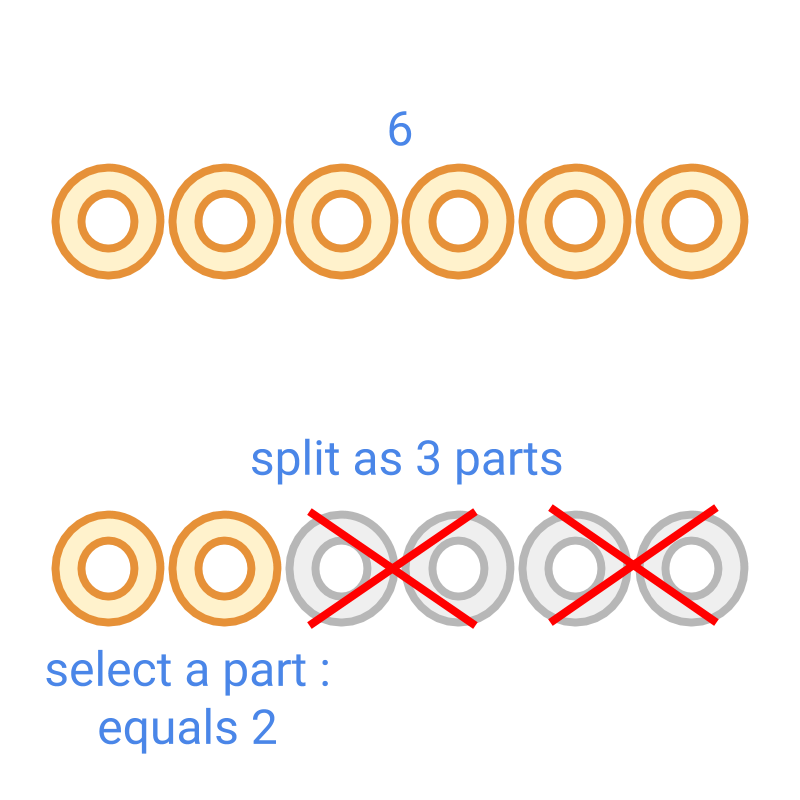
Division is illustrated in the figure.
• is the dividend
• is the divisor
• is the quotient
Dividend is split into divisor parts and one part of that is the quotient.
One way to understand the integer division:
• Dividend is considered as parts
• in that is the divisor
• In the parts one part is taken.
The key in this explanation is " dividend is considered as divisor parts and one part is taken". The same can be extended for fractions.
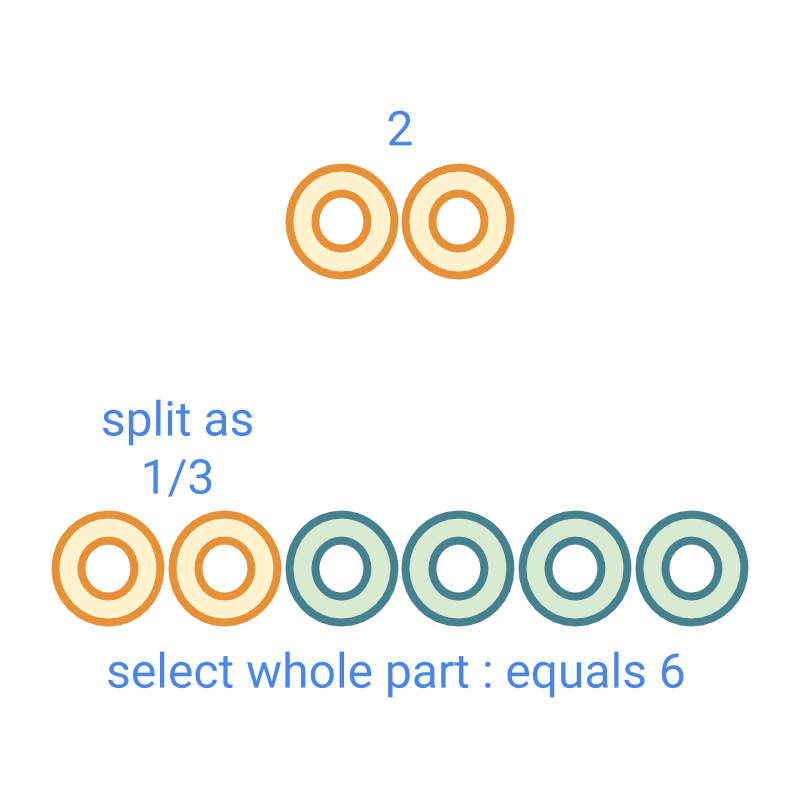
Division is illustrated in the figure.
Dividend is split as divisor parts. That is is the fraction and the full part for the fraction is found. The part is repeated to get the full part. This is shown in the figure.
In this, one part is the quotient.
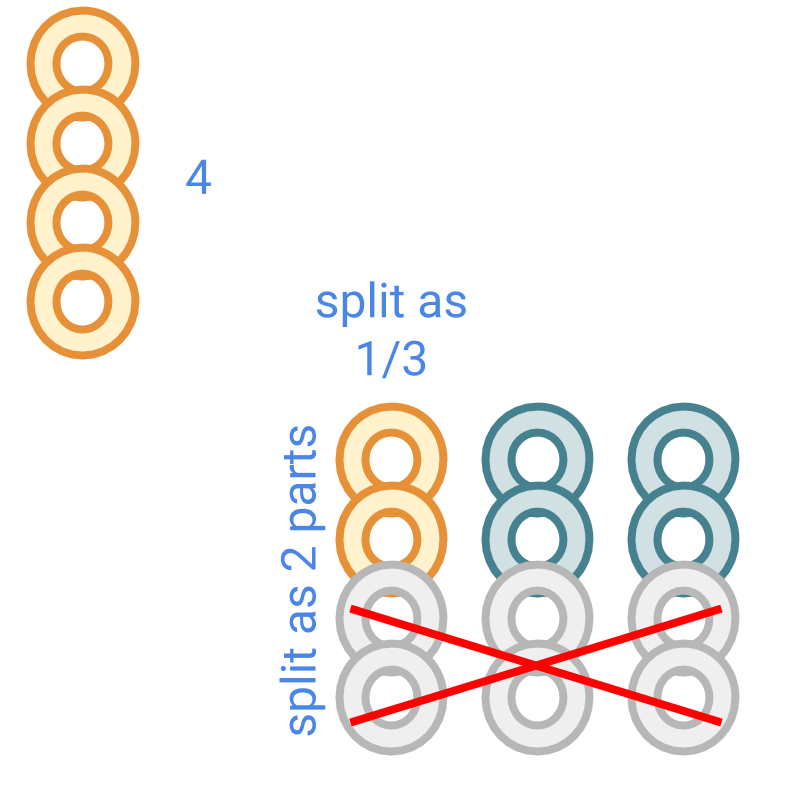
Division is illustrated in the figure.
Dividend is split as divisor parts.
In this, one part is the quotient.

Division is considered. The figure shows the dividend . The division is illustrated in the next page.
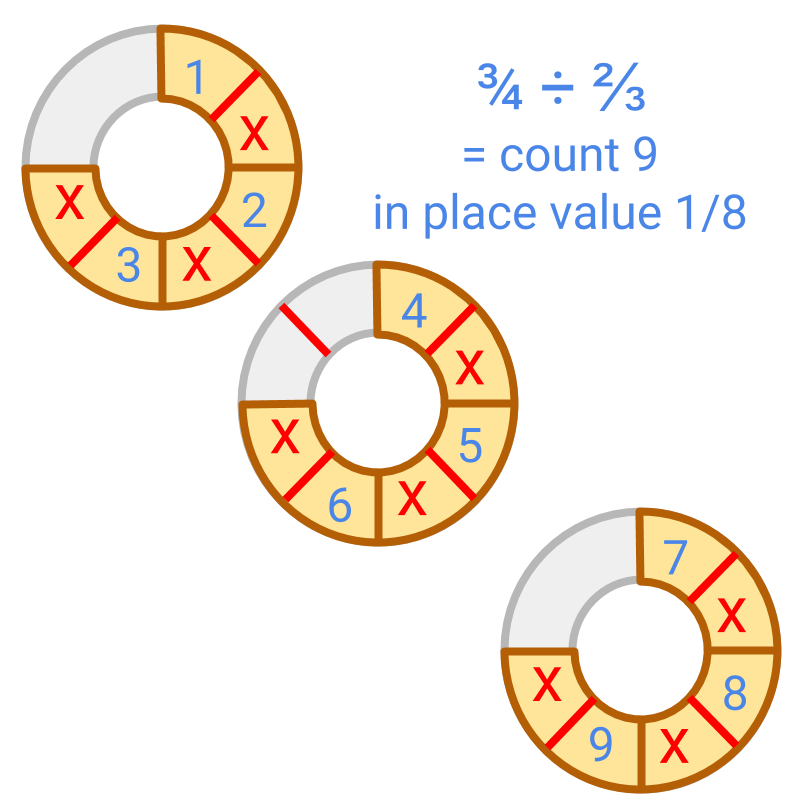
Division is illustrated in the figure.
Dividend is split as divisor parts. This is shown in the figure.
In this, the place value is and the count is 9.
The same can be simplified as follows.
yeah! enough of that
Division is inverse of multiplication.
Division of Fractions: Given two fractions and , the division is
example
Divide .
The answer is ''
summary
» =
»
 → is parts and find the group representing part
→ is parts and find the group representing part
→
»
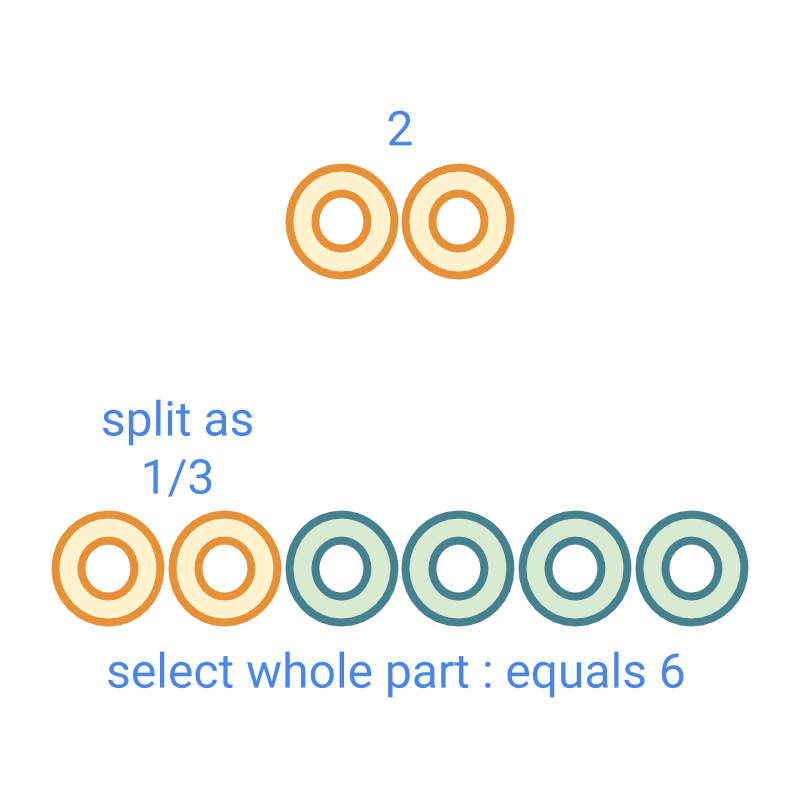 → is part and find the group representing part
→ is part and find the group representing part
→
»
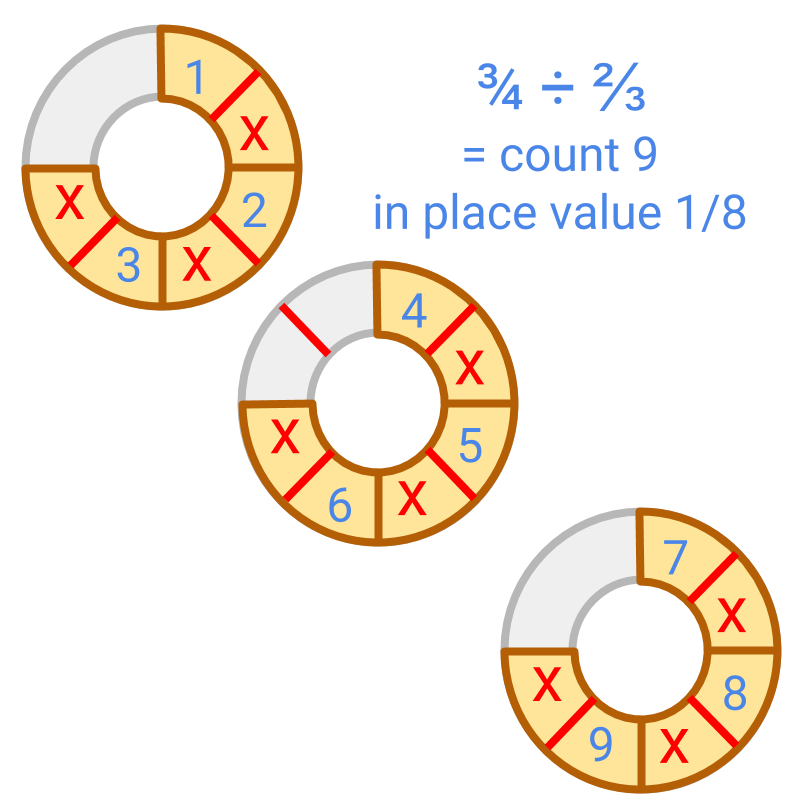 → is part and find the group representing part
→ is part and find the group representing part
→
Making sense of the first principles of division by fraction is one of the exhilarating experiences of learning.
» Procedural Simplification: Division is multiplication by inverse
→
→
→
Outline
The outline of material to learn "fractions" is as follows.
• click here for detailed outline of Fractions
→ Part of whole
→ Dividing a group
→ Fractions as Directed numbers
→ Like and Unlike Fractions
→ Proper and Improper Fractions
→ Equivalent & Simplest form
→ Converting unlike and like Fractions
→ Simplest form of a Fraction
→ Comparing Fractions
→ Addition & Subtraction
→ Multiplication
→ Reciprocal
→ Division
→ Numerical Expressions with Fractions
→ PEMA / BOMA