Fractions : Comparing Fractions

maths > fractions

Comparing Fractions

what you'll learn...

overview

In this, Comparing two fractions of different place values or denominators is explained. This covers

• comparing like fractions by the value of numerators.

• When comparing numerators, the integer comparison principles / procedures are applied.

• fractions in number line

• ascending and descending order of fractions

compare whole

Let us quickly review comparing whole numbers and set on to understand comparing fractions.

The number $7$ $7$ is "larger" than the number $3$ $3$ .

The number $4$ $4$ is "smaller" than the number $6$ $6$ .

The number $5$ $5$ is "equal" to the number $5$ $5$ .

In whole numbers, we had studied the following.

Trichotomy Property of Comparison : Two numbers can be compared to find one of them as

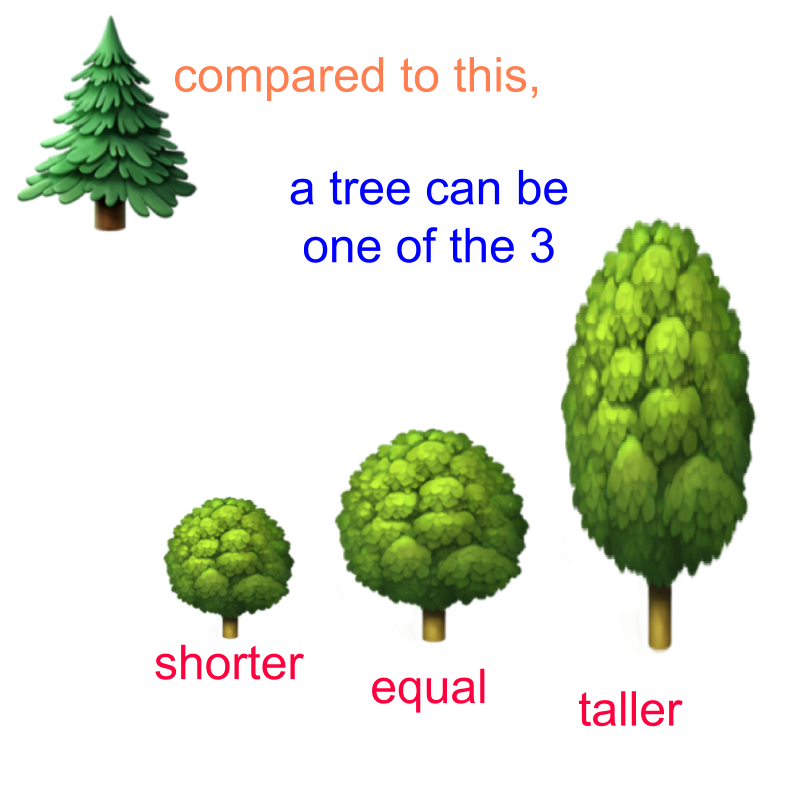
• smaller or less

• equal

• greater or larger

Comparison by First Principle: Two quantities are matched one-to-one and compared in the count or magnitude of the quantities. As a result one of them is smaller or equal to or larger to the other. 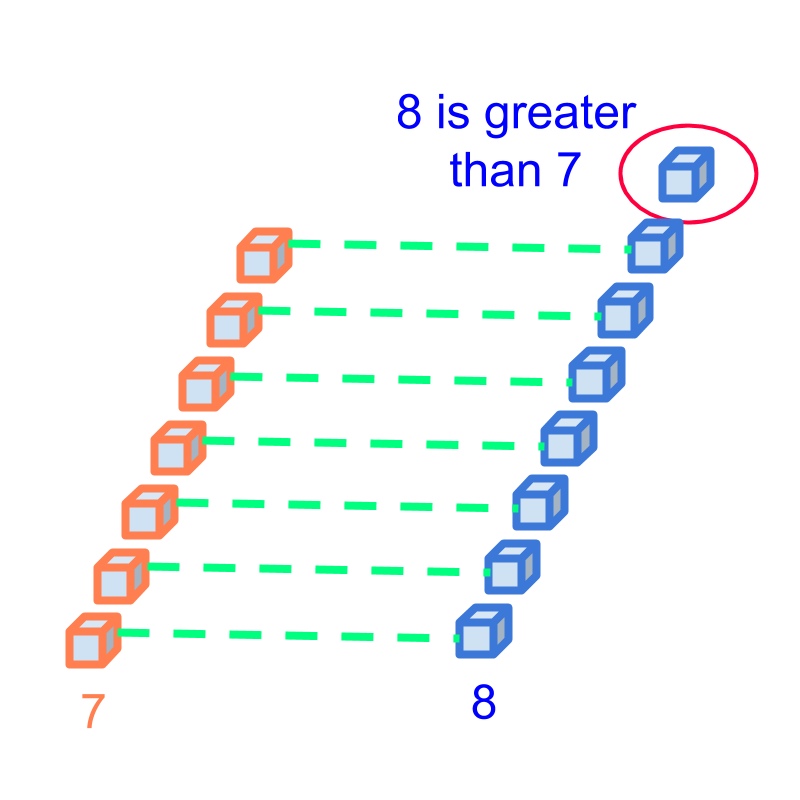whole number comparison Example: Comparing the numbers $7$ $7$ and $8$ $8$ . The quantities represented by them is compared in the figure. It is found that $7$ $7$ is smaller than $8$ $8$ .

Simplified Procedure -- Comparison by ordered-sequence: To find if one numbers is larger or smaller than another number, the numbers are compared using the order $0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, \dots$ $0,1,2,3,4,5,6,7,8,9, 10, cdots$ . comparing on number line Example: Comparing the numbers $4$ $4$ and $7$ $7$ .

$4$ $4$ is on the left-side to $7$ $7$ in the order $0, 1, 2, 3, 4, 5, 6, 7, 8, 9$ $0,1,2,3,4,5,6,7,8,9$ and so $4$ $4$ is smaller than $7$ $7$ .

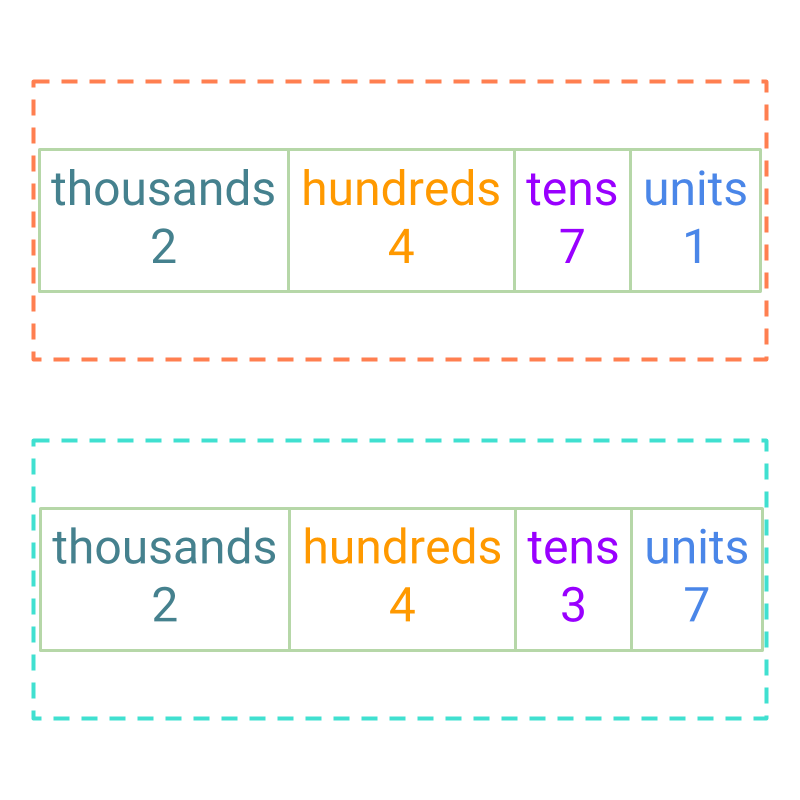
Comparison by Place-value -- Simplified Procedure to Compare Large Numbers: To find if one number is larger or smaller than another number, the digits at the highest place value are compared and if they are equal, then the digits at next lower place value are compared. comparing numbers simplified procedure

Given two whole numbers, they can be compared as

• greater or larger

• smaller or lesser

• equal.

Can such comparison be done on two fractions?

compare parts

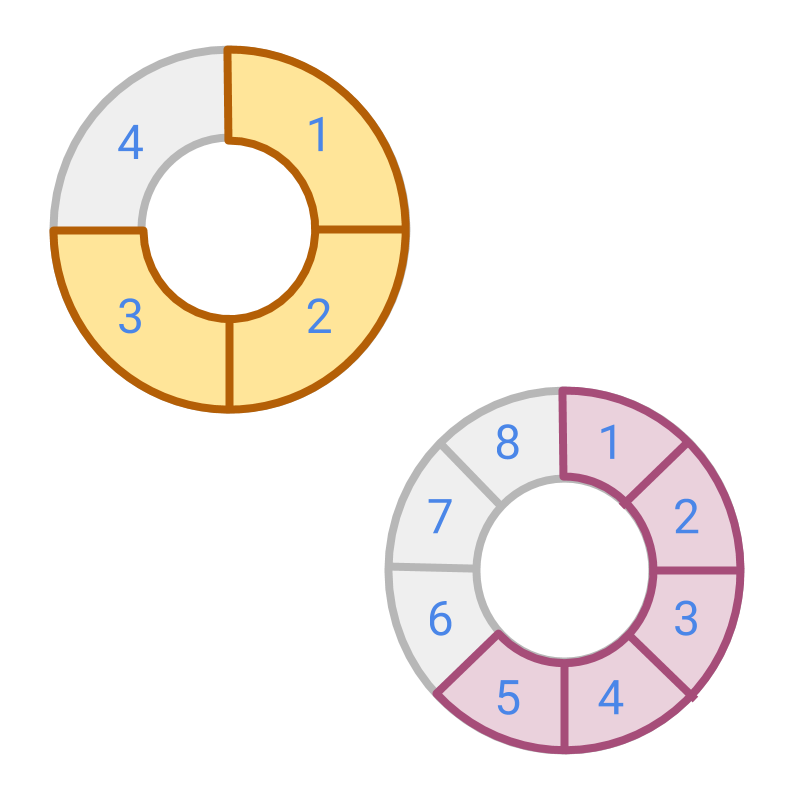
Given two fractions $\frac{1}{8}$ $1/8$ and $\frac{1}{12}$ $1/12$ . The figure shows the fractions. $\frac{1}{8}$ $1/8$ is shown in brown, and $\frac{1}{12}$ $1/12$ is shown in purple color.

Comparing the quantities represented by the fractions, it is concluded that $\frac{1}{8}$ $1/8$ is larger than $\frac{1}{12}$ $1/12$ .

Given two fractions $\frac{3}{4}$ $3/4$ and $\frac{5}{8}$ $5/8$ . A picture to show the quantities is not given. Can these be compared?

Given two fractions $\frac{3}{4}$ $3/4$ and $\frac{5}{8}$ $5/8$ .

The figure shows the fractions. $\frac{3}{4}$ $3/4$ is shown in brown, and $\frac{5}{8}$ $5/8$ is shown in purple color.

With the figure, it is easy to find that one fraction is larger than another.
To compare these fractions, convert the fractions to like fractions having same place value

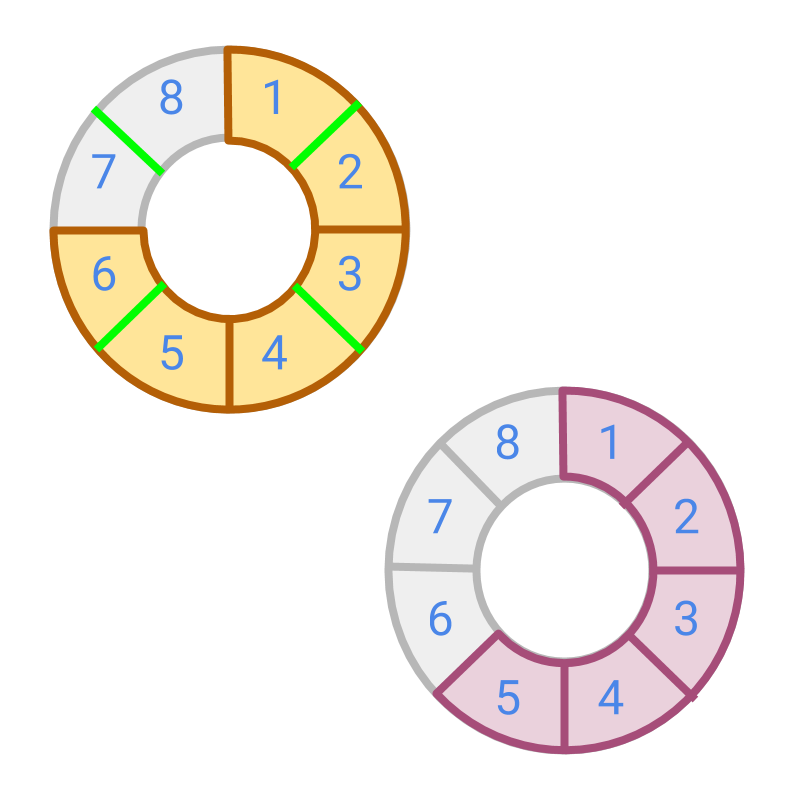
Given two fractions $\frac{3}{4}$ $3/4$ and $\frac{5}{8}$ $5/8$ . The fraction $\frac{3}{4}$ $3/4$ is converted to $\frac{6}{8}$ $6/8$ to make them like fractions.

Both $\frac{6}{8}$ $6/8$ and $\frac{5}{8}$ $5/8$ have the same place value $\frac{1}{8}$ $1/8$ (ie: same denominator $8$ $8$ ).

In this form, the numerators can be compared and $\frac{6}{8}$ $6/8$ is larger, which means its equivalent fraction $\frac{3}{4}$ $3/4$ is larger than $\frac{5}{8}$ $5/8$ .

Two fractions can be compared by numerators after converting them into like fractions.

In whole numbers, $2$ $2$ tens and $8$ $8$ units are compared by converting $2$ $2$ tens into $20$ $20$ units. $20$ $20$ units is larger than $8$ $8$ units.

In fractions, the denominators represent the place values, and numbers of same place value can be compared. Numerators of like fractions are compared as whole numbers, and unlike fractions are converted to like fractions before the comparison.

Comparing fractions: First principles The numerators of two like fractions can be compared as whole numbers.

Unlike fractions are first converted into like fractions to compare them.

example

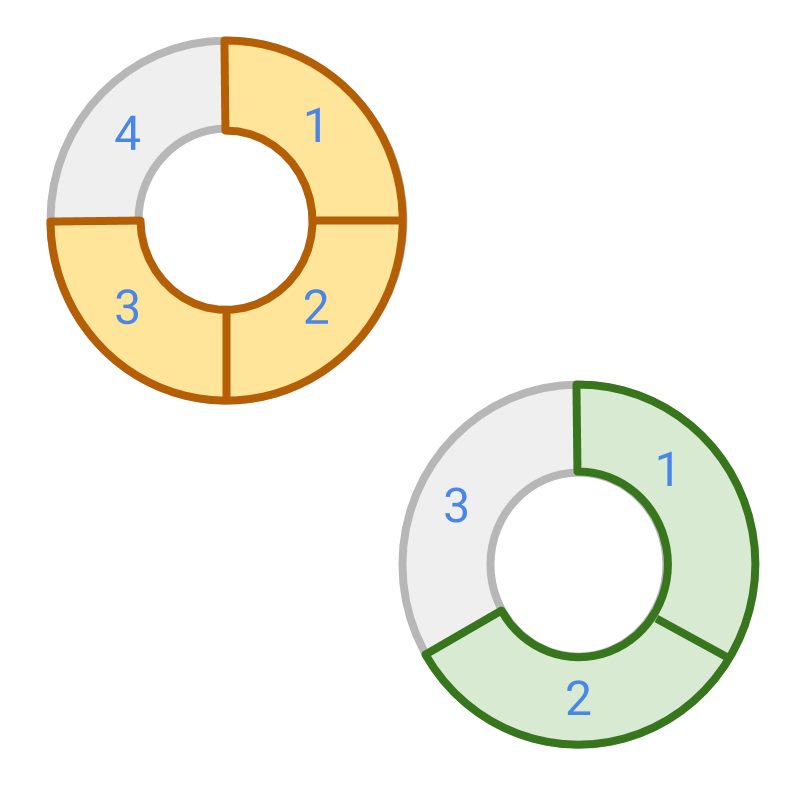
Given $\frac{3}{4}$ $3/4$ and $\frac{2}{3}$ $2/3$ , Which fraction is smaller?
The answer is ' $\frac{2}{3}$ $2/3$ '. First, convert them to like fractions

$LCM (4, 3) = 12$ $text(LCM)(4,3) = 12$

$\frac{3}{4} = \frac{9}{12}$ $3/4 = 9/12$

$\frac{2}{3} = \frac{8}{12}$ $2/3 = 8/12$

Comparing the numerators $9$ $9$ and $8$ $8$ , it is concluded that $\frac{2}{3}$ $2/3$ is smaller.

compare directed numbers

So far only positive fractions were considered for comparison. Fractions are directed numbers too. Fractions can be either positive or negative. Let us see how to compare such fractions.

Comparison of Integers -- First Principles: : Comparison is in terms of the amount received (or the aligned direction).

Amount given is smaller than amount received, as comparison is by amount received.

Larger amount given is smaller than smaller amount given, as comparison is by the amount received.

Comparison of Integers -- Simplified Procedure:

sign-property of comparison
• +ve and +ve are compared as whole numbers.
• When comparing +ve and -ve, the +ve value is larger irrespective of the absolute values of the numbers.
• When comparing -ve and -ve, the number with smaller absolute value is larger than the other.

The absolute values are compared as the simplified procedure detailed in whole numbers comparison by place-value.

$\frac{3}{4}$ $3/4$ and $- \frac{6}{7}$ $-6/7$ are compared. The numbers are, $received: \frac{3}{4}$ $text(received:)3/4$ and $given: \frac{6}{7}$ $text(given:)6/7$ in directed fractions form. Received, is greater than, given.

Negative fractions are smaller than positive fractions.

Comparing $- 3$ $-3$ or $- 6$ $-6$ . The comparison is in terms of received. When comparing in terms of amount received, $given: 3$ $text(given:)3$ is larger than $given: 6$ $text(given:)6$ .

The same is applicable for fractions. Negative fraction with larger absolute value is smaller than negative fraction with smaller absolute value.

Comparison of Negative and Positive fractions: : Comparison is in terms of the amount received.

Amount given is smaller than amount received, as comparison is by amount received.

Larger amount given is smaller than smaller amount given, as comparison is by the amount received.

Simplified Procedure:

sign-property of comparison
• +ve and +ve are compared as larger absolute value is larger fraction in value.
• When comparing +ve and -ve, the +ve value is larger irrespective of the absolute values of the numbers.
• When comparing -ve and -ve, the number with smaller absolute value is larger than the other.

examples

Which of the following is smaller than the other? $\frac{1}{2}$ $1/2$ or $- \frac{2}{3}$ $-2/3$
The answer is " $- \frac{2}{3}$ $-2/3$ ." As per sign property of comparison, the negative number is smaller than the positive number.

Which of the following is smaller than the other? $- \frac{1}{2}$ $-1/2$ or $- \frac{3}{4}$ $-3/4$
The answer is " $- \frac{3}{4}$ $-3/4$ "

Both the numbers are negative. So, the larger amount in negative is smaller in values. Comparing the numbers without the sign and converting them to like fractions, $\frac{3}{4}$ $3/4$ is larger in value and so $- \frac{3}{4}$ $-3/4$ is smaller than $- \frac{1}{2}$ $-1/2$ .

Which of the following is larger than the other? $- \frac{3}{4}$ $-3/4$ or $- \frac{3}{4}$ $-3/4$
The answer is "the numbers are equal"

Which of the following is larger than the other? $\frac{3}{4}$ $3/4$ or $- \frac{3}{4}$ $-3/4$
The answer is " $\frac{3}{4}$ $3/4$ ". As per sign property of comparison, the positive number is larger than the negative number.

order in parts

In whole numbers, we learned that the ordinal-property of the numbers is defined by `0<1<2<3
In integers, we learned that the ordinal-property of the numbers is extended to $\dots < - 3 < - 2 < - 1 < 0$ $cdots <-3<-2<-1<0$ $< 1 < 2 < 3 < \dots$ $<1<2<3< cdots$ .

Let us see how the ordinal property is extended to fractions.

To understand the ordinal property of fractions, let us first consider fractions of same denominator. The ordinal property is readily extended to

$\dots < \frac{- 3}{5} < \frac{- 2}{5} < \frac{- 1}{5} < 0$ $cdots <(-3)/5<(-2)/5<(-1)/5<0$ $< \frac{1}{5} < \frac{2}{5} < \frac{3}{5} < \dots$ $<1/5<2/5<3/5< cdots$

$numberline of fractions$

The ordinal property is best captured by the number-line.

• Number-line of whole numbers starts from $0$ $0$ and extends in one direction. It consists of points at positions $0, 1, 2, \dots$ $0,1,2, cdots$ .

• Number-line of integers extends in both the directions. It consists of points at positions $\dots, - 2, - 1, 0, 1, 2, \dots$ $cdots, -2,-1,0,1,2, cdots$

• Fractions are placed between the integers values. Number-line of fractions extends in both the directions.

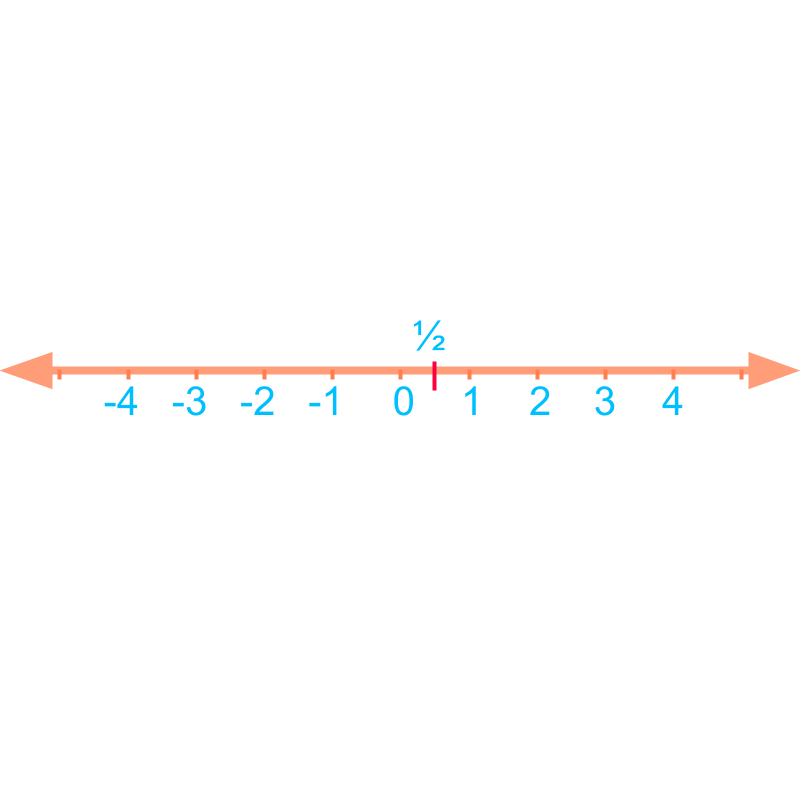
$numberline of fractions$

Consider the number line of fractions. $\frac{1}{2}$ $1/2$ is placed between points $0$ $0$ and $1$ $1$ .

The line-segment between $0$ $0$ and $1$ $1$ is split into $2$ $2$ equal pieces. $\frac{1}{2}$ $1/2$ is at the position of $1$ $1$ piece as shown in the figure.

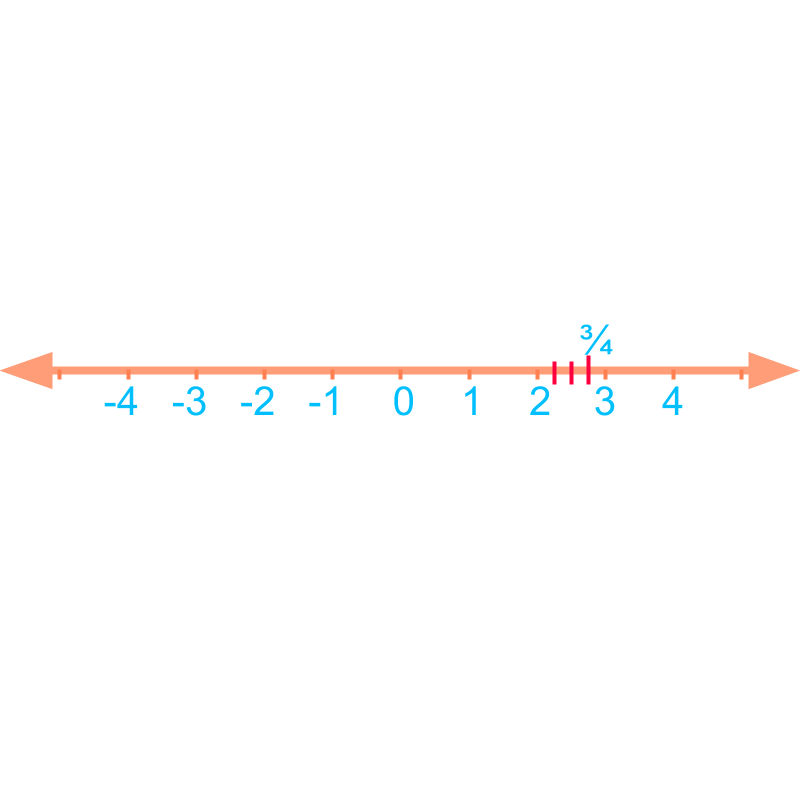
$numberline of fractions$

The fraction $2 \frac{3}{4}$ $2 3/4$ , is placed between points $2$ $2$ and $3$ $3$ at third position of $4$ $4$ pieces. The line-segment between $2$ $2$ and $3$ $3$ is split into $4$ $4$ equal pieces. $2 \frac{3}{4}$ $2 3/4$ is at the position of third piece as shown in the figure.

largest and smallest

Given several fractions, to compare as largest or smallest, the fractions are converted to like fractions.

The ascending order was introduced in whole numbers. Given numbers are arranged from smallest to largest.

The descending order was introduced in whole numbers. Given numbers are arranged from largest to smallest.

Two or more fractions can be arranged in ascending order or descending order, after converting them to like fractions. The like fractions can be ordered based on the value of the numerators.

Two or more fractions can be compared to arrange them in
• ascending order : from the smallest to the largest
• descending order : from the largest to the smallest

examples

Arrange the numbers in ascending order $- \frac{23}{4}$ $-23/4$ , $\frac{7}{3}$ $7/3$ , $\frac{42}{3}$ $42/3$ .
The answer is " $- \frac{23}{4}$ $-23/4$ , $\frac{7}{3}$ $7/3$ , $\frac{42}{3}$ $42/3$ "

Arrange the numbers in descending order $\frac{8}{5}$ $8/5$ , $\frac{9}{10}$ $9/10$ , $- \frac{9}{2}$ $-9/2$ .
The answer is " $\frac{8}{5}$ $8/5$ , $\frac{9}{10}$ $9/10$ , $- \frac{9}{2}$ $-9/2$ "

Arrange the numbers in descending order $\frac{2}{27}$ $2/27$ , $\frac{2}{9}$ $2/9$ , $\frac{2}{36}$ $2/36$ .
The answer is " $\frac{2}{9}$ $2/9$ , $\frac{2}{27}$ $2/27$ , $\frac{2}{36}$ $2/36$ "

summary

» convert the fractions to like fractions and compare the numerators.
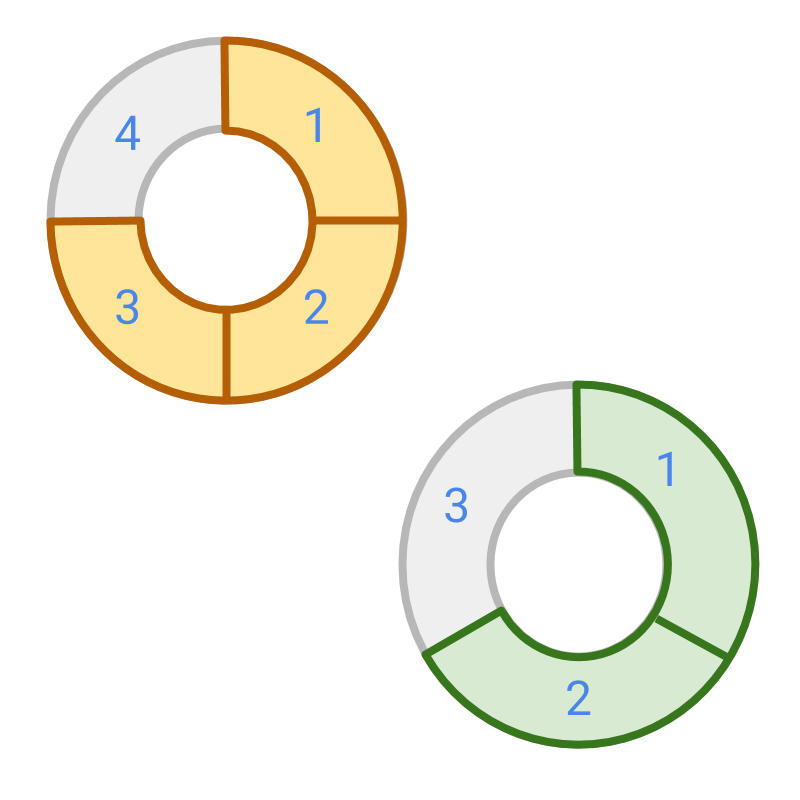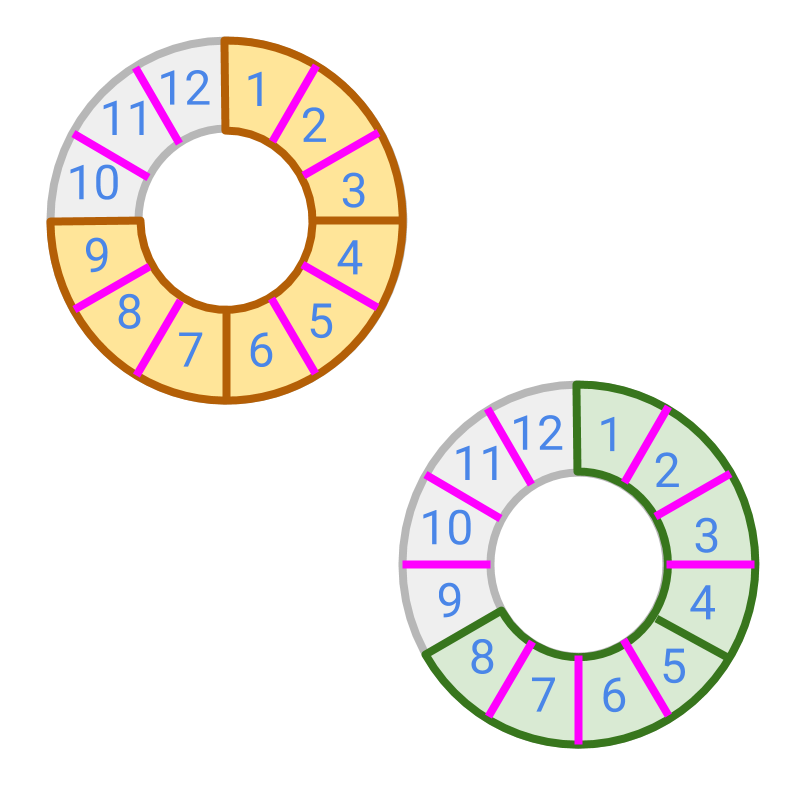   → $\frac{3}{4} ? \frac{2}{3}$ $color(coral)(3/4) ? color(darkgreen)(2/3)$
   → $\frac{3}{4} = \frac{9}{12}$ $color(coral)(3/4 = 9/12)$ and $\frac{2}{3} = \frac{8}{12}$ $color(darkgreen)(2/3 = 8/12)$
   → $9 > 8$ $color(coral)(9) > color(darkgreen)(8)$ $\Rightarrow$ $rArr$ $\frac{9}{12} > \frac{8}{12}$ $color(coral)(9/12) > color(darkgreen)(8/12)$
   → $\frac{3}{4} > \frac{2}{3}$ $color(coral)(3/4) > color(darkgreen)(2/3)$

In comparing numerators as integers, the following principles / procedures of integer comparion is used.
• Comparison by First Principle
• Simplified Procedure -- Comparison by ordered-sequence
• Comparison by Place-value
• sign-property of comparison

Outline

The outline of material to learn "fractions" is as follows.

• click here for detailed outline of Fractions

→ Part of whole

→ Dividing a group

→ Fractions as Directed numbers

→ Like and Unlike Fractions

→ Proper and Improper Fractions

→ Equivalent & Simplest form

→ Converting unlike and like Fractions

→ Simplest form of a Fraction

→ Comparing Fractions

→ Addition & Subtraction

→ Multiplication

→ Reciprocal

→ Division

→ Numerical Expressions with Fractions

→ PEMA / BOMA