Fractions : Converting UnLike fractions

maths > fractions

Converting UnLike fractions

what you'll learn...

overview

In this, converting unlike fractions to like fractions is explained.

• To convert unlike fractions to like fractions, convert them to equivalent fractions having same denominator or place-value.

unlike to like

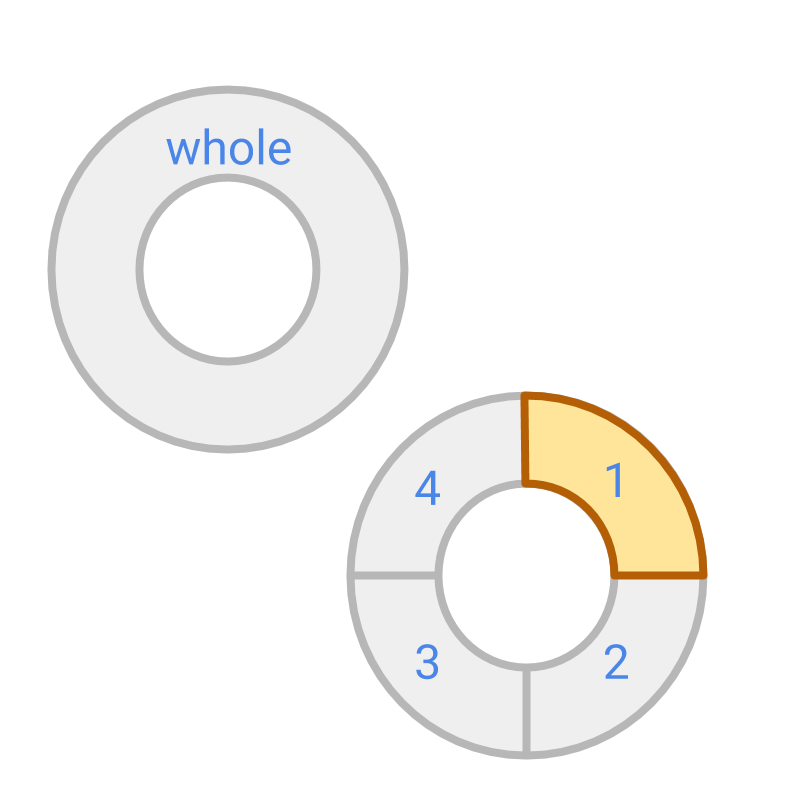
$ring fraction 1/4$

The figure shows a whole and a fraction. The fraction represented by the colored part is $\frac{1}{4}$ $1/4$

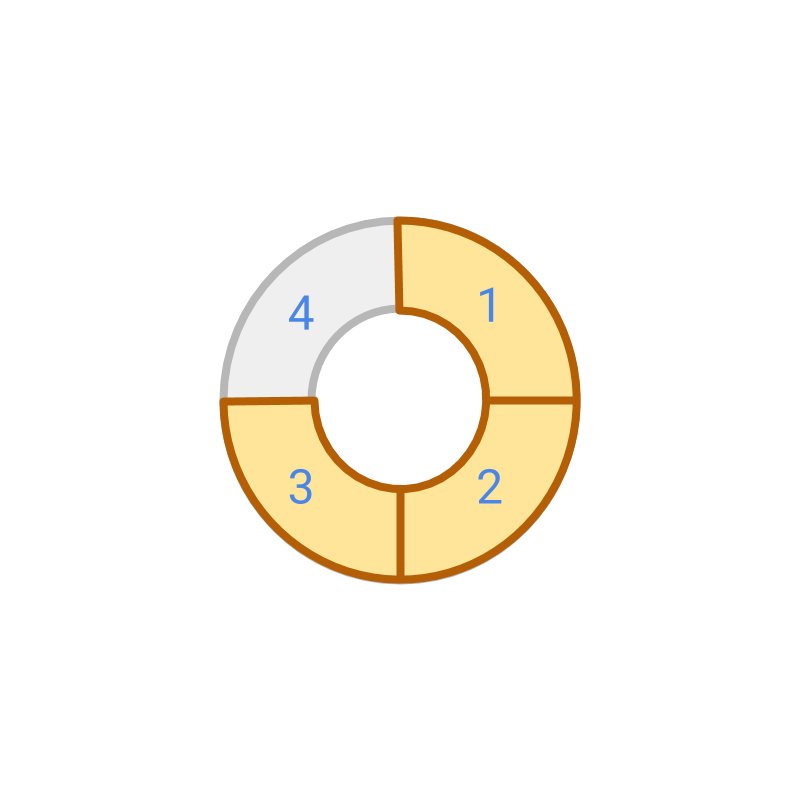
$ring fraction 3/4$

The fraction represented by the colored part is $\frac{3}{4}$ $3/4$

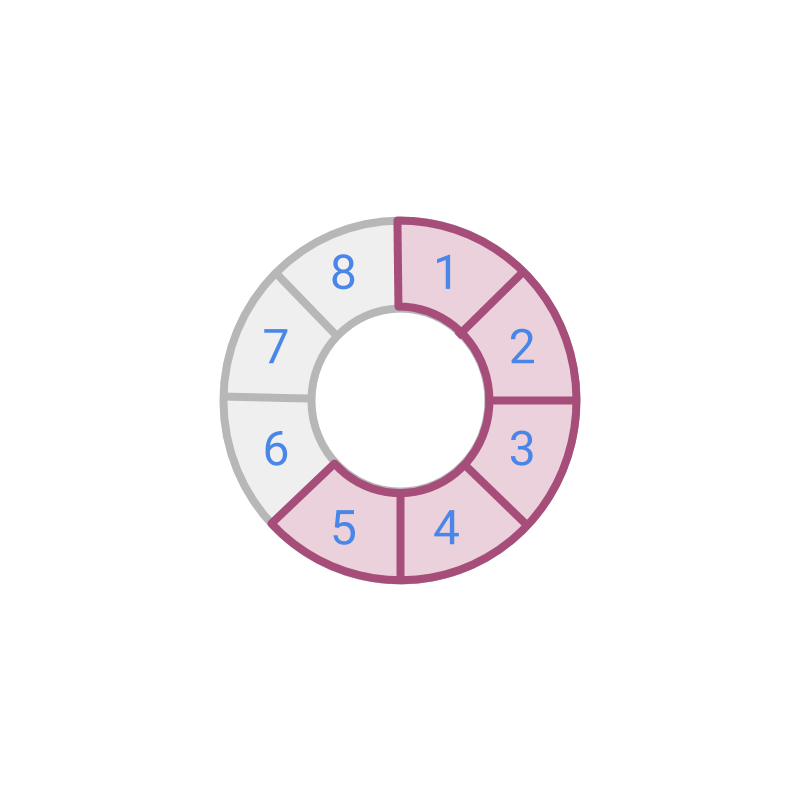
$ring fraction 5/8$

The fraction represented by the colored part is $\frac{5}{8}$ $5/8$ .

$ring fractions different place values$

The figure shows two fractions $\frac{3}{4}$ $3/4$ and $\frac{5}{8}$ $5/8$ .

These are unlike Fractions. The denominators are $4$ $4$ and $8$ $8$ , so the place values are different.

If the parts of the first fraction is cut into two pieces. The place value of one fraction can be modified to match the other fraction. The two fractions are converted into like fractions.

$converting unlike fraction to like fractions$

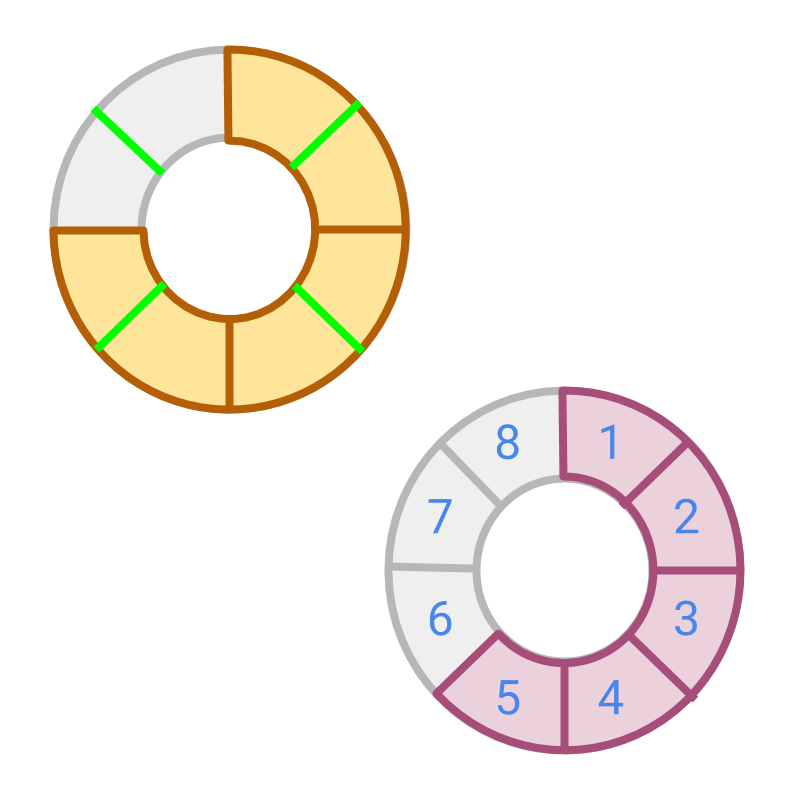
The figure shows two fractions $\frac{3}{4}$ $3/4$ and $\frac{5}{8}$ $5/8$ . If the fraction having place value $\frac{1}{4}$ $1/4$ is modified to have place value $\frac{1}{8}$ $1/8$ , then these fractions will be like fractions. The conversion is shown in the figure.

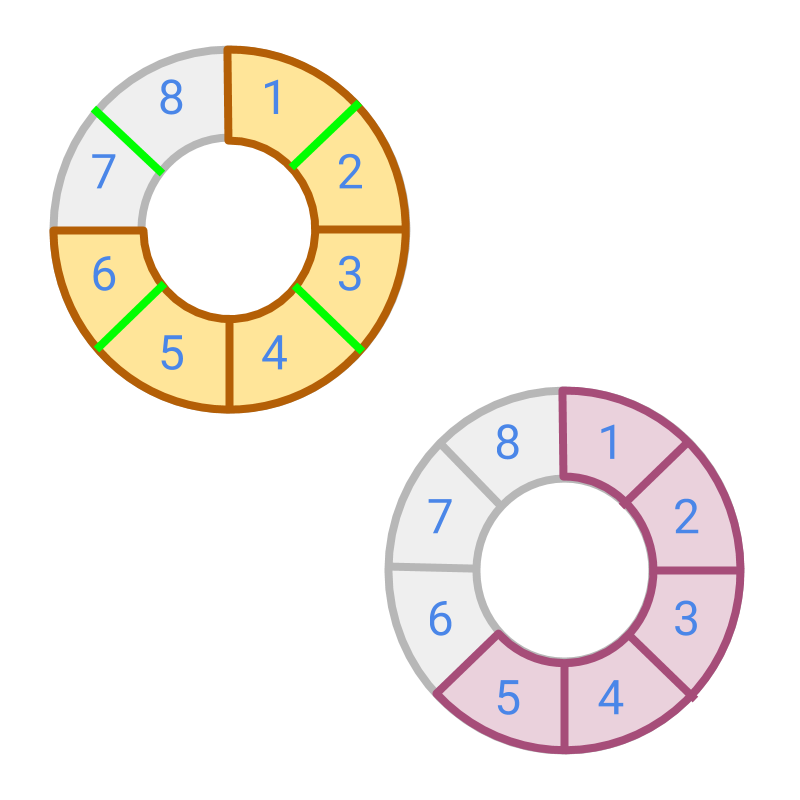
$converting unlike fraction to like fractions$

After converting the fraction to have same place value, the number represented by fraction is found. The figure shows the two fractions. The converted fractions are $\frac{6}{8}$ $6/8$ and $\frac{5}{8}$ $5/8$ . These are like fractions.

a lot unlike

$ring fraction 2/3$

Representation of fraction $\frac{2}{3}$ $2/3$ is shown in the figure.

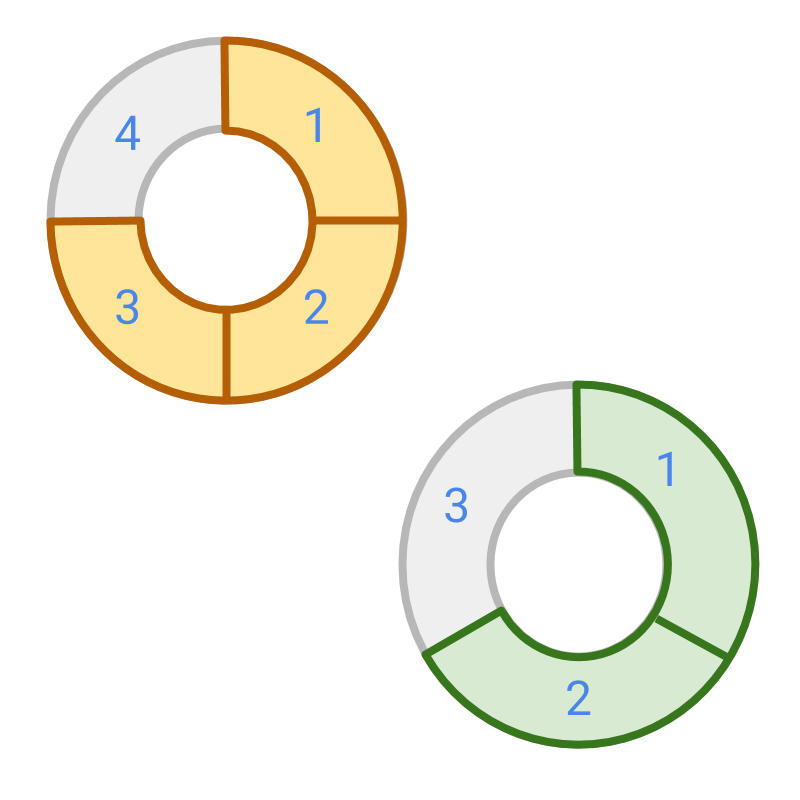
$ring fractions different place values$

The figure shows two fractions $\frac{3}{4}$ $3/4$ and $\frac{2}{3}$ $2/3$ . The objective is to convert them to like fractions.

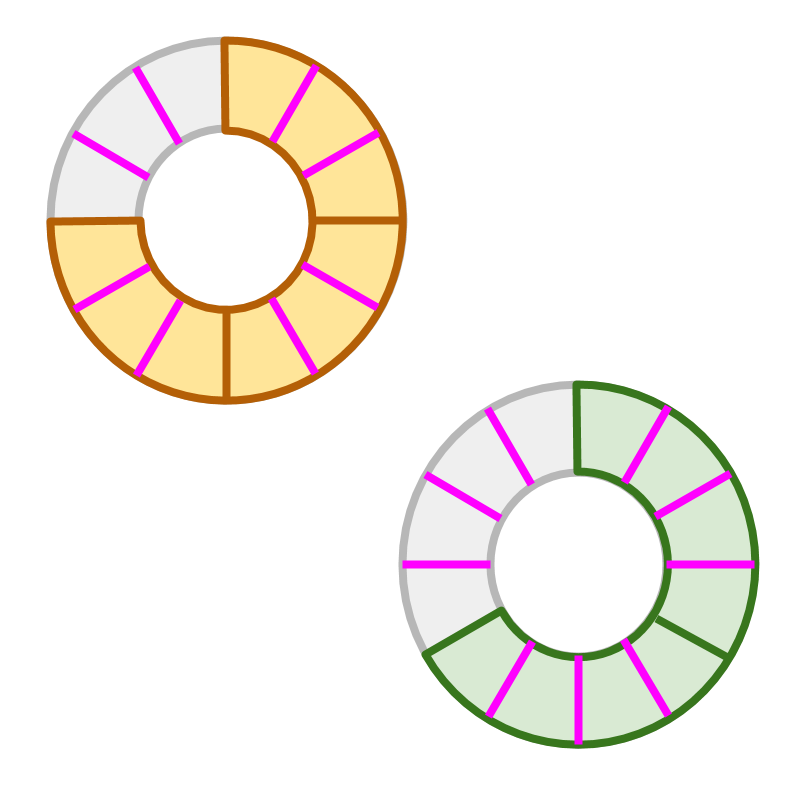
$converting unlike fraction to like fractions$

The denominators are $4$ $4$ and $3$ $3$ . To make them like fractions, the place value is chosen to be the common multiple of the denominators. The conversion is shown in the figure.

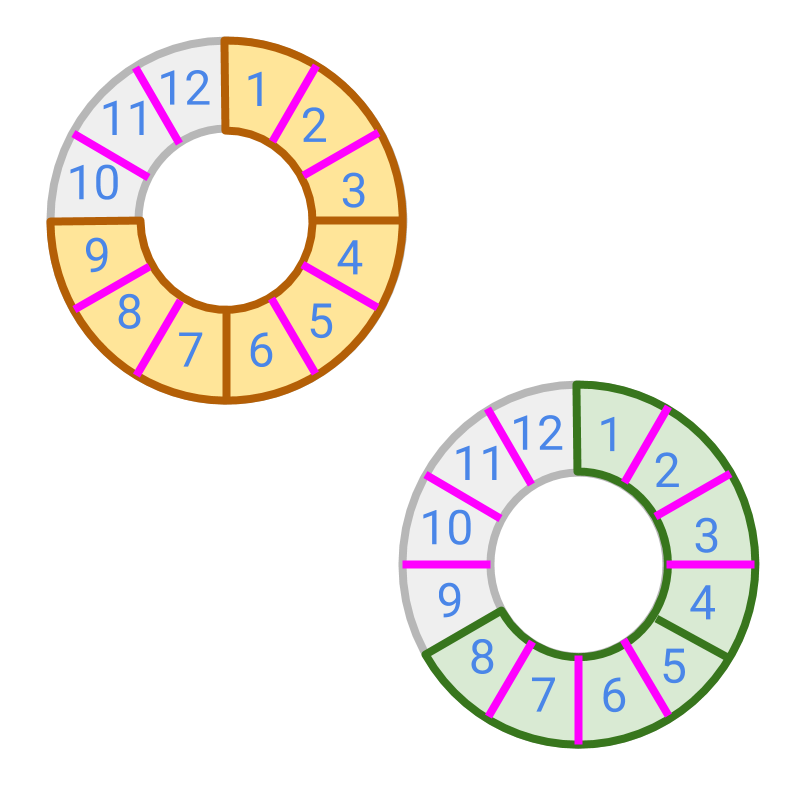
$converting unlike fraction to like fractions$

After converting the fraction to have the same place value, the number represented by fraction is found.

The figure shows the two fractions. The converted fractions are $\frac{9}{12}$ $9/12$ and $\frac{8}{12}$ $8/12$ . These are like fractions.

This process involves finding equivalent fractions of the given fractions. The place value or the denominator is chosen to be equal.

$\frac{3}{4} = \frac{3 \times 3}{4 \times 3} = \frac{9}{12}$ $3/4 = (3xx3)/(4xx3) = 9/12$

$\frac{2}{3} = \frac{2 \times 4}{3 \times 4} = \frac{8}{12}$ $2/3 = (2xx4)/(3xx4) = 8/12$

An example of conversion of unlike fractions to like fraction is shown in the figure.

To convert the fractions to the same place value,
• the fractions are to be converted to equivalent fractions.
• the "least common multiple" of denominators is found and
• the denominators of the given fractions are converted to the multiple
• when modifying denominators, numerators are modified accordingly.

To convert unlike fractions to like fractions, convert them to equivalent fractions having same denominator or place-value.

Convert Unlike to Like fractions The procedural simplification is as follows.
Two fractions $\frac{p}{q}$ $p/q$ and $\frac{l}{m}$ $l/m$ are given. Find the LCM of denominators $q$ $q$ and $m$ $m$ such that $LCM = q \times i = m \times j$ $text(LCM) = qxxi = mxxj$ . Then convert the fractions to equivalent fractions $\frac{p \times i}{q \times i}$ $(p xx i)/(q xx i)$ and $\frac{l \times j}{m \times j}$ $(l xx j)/(m xx j)$ . These are like fractions.

summary

» Convert to equivalent fractions with LCM of denominators as the denominator
→ eg: $\frac{3}{4}$ $3/4$ and $\frac{2}{3}$ $2/3$
→ eg: $\frac{9}{12}$ $9/12$ and $\frac{8}{12}$ $8/12$

Outline

The outline of material to learn "fractions" is as follows.

• click here for detailed outline of Fractions

→ Part of whole

→ Dividing a group

→ Fractions as Directed numbers

→ Like and Unlike Fractions

→ Proper and Improper Fractions

→ Equivalent & Simplest form

→ Converting unlike and like Fractions

→ Simplest form of a Fraction

→ Comparing Fractions

→ Addition & Subtraction

→ Multiplication

→ Reciprocal

→ Division

→ Numerical Expressions with Fractions

→ PEMA / BOMA