Fractions : Multiplication of fractions

maths > fractions

Multiplication of fractions

what you'll learn...

overview

In this page, multiplcation of fractions is explained.

• multiplication in first principles -- repeatedly combining a quantity and measuring the combined and

• simplified procedure : Multiplying numerators and denominators

repeated times

Multiplication of integers or whole numbers: $4 \times 3 = 12$ $4 xx 3 = 12$

• $4$ $4$ is the multiplicand

• $3$ $3$ is the multiplier

• $12$ $12$ is the product

Multiplication is repeating the multiplicand the multiplier times -- to get the product.
$4$ $4$ repeated $3$ $3$ times =
$4 + 4 + 4 = 12$ $4+4+4 = 12$

Multiplication by a fraction : Consider $1 \times \frac{1}{4}$ $1 xx 1/4$
Multiplicand $1$ $1$ is multiplied by a multiplier $\frac{1}{4}$ $1/4$ .

The multiplication $1 \times \frac{1}{4}$ $1 xx 1/4$ is illustrated.

The multiplicand is divided into $4$ $4$ parts (which is the place value of the multiplier) and product is calculated by selecting $1$ $1$ part (which is the numerator of the multiplier). The product is $\frac{1}{4}$ $1/4$ .

Multiplication by a fraction : Consider $2 \times \frac{1}{4}$ $2 xx 1/4$
Multiplicand $2$ $2$ is multiplied by a multiplier $\frac{1}{4}$ $1/4$ .
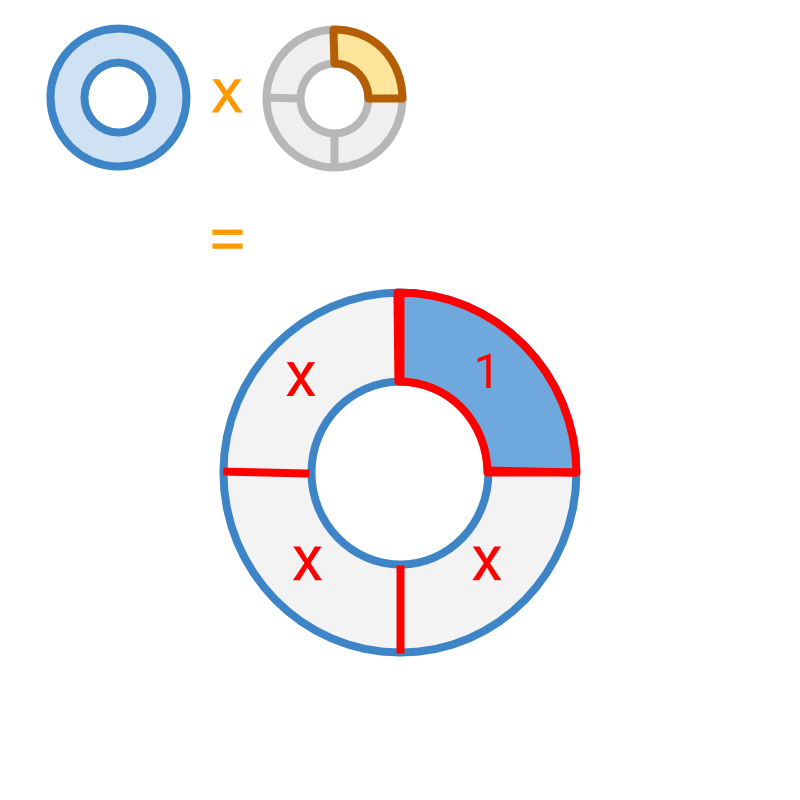
The multiplication process is illustrated in the next page.

The multiplication $2 \times \frac{1}{4}$ $2 xx 1/4$ is illustrated.

The multiplicand is divided into $4$ $4$ parts (which is the place value of the multiplier) and product is calculated by selecting $1$ $1$ part from each (which is the numerator of the multiplier).

The value of one piece with respect to a whole is $\frac{1}{4}$ $1/4$ and $2$ $2$ pieces are taken. That is, $2 pieces of \frac{1}{4} = \frac{2}{4}$ $2 text( pieces of ) 1/4 = 2/4$ .

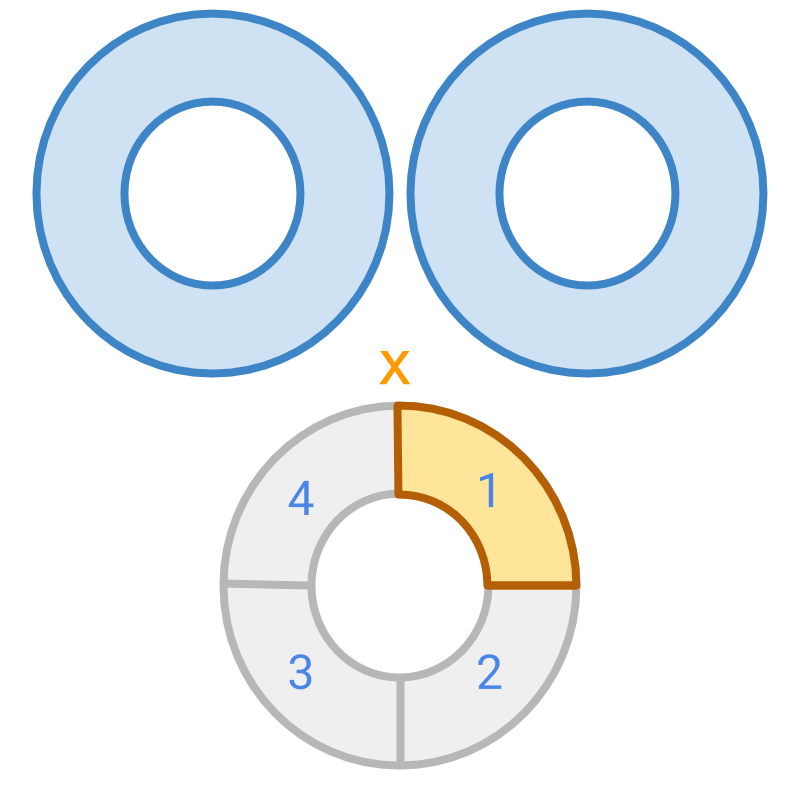
Multiplication by a fraction : Consider $1 \times \frac{3}{4}$ $1 xx 3/4$
Multiplicand $1$ $1$ is multiplied by a multiplier $\frac{3}{4}$ $3/4$ .
The multiplication process is illustrated in the next page.

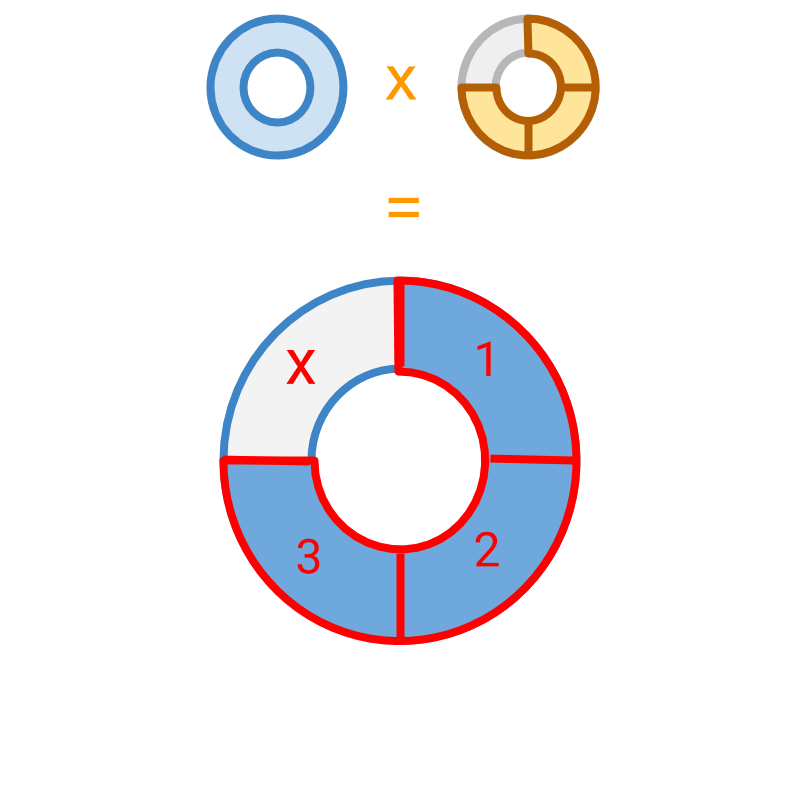
The multiplication $1 \times \frac{3}{4}$ $1 xx 3/4$ is illustrated.

The multiplicand is divided into $4$ $4$ parts (which is the place value of the multiplier) and product is found by selecting $3$ $3$ parts (which is the numerator of the multiplier).

The product is $3$ $3$ pieces in the place value $\frac{1}{4}$ $1/4$ which is $\frac{3}{4}$ $3/4$ .

fraction by fraction

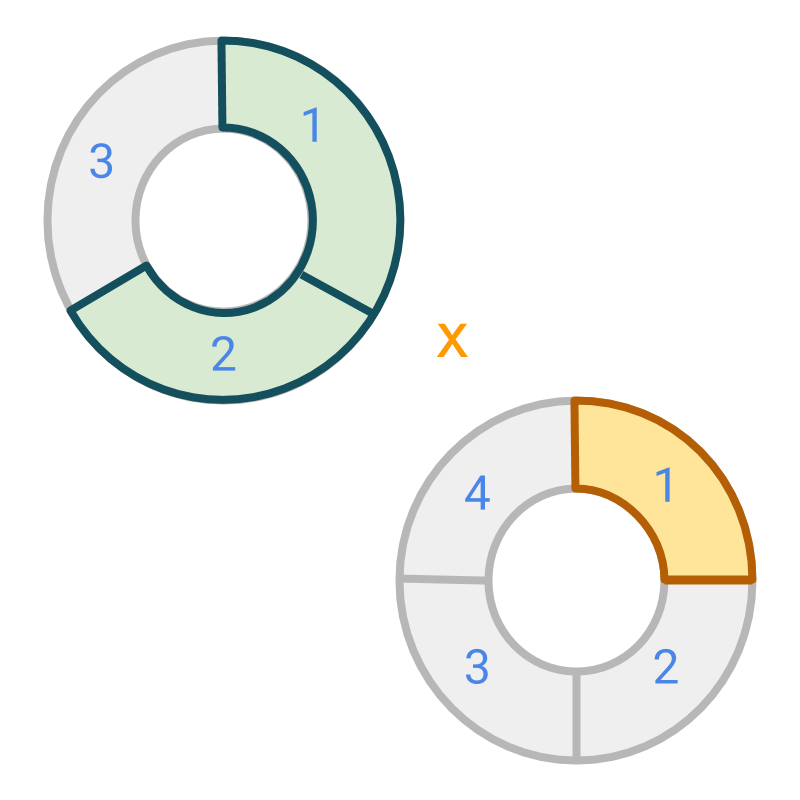
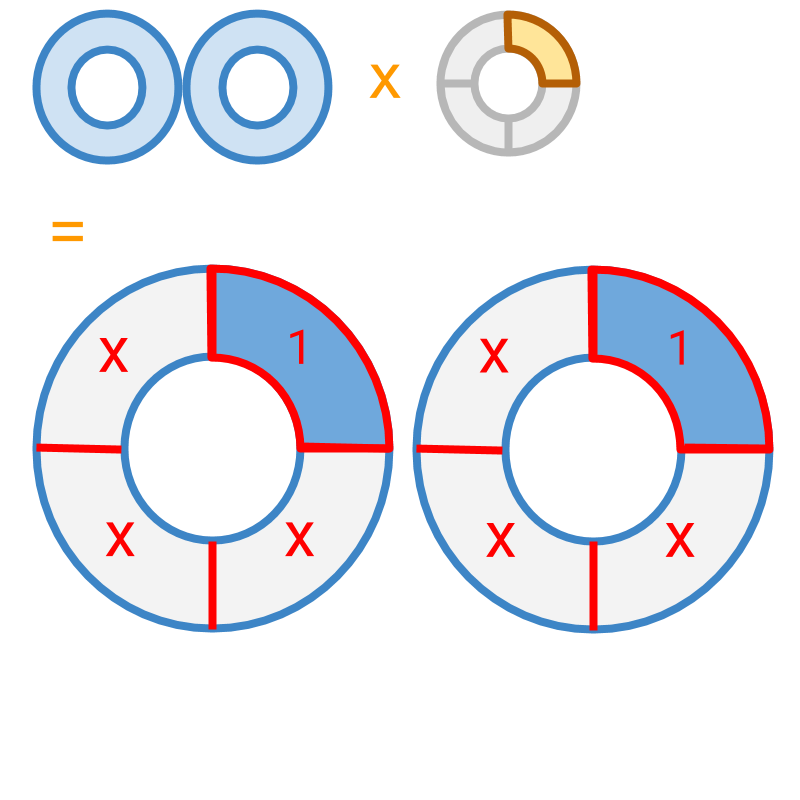
Multiplication by a fraction : consider $\frac{2}{3} \times \frac{1}{4}$ $2/3 xx 1/4$
Multiplicand $\frac{2}{3}$ $2/3$ is multiplied by a multiplier $\frac{1}{4}$ $1/4$ .
The multiplication process is illustrated in the next page.

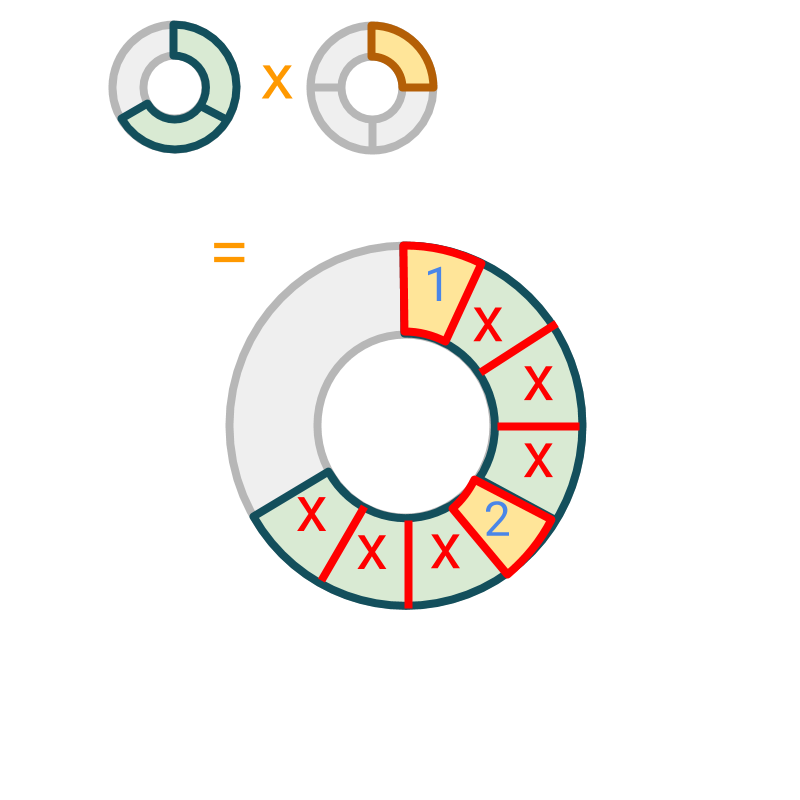
The multiplication $\frac{2}{3} \times \frac{1}{4}$ $2/3 xx 1/4$ is illustrated.

Each part of multiplicand is divided into $4$ $4$ parts (which is the place value of the multiplier) and product is found by selecting $1$ $1$ part (which is the numerator of the multiplier) from each.

The product is $2$ $2$ pieces in the place value $\frac{1}{12}$ $1/12$ which is $\frac{2}{12}$ $2/12$ .

$\frac{2}{12}$ $2/12$ can be simplified to $\frac{1}{6}$ $1/6$ .

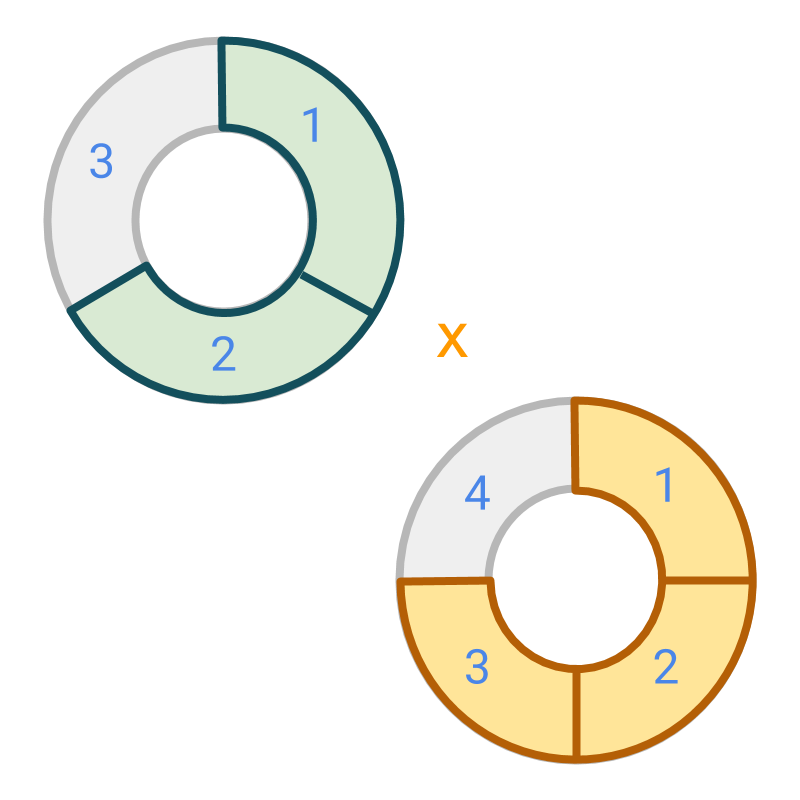
Multiplication by a fraction : Consider $\frac{2}{3} \times \frac{3}{4}$ $2/3 xx 3/4$
Multiplicand $\frac{2}{3}$ $2/3$ is multiplied by a multiplier $\frac{3}{4}$ $3/4$ .
The multiplication process is illustrated in the next page.

The multiplication $\frac{2}{3} \times \frac{3}{4}$ $2/3 xx 3/4$ is illustrated.

The each part of multiplicand is divided into $4$ $4$ parts (which is the place value of the multiplier) and product is found by selecting $3$ $3$ parts (which is the numerator of the multiplier) from each.

The product is $6$ $6$ pieces in the place value $\frac{1}{12}$ $1/12$ which is $\frac{6}{12}$ $6/12$ .

$\frac{6}{12}$ $6/12$ can be simplified to $\frac{1}{2}$ $1/2$ .

simplify

Having understood the first principles of multiplication of fractions, the procedural simplification for the same is :

• Numerators of multiplicand and multiplier are multiplied to numerator of product.

• Denominators of multiplicand and multiplier are multiplied to denominator of product.

Multiplication is understood in two steps

• The place value of multiplicand is modified by the place value of multiplier.

• The given number of multiplicand is multiplied by the given number of multiplier.

Multiplication of Fractions: For two fractions multiplicand $\frac{p}{q}$ $p/q$ and the multiplier $\frac{l}{m}$ $l/m$
Every $\frac{1}{q}$ $1/q$ part of multiplicand is split into $m$ $m$ pieces making it $\frac{1}{q \times m}$ $1/(q xx m)$ as the modified place value
) From each of $p$ $p$ parts of multiplicand $l$ $l$ parts make the product making $p \times l$ $p xx l$ parts
$p \times l$ $p xx l$ parts in $\frac{1}{q \times m}$ $1/(q xx m)$ place value gives the result $\frac{p \times l}{q \times m}$ $(p xx l)/(q xx m)$

example

Multiply $\frac{14}{18} \times \frac{3}{4}$ $14/18 xx 3/4$ .
The answer is ' $\frac{7}{12}$ $7/12$ '

summary

» $\frac{a}{b} \times \frac{c}{d}$ $a/b xx c/d$ $= \frac{a c}{b d}$ $= (ac)/(bd)$
» $2 \times \frac{1}{4}$ $color(deepskyblue)(2) xx color(coral)(1/4)$
    → $2$ $2$ pieces
    → $\frac{1}{4}$ $1/4$ of each of those pieces
    → result is count $2$ $2$ in place value $\frac{1}{4}$ $1/4$
    → $= \frac{2}{4}$ $= 2/4$

» $\frac{2}{3} \times \frac{3}{4}$ $color(darkgreen)(2/3) xx color(coral)(3/4)$
    → $2$ $color(darkgreen)(2)$ pieces in place value $\frac{1}{3}$ $color(darkgreen)(1/3)$
    → $\frac{3}{4}$ $color(coral)(3/4)$ of each of those pieces
    → result is count $6$ $6$ in place value $12$ $12$
    → $= \frac{6}{12} = \frac{1}{2}$ $= 6/12 = 1/2$

» Procedural Simplification: Multiply numerators and denominators. Cancel any common factors .
    → $\frac{2}{3} \times \frac{3}{4}$ $2/3 xx 3/4$
    → $\frac{2 \times 3}{3 \times 4}$ $(2 xx 3)/(3 xx4)$
    → common factors $3$ $3$ and $2$ $2$ canceled
    → $= \frac{1}{2}$ $= 1/2$

Outline

The outline of material to learn "fractions" is as follows.

• click here for detailed outline of Fractions

→ Part of whole

→ Dividing a group

→ Fractions as Directed numbers

→ Like and Unlike Fractions

→ Proper and Improper Fractions

→ Equivalent & Simplest form

→ Converting unlike and like Fractions

→ Simplest form of a Fraction

→ Comparing Fractions

→ Addition & Subtraction

→ Multiplication

→ Reciprocal

→ Division

→ Numerical Expressions with Fractions

→ PEMA / BOMA