Fractions : Fractions: Part of a whole

maths > fractions

Fractions: Part of a whole

what you'll learn...

overview

Students are familiar with whole numbers and the place-value system followed in whole numbers.

• Whole numbers are used to count or measure.

• Whole numbers use place-value system of units, tens, hundreds etc. eg: In $234$ $234$ , the digit $2$ $2$ has a place value of $200$ $200$ .

This introduces fractions as count or number of pieces as numerator and the place-value of the count as denominator.

whole numbers

There are $5$ $5$ flowers in the picture. $5$ $5$ is a whole number used to represent the count or number of objects.

Natural numbers or counting numbers are numbers $1, 2, 3, \dots$ $1, 2, 3, cdots$ . Early humans naturally used hands to count and the numbers they used are 1, 2, 3.

Whole numbers are numbers $0, 1, 2, \dots$ $0,1,2,cdots$ .

face and place value

The actual value of the digits $0$ $0$ to $9$ $9$ without taking the position into consideration is the face value.

For example, $2$ $2$ in numbers $23$ $23$ and $213$ $213$ has face-value $2$ $2$ .

The value represented by the digit in the position it has, is the place-value of the digit.

For example, $2$ $2$ in the numbers $23$ $23$ and $213$ $213$ has place values $20$ $20$ and $200$ $200$ respectively.

cut into pieces

Consider the number of pizzas shown in the picture. The picture represents one pizza.

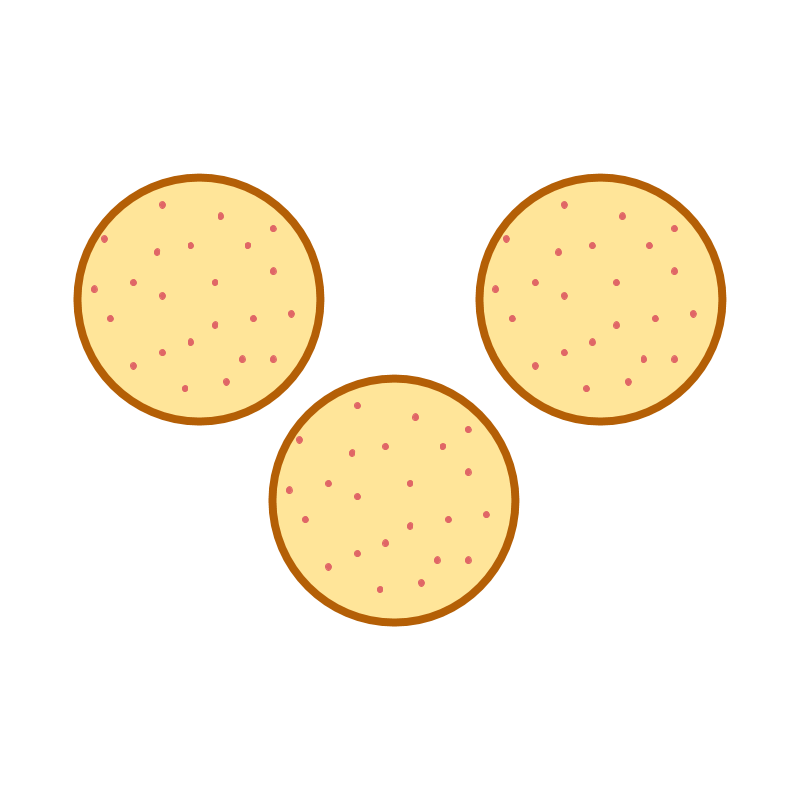
There are $3$ $3$ pizzas represented in this picture.

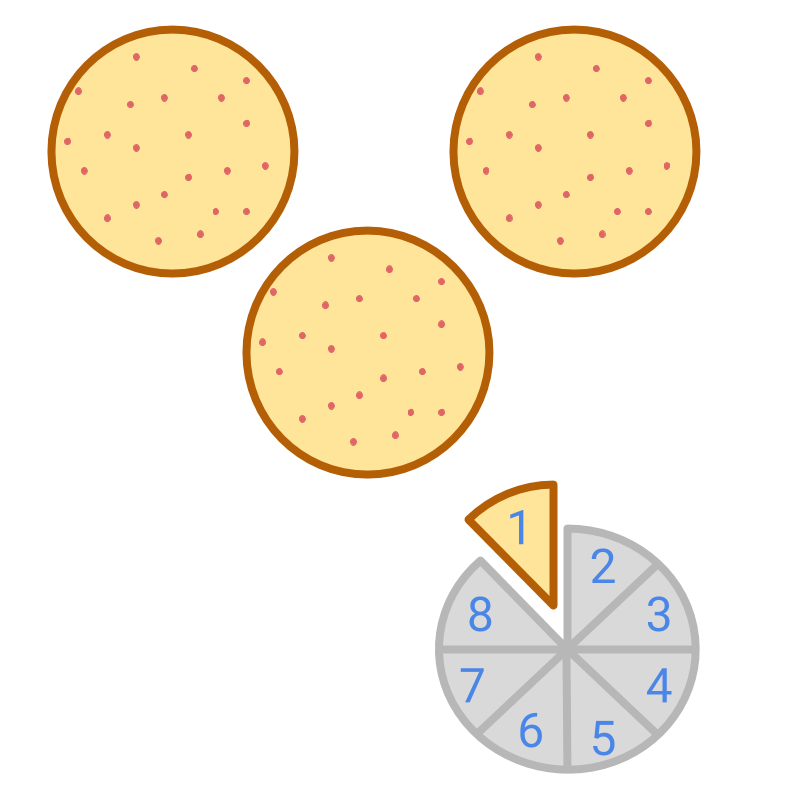
Consider the pizzas shown in the picture. It shows $3$ $3$ whole pizzas and $1$ $1$ piece.

The number of pizzas in the picture is half. Knowing that a pizza is circular, it is easily identified that the given piece is only half of the whole.

Consider the picture. The small portion is referred as one piece of the whole. Till now, whole number is used to count either the whole pizzas or the pieces.

The whole numbers can be used to count the pieces. Example: $2$ $2$ pieces, $5$ $5$ pieces, etc.

all pieces are not the same

Consider the two pieces of pizzas shown in the figure. The two pieces are not equal in size. It has to be counted as two unequal pieces of pizza. The interesting question is how to measure and specify these pieces.

How would one specify one piece from another piece?
It is known that the wholes are of equal sizes. So the piece can be specified with reference to the whole object.

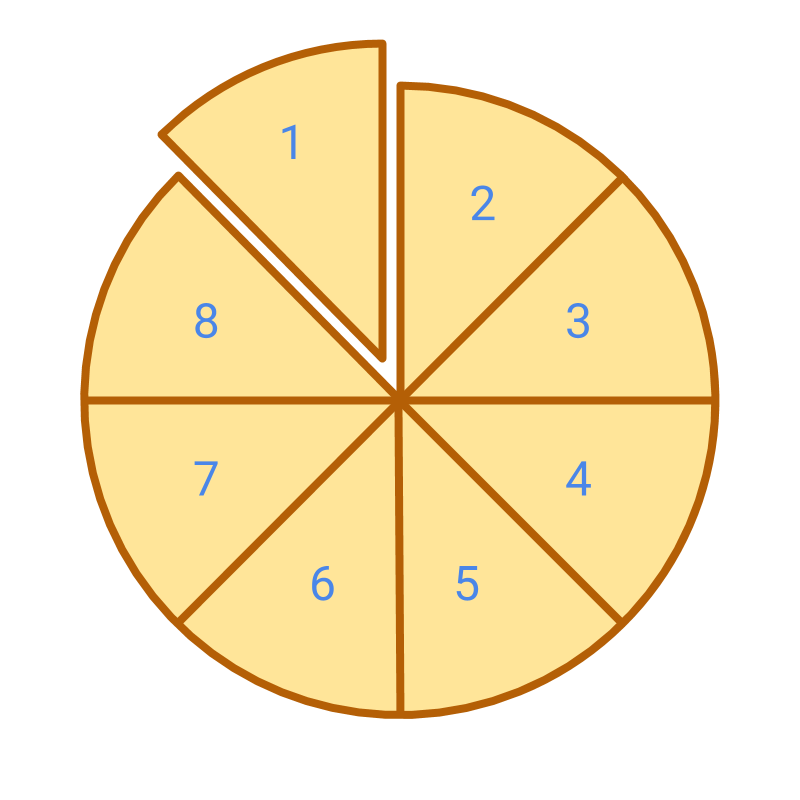
$fraction part of whole$

Consider the picture which shows the whole and one piece cut from the whole. The whole is cut into $8$ $8$ equal parts. $1$ $1$ part is considered. This is given as $1$ $1$ part in $8$ $8$ parts of the whole. This is represented by a fraction $\frac{1}{8}$ $1/8$

number of pieces with place value

$fraction illustration$

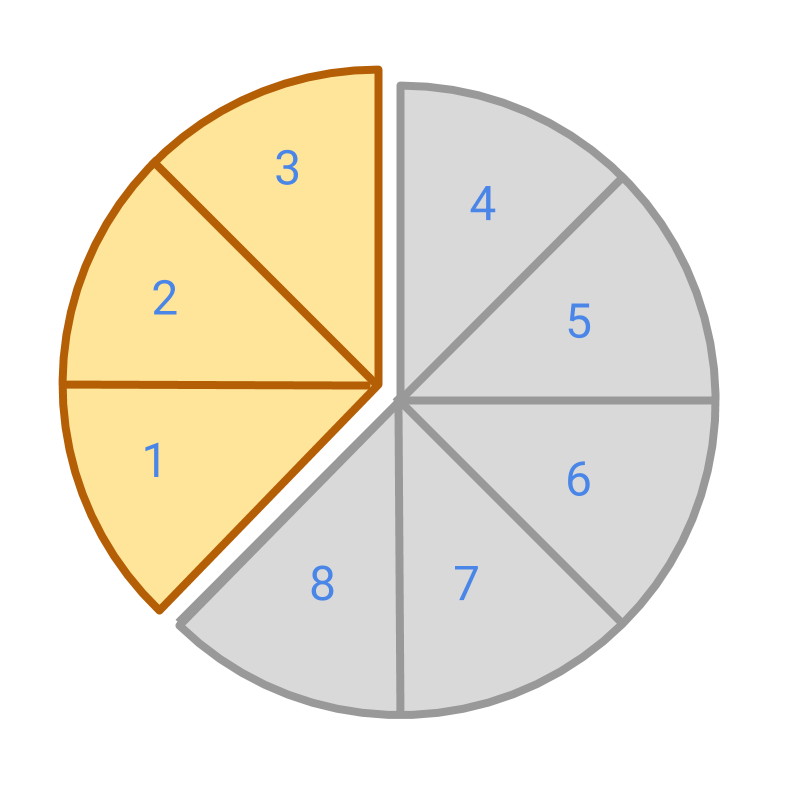
Consider the part shown in color. The whole is represented by a full circle. The whole is cut into $8$ $8$ equal parts. The colored portion represents $3$ $3$ parts in the $8$ $8$ parts of whole. The fraction is $\frac{3}{8}$ $3/8$

Consider the picture which shows the whole and one piece cut from the whole. In the fraction $\frac{3}{8}$ $3/8$ :

$3$ $3$ specifies the number of pieces considered, that is the face value of the fraction.

$8$ $8$ specifies the number of pieces that makes a whole. So, " $\frac{1}{8}$ $1/8$ " is the place value of the fraction.

Both face value and the place value, together form the fraction $\frac{3}{8}$ $3/8$ .

$fraction part of whole$

Consider the picture which shows the whole and one piece cut from the whole.
The whole is cut into $12$ $12$ equal parts. $1$ $1$ part is considered. This is given as $1$ $1$ part in $12$ $12$ parts of the whole. This is represented by a fraction $\frac{1}{12}$ $1/12$ .

In this, $1$ $1$ is the numerator of the fraction, and $12$ $12$ is the denominator of the fraction.

The word "numerator" means something that specifies a number. Numero is from root word counting. In fractions, numerator is the count of the part of the whole.

The English word denominator means something that specifies a standard. In fractions, the denominator is the place value of the part of the whole.

In a fraction $\frac{p}{q}$ $p/q$
the denominator specifies the standard divisions on the whole
the numerator provides the number or count of such divisions given by the fraction.

The picture specifies the fraction $\frac{3}{8}$ $3/8$ as
the total number of parts the whole is divided into : the denominator $8$ $8$
The number of parts that the fraction specifies : the numerator $3$ $3$ .

The English word fraction means: broken down or fractured into smaller parts.

$fraction illustration$

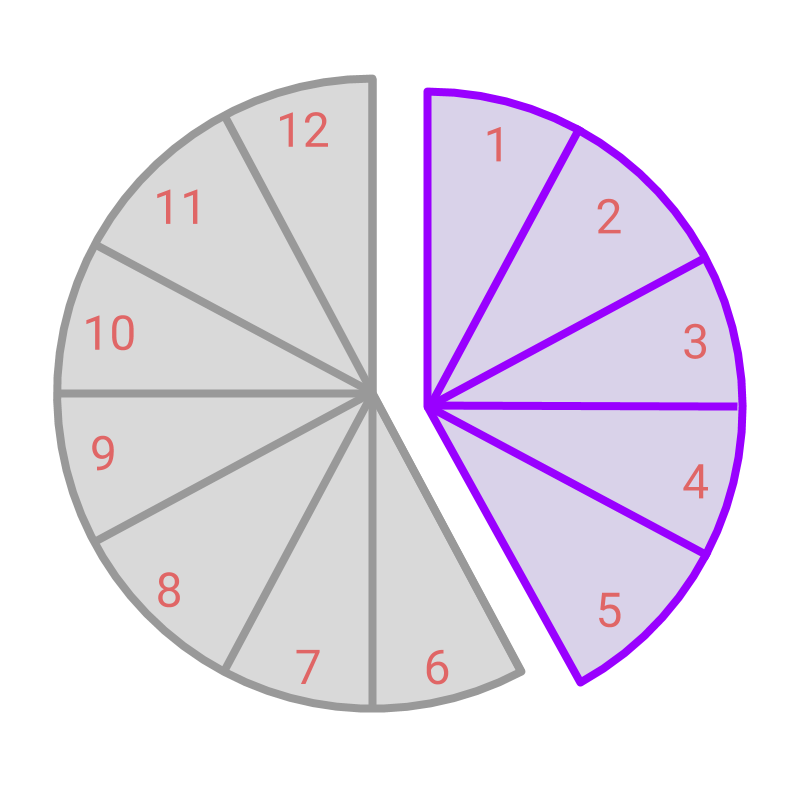
The whole is represented by a full circle. The whole is cut into $12$ $12$ equal parts. The colored portion represents $5$ $5$ parts in the $12$ $12$ parts of whole.

The fraction is $\frac{5}{12}$ $5/12$ .

part of whole

Numerator is the number of parts specified in a fraction.

Denominator is the number of parts that make a whole, and the place value of the given numerator.

Fraction is part of a whole, specified as numerator by denominator.

Fraction as part of whole: A fraction represents the number of parts out of the total number of parts in a whole.
Fraction is represented as $\frac{p}{q}$ $p/q$ , where $p$ $p$ and $q$ $q$ are integers and
$q$ $q$ is the denominator or the number of parts in a whole or the place value of $p$ $p$ .
$p$ $p$ is the numerator or the number of parts represented by the given fraction.

examples

$fraction illustration$

What is the fraction represented by the colored portion in the picture?
The answer is ' $\frac{1}{4}$ $1/4$ '.

$fraction illustration$

What is the fraction represented by the colored portion in the picture?
The answer is ' $\frac{4}{9}$ $4/9$ '.

summary

» Whole is split into parts » Fraction $\frac{5}{12}$ $5/12$
    → whole is divided into $12$ $12$ equal parts
    → $5$ $5$ parts is the given number
    → $\frac{1}{12}$ $1/12$ is the place value
» Fraction $\frac{5}{8}$ $5/8$
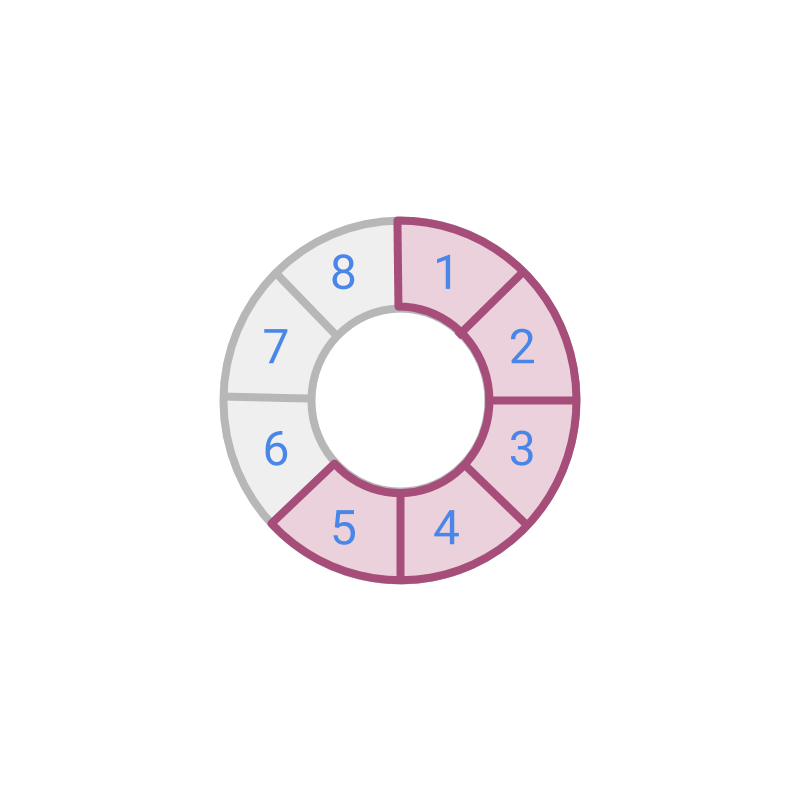    → whole is divided into $8$ $8$ equal parts
    → $5$ $5$ count is the given number
    → $\frac{1}{8}$ $1/8$ is the place value
» fraction in the form $\frac{p}{q}$ $p/q$
    → $p$ $p$ numerator (given number)
    → $q$ $q$ denominator (the place value or standard)
Consider the two numbers of fraction: numerator as the given number, and the denominator as the place value. That will make the fraction arithmetic easy to understand.

Outline

The outline of material to learn "fractions" is as follows.

• click here for detailed outline of Fractions

→ Part of whole

→ Dividing a group

→ Fractions as Directed numbers

→ Like and Unlike Fractions

→ Proper and Improper Fractions

→ Equivalent & Simplest form

→ Converting unlike and like Fractions

→ Simplest form of a Fraction

→ Comparing Fractions

→ Addition & Subtraction

→ Multiplication

→ Reciprocal

→ Division

→ Numerical Expressions with Fractions

→ PEMA / BOMA