Construction / Practical Geometry (basics) : Fundamentals of Construction : Triangles

maths > construction-basics

Fundamentals of Construction : Triangles

what you'll learn...

overview

This lesson gives a short overview of triangles. Three parameters define a triangle and the following possible combinations uniquely define a triangle

• Side-Side-Side (SSS)

• Side-Angle-Side (SAS)

• Angle-Side-Angle (ASA)

• right angle-hypotenuse-side (RHS)

• side-angle-altitude (SAL)

This set of parameters are given to construct a triangle.

A short analysis of constructing triangles with the following is provided.

• angle-angle-side (equivalent to angle-side-angle)

• angle-angle-angle (only 2 parameters)

• side-side-angle (two possible triangles)

• side-side-altitude (two possible triangles)

• rightangle-angle-side (equivalent to angle-side-angle)

Fundamentals of Construction : Triangles

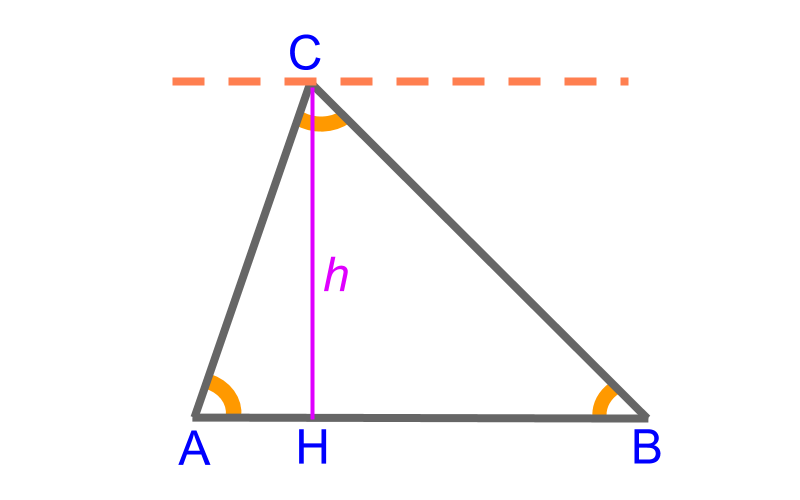
Triangle $△ A B C$ $/_\ ABC$ has the following measurements as the parameters

• side $¯ ¯¯¯¯ ¯ A B$ $bar(AB)$

• side $¯ ¯¯¯¯ ¯ B C$ $bar(BC)$

• side $¯ ¯¯¯¯ ¯ C A$ $bar(CA)$

• angle $∠ A$ $/_A$

• angle $∠ B$ $/_B$

• angle $∠ C$ $/_C$

• altitude or height of triangle $bar(CH) = l$

These are $7$ parameters in total. Among these $7$ , any $3$ independent parameters define a triangle. Other parameters can be derived from the given three parameters.

Note that the three angles are not truly independent as $/_A + /_B + /_C = 180^@$

Considering that triangles are defined by three independent parameters, one of the following possible combination is provided to construct a particular triangle.

• Side-Side-Side

• Side-Angle-Side

• Angle-Side-Angle

• right angle-hypotenuse-side

• side-angle-altitude

angle-angle-angle is just two independent parameters as the sum of angles are $180^@$ .

side-angle-angle is same as angle-side-angle, as the sum of interior angles property defines the third angle.

side-side-angle is ambiguous with two possible triangles, unless the given angle is $90^@$ or obtuse

side-side-altitude is ambiguous with two possible triangles, unless it is right-triangle

The given parameters have to satisfy properties of a triangle.

eg1: $4,4,10$ cm cannot be sss of a triangle, as sum of any two sides of a triangle has to be greater than the third side.

eg2: $200^@$ cannot be an interior angle of a triangle, as sum of angles has to be $180^@$

Defining a Triangle : Three parameters define a triangle and the following possible combinations uniquely define a triangle

• Side-Side-Side (SSS)

• Side-Angle-Side (SAS)

• Angle-Side-Angle (ASA)

• right angle-hypotenuse-side (RHS)

• side-angle-altitude (SAL)

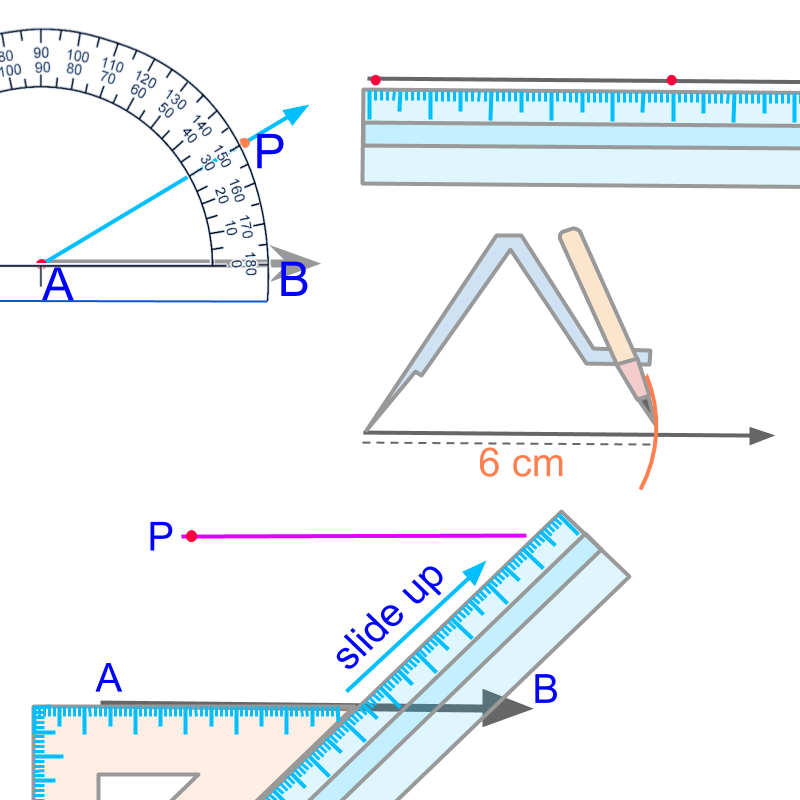
4 fundamental elements of practical geometry

In practical geometry, we study construction of various figures using a scale, protractor, compass, and set-squares. Using these instruments, some fundamental elements of construction are realized.

The fundamental elements of practical geometry are

   constructing a line (collinear points),

   Constructing an arc (equidistant points),

   Constructing an angle or (equiangular points), and

   Constructing a parallel (parallel points)

To construct any shape, the fundamental elements we use are

• Construct a line passing through the two given points using a ruler or scale (collinear points)

• Construct a ray at the given angle using a protractor (equiangular points)

• Construct an arc at the given distance using a compass and a ruler or scale (equidistant points)

• construct a parallel line using a set-square and a scale or another set-square. (points on a parallel)

sss

To construct a triangle, "side-side-side" is provided. The construction of the specified triangle is accomplished with
• a scale to measure and
• a compass to mark the given sides

To construct a triangle $/_\ ABC$ with given "side-side-side" $7$ cm, $4$ cm, and $5$ cm $• Construct a line and mark side$ bar(AB) $with a compass measuring$ 7 $cm • measure$ bar(AC)4 $cm in a compass and draw an arc • measure$ bar(BC)5 $cm in a compass and draw an arc • the two arcs cut at point$ C $. Connect the points for sides$ bar(AC) $and$ bar(BC)/_\ ABC` is constructed.

Construction of SSS triangle : Use compass to measure lengths and mark points at the given three distances.

sas

To construct a triangle, "side-angle-side" is provided. The construction of the specified triangle is accomplished with
• a protractor to measure the angle
• a scale to measure and
• a compass to mark the given sides

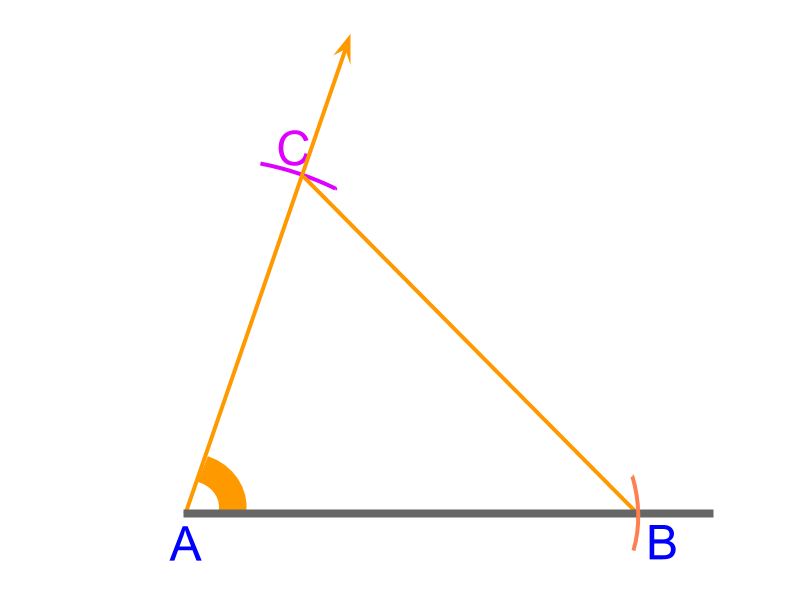
To construct a triangle $/_\ ABC$ with given "side-angle-side" $4$ cm, $70^@$ , and $6$ cm.

• Construct a line and mark side $bar(AB)$ with a compass measuring $6$ cm

• measure $70^@$ angle and draw a ray from point $A$

• measure $bar(AC)$ $4$ cm in a compass and draw an arc cutting the ray

• the arc and the ray cut at point $C$ . Connect the point to point $B$ to get $bar(BC)$

$/_\ ABC$ is constructed.

Construction of SAS triangle : Use compass to the measure lengths and protractor to measure the given angle. Once the vertices are marked, join them to form the triangle.

asa

To construct a triangle, "angle-side-angle" is provided. The construction of the specified triangle is accomplished with
• a protractor to measure the angles
• a scale to measure the side and
• a compass to mark the side

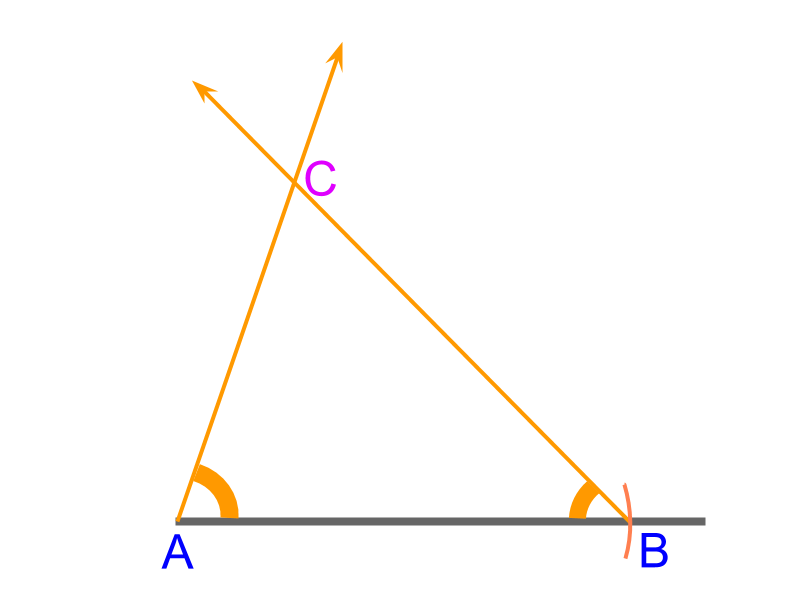
To construct a triangle $/_\ ABC$ with given "angle-side-angle" $70^@$ , $6$ cm, and $50^@$

• Construct a line and mark side $bar(AB)$ with a compass measuring $6$ cm

• measure $70^@$ angle and draw a ray from point $A$

• measure $50^@$ angle and draw a ray from point $B$

• the two rays cut at point $C$ .

$/_\ ABC$ is constructed.

Construction of ASA triangle : Use compass to measure lengths and protractor to measure given angle. Once the vertices are marked, join them to form the triangle.

rhs

To construct a triangle, "right angle-side-hypotenuse" is provided. "angle-side-side" is equivalent to the given information.

Note: The third side of a right triangle can be calculated using Pythagorean theorem. But, in construction problems, the objective is to construct without complex geometrical calculations involving square-root.

Note the order of the given parameters matters. For example, $3cm-60^@-4cm$ is different from $60^@-3cm-4cm$ .

To construct a triangle $/_\ ABC$ with given "right angle-side-hypotenuse" $4$ cm and $5$ cm

• Construct a line and mark side $bar(AB)$ with a compass measuring $4$ cm

• measure $90^@$ angle and draw a ray from point $A$

• measure $bar(BC)$ $5$ cm in a compass and draw an arc from point $B$ cutting the ray

• the arc and the ray cut at point $C$ . Connect the point to point $B$ to get $bar(BC)$

$/_\ ABC$ is constructed.

There are few things to note in construction of "rhs".

Note 1: The method is called either as "rhs" or "rsh".

Note 2: In other formats, the order of the given parameters matter. For example in "sas", the given angle is subtended by the given two sides. In "rhs" the there parameters are not given in order, but are connected by the properties of right-triangles. Among the two given sides, the longer one is the hypotenuse.

Note 3: If the angle is not right-angle, then "angle-side-side" may (under some conditions) lead to two possible triangles. This is explained later.

Construction of RHS triangle : Use compass to the measure lengths and protractor to measure the given angle. Once the vertices are marked, join them to form the triangle.

sal

To construct a triangle, "side-angle-altitude" are provided. The construction of the specified triangle is accomplished with
• a protractor to measure the angle
• a scale and compass to measure mark the side,
• a set-squares to mark a parallel at the altitude.

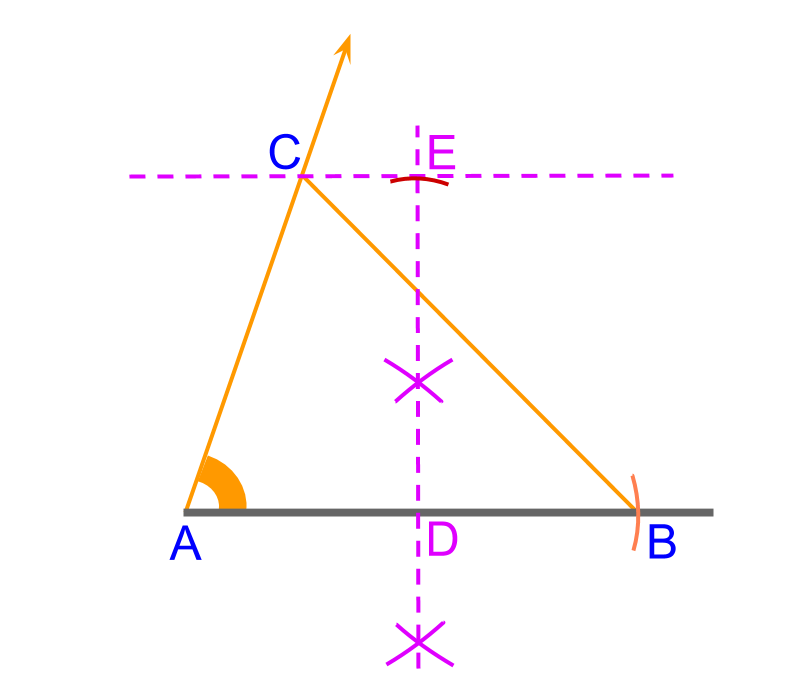
To construct a triangle $/_\ ABC$ with given "side-angle-altitude" $4$ cm, $70^@$ , and $5$ cm.

• Construct a line and mark side $bar(AB)$ with a compass measuring $6$ cm

• measure $70^@$ angle and draw a ray from point $A$

• The objective is to draw a parallel at given $5$ cm distance. To achieve this, draw a perpendicular bi-sector for $bar(AB)$ and from point $D$ mark point $E$ at $5$ cm. Construct a parallel to on $bar(AB)$ point $E$

• the parallel and the ray cut at point $C$ . Connect the point to point $B$ to get $bar(BC)$

$/_\ ABC$ is constructed.

Construction of SAL triangle : Use a ruler, protractor, a compass, and a set-square to mark side, angle and parallel. Once the vertices are marked, join them to form the triangle.

aas

To construct a triangle, "angle-angle-side" is provided. This is equivalently "angle-side-angle" as the sum of angle is $180^@$ . The construction of the specified triangle is accomplished by converting it into asa form.

aaa

To construct a triangle, "angle-angle-angle" is provided.

It is noted that, the given angles are not $3$ independent parameters as with $2$ angles the third angle is defined. The $3$ angles together form $2$ independent parameters.

ssa

To construct a triangle, "side-side-angle" is provided. It is noted that the given information "side-side-angle" may lead to two possible solutions.

To construct a triangle, "side1-side2-angle" are provided. The top portion of the figure illustrates the construction.

• Side2 $bar(AB)$ is constructed

• $/_A$ is constructed with $vec(AP)$ .

• side1 is to be constructed. With a compass from point $B$ , an arc is drawn. This cuts at 2 points $C1$ and $C2$ . The triangles $/_\ ABC1$ and $/_\ ABC2$ both satisfy the given parameters

   $bar(AB)$ is the given side2

   $/_A$ is the given angle

   Both $bar(BC1)$ and $bar(BC2)$ equal side1.

Since this leads to two possible solutions, the triangle is not uniquely defined.

Under some conditions, the given information "side1-side2-angle" leads to an unique triangle. This is illustrated in the lower part of the figure.

• when the given angle is obtuse, the side1 has to be greater than side2. This is illustrated in $/_\ ABC3$ .

• when the side1 is greater than the side2. This is illustrated in $/_\ ABC4$

ssl

To construct a triangle, "side-side-altitude" are provided. It is noted that the given information "side-side-altitude" may lead to two possible solutions

To construct a triangle, "side1-side2-altitude" is provided. The figure illustrates possible construction.

• Side2 $bar(AB)$ is constructed

• Parallel at altitude is constructed at point $E$ .

• Side1 is to be constructed. With a compass from point $A$ , an arc is drawn. This cuts at 2 points $C1$ and $C2$ .

The triangle $/_\ ABC1$ and $/_\ ABC2$ both satisfy the given parameters

   $bar(AB)$ is the given side2

   $bar(DE)$ is the given altitude

   Both $bar(AC1)$ and $bar(AC2)$ equal side1.

Since this leads to two possible solutions, the given S A L does not uniquely define a triangle.

ras

To construct a triangle, "right angle-angle1-side" are provided. This is accomplished by converting to $right angle-side-angle2$ by sum of interior angle property.

rah

To construct a triangle, "right angle-angle1-hypotenuse" is provided. This is accomplished by converting to $angle1-hypotenuse-angle2$ by sum of interior angle property.

summary

The following four fundamental elements of construction are realized using a scale, protractor, compass, and set-squares

   constructing a line (collinear points),

   Constructing an arc (equidistant points),

   Constructing an angle or (equiangular points), and

   Constructing a parallel (parallel points)

Construction of Triangles : Three parameters define a triangle and the following possible combinations uniquely define a triangle

• Side-Side-Side (SSS)

• Side-Angle-Side (SAS)

• Angle-Side-Angle (ASA)

• right angle-hypotenuse-side (RHS)

• side-angle-altitude (SAL)

The geometrical instruments are used to construct the triangles of given parameters.s

Outline