Construction / Practical Geometry (basics) : Perpendicular Bisector to a Line Segment

maths > construction-basics

Perpendicular Bisector to a Line Segment

what you'll learn...

overview

In this page, the following are explained.

• constructing a bisector to a line segment

• constructing a perpendicular through a point on a line

• constructing a perpendicular to a point not on a line

• constructing a bisector to a given angle

Perpendicular Bisector to a Line Segment

A rhombus is "A four sided figure with all sides equal".

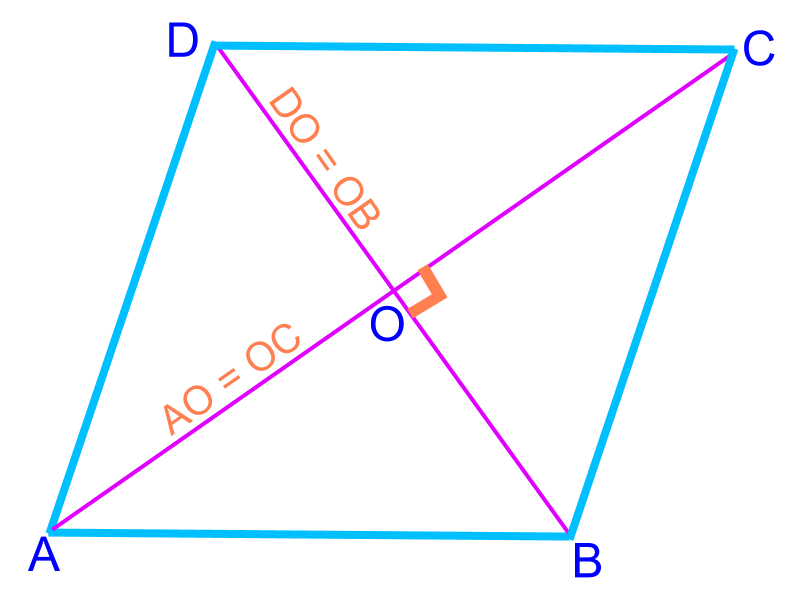
A rhombus has the following properties.

• All sides are equal (and parallel)

• the diagonals perpendicularly bisect

• opposite angles are equal

• adjacent angles are supplementary

"Diagonals of rhombus perpendicularly bisect" This geometrical properties help to construct a perpendicular bisector to a line.

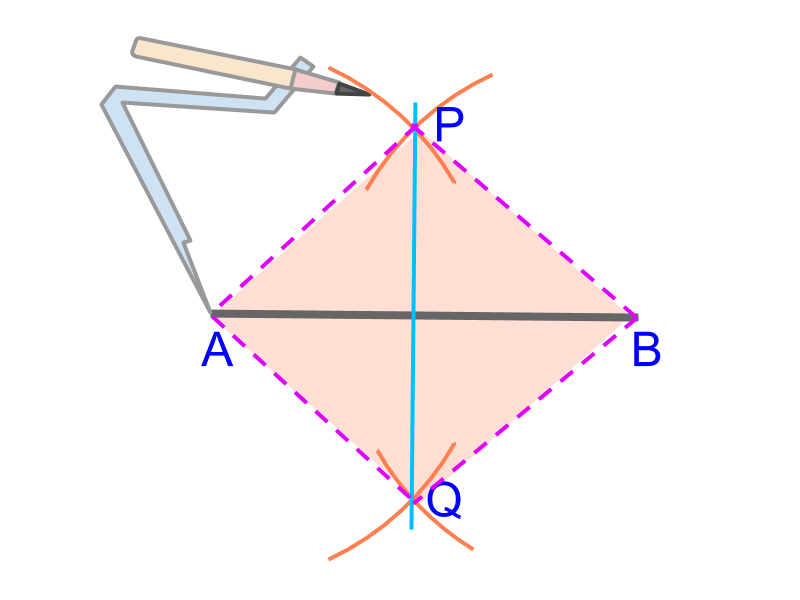
Given line segment $¯ ¯¯¯¯ ¯ A B$ $bar(AB)$ . The perpendicular bisector $¯ ¯¯ ¯ p q$ $bar(pq)$ is to be constructed.

• Take a compass

• fix a random distance between tips

• construct arcs from position $A$ $A$ above and below $¯ ¯¯¯¯ ¯ A B$ $bar(AB)$

• construct arcs from position $B$ $B$ above and below $¯ ¯¯¯¯ ¯ A B$ $bar(AB)$

• the intersecting points are $P$ $P$ and $Q$ .

Note that the distance between tips of the compass is not modified and so, the sides $bar(AP)$ , $bar(PB)$ , $bar(BQ)$ , and $bar(QA)$ form a rhombus. From the property of a rhombus, the diagonals $bar(AB)$ and $bar(PQ)$ perpendicularly bisect each other.

Note for curious students: It can be a kite, with $bar(AB)$ as minor diagonal. Property of a kite, the major diagonal $bar(PQ)$ bisects minor diagonal $bar(AB)$ .

Bisecting a Line Segment : Use a compass to mark a rhombus with the given line segment as one of the diagonals. The perpendicular bisector is the other diagonal.

Perpendicular through a point on a line

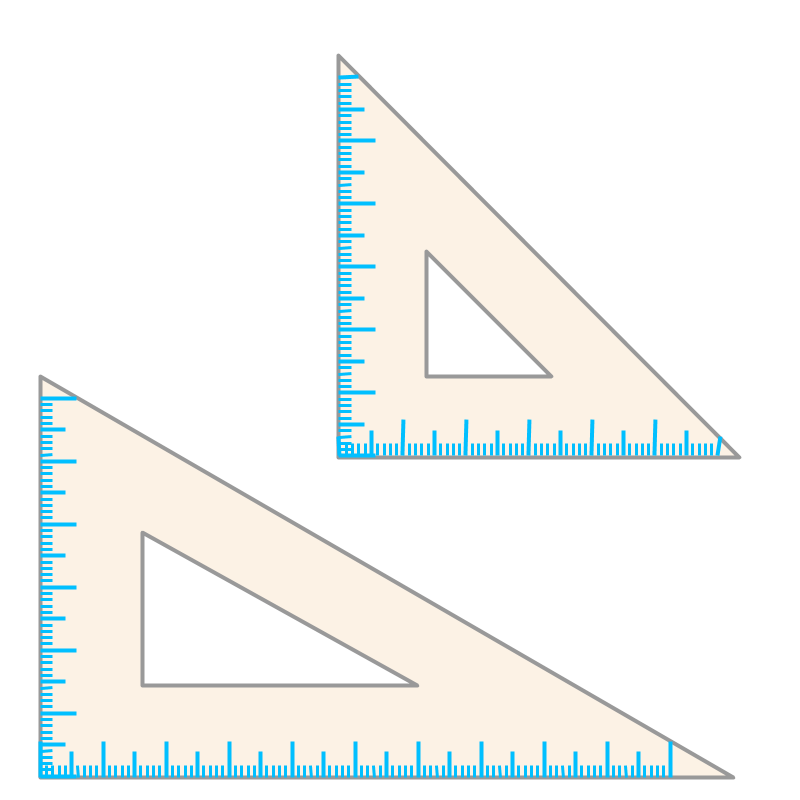
Set squares or set triangles have sides or edges that are perpendicular.

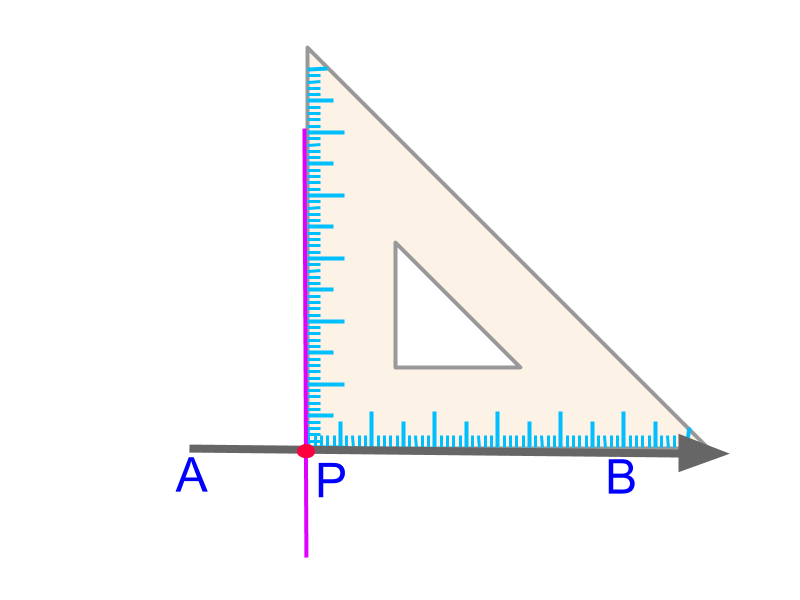
Given line $bar(AB)$ and a point $P$ on the line. Place the vertex of perpendicular edges of a set-square with one edge on the given line $bar(AB)$ . Construct the line along the other perpendicular edge of the set-square.

Perpendicular through a point on a line : Use the perpendicular edges of a set square, one edge on the given line and the perpendicular-vertex on the given point. Construct a line along the other perpendicular edge.

Some alternate methods can be used to construct a perpendicular through a point on a line.

• method to construct perpendicular bisector using a compass

• method to measure $90^@$ angle using a protractor

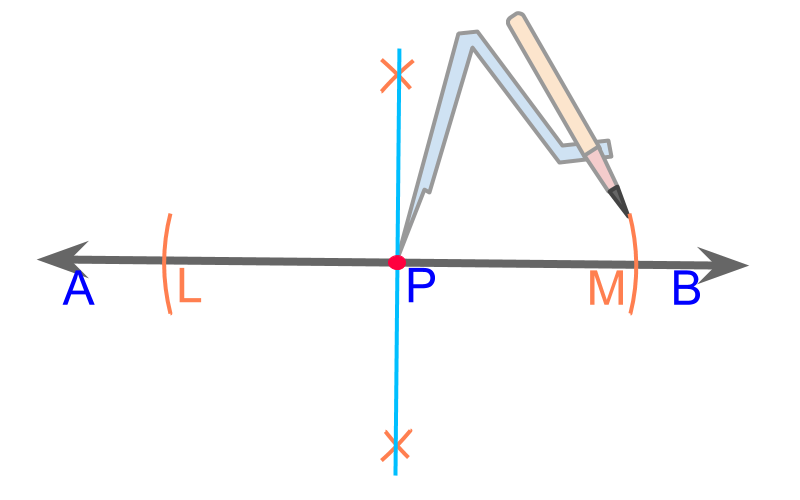
Perpendicular through a point on a line : Use a compass to mark points $L$ and $M$ on the line that are in equal distance from the given point $P$ . Construct the perpendicular bisector of $bar(LM)$ .

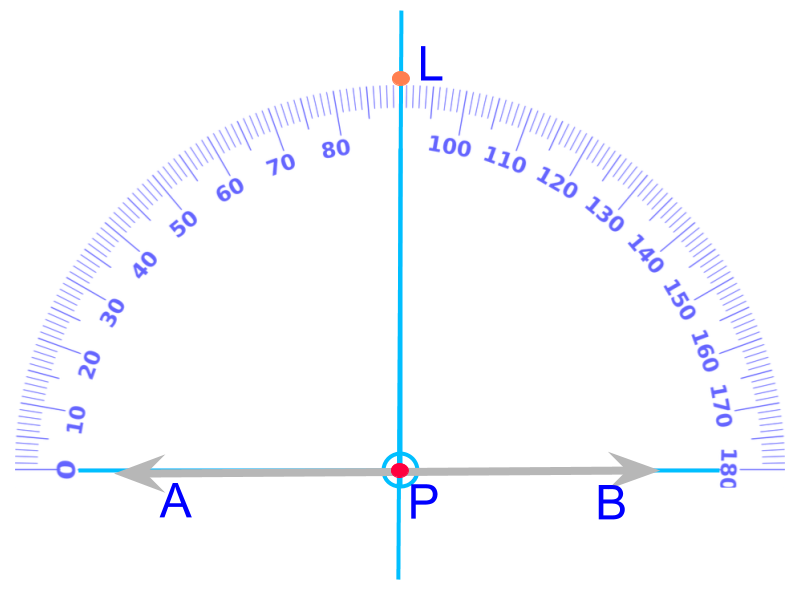
Perpendicular through a point on a line : Place the protractor with origin on the given point and the base-line on the given line. Mark a point on $90^@$ angle and draw a line through the given point and the marked point.

Perpendicular to a point not on a line

Set squares can help to construct a perpendicular to a line through a point outside the line.

Perpendicular to a Point : Use the perpendicular edges of a set square, one edge on the given line and the other edge on the given point. Construct a line along the other perpendicular edge.

Perpendicular to a Point : Use a compass to mark points $L$ and $M$ on the line that are in equal distance from the given point $P$ . Construct the perpendicular bisector of $bar(LM)$ .

Bisecting an angle

A kite is a quadrilateral with two pair of equal and adjacent sides.

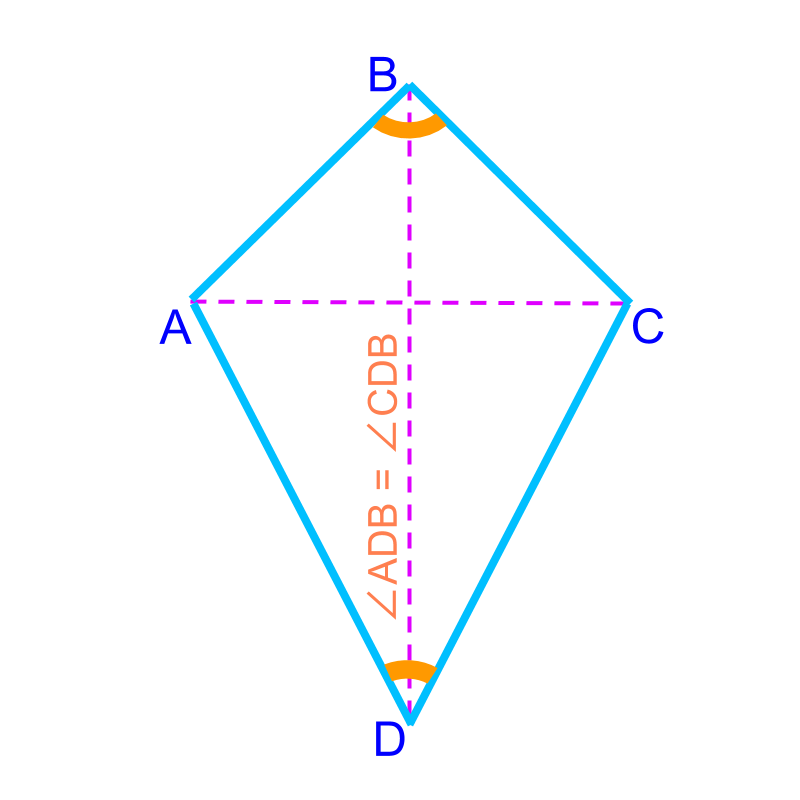
A kite has the following properties

• two pair of equal sides

• major diagonal perpendicularly bisects the minor diagonal. the diagonal that divides the kite into two congruent triangles is called major. The other diagonal is the minor diagonal.

• major diagonal bisects the angles at the vertices

• two equal opposite angles and two unequal opposite angles -- all sum up to $360^@$

The geometrical property "major diagonal of a kite bisect the angles at both vertices" can be used to bisect a given angle.

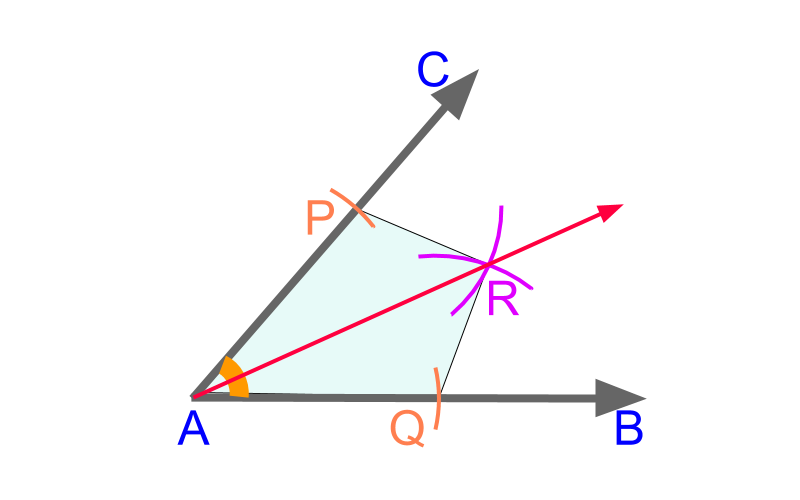
Given angle $/_BAC$ , a kite $AQRP$ is formed.

• With an arbitrary measure on compass, mark points $P$ and $Q$ from the point $A$ .

• With another arbitrary measure on compass, construct arcs from points $P$ and $Q$ . These two arcs cut at point $R$ .

The quadrilateral $AQRP$ is a kite and the line $bar(AR)$ is the major bisector of angle $/_BAC$ .

Bisecting an Angle : Using the two rays of the angle, create a kite such that the major diagonal bisects the angle.

summary

Bisecting a Line Segment : Use a compass to mark a rhombus with the given line segment as one of the diagonals. The perpendicular bisector is the other diagonal.

Perpendicular through a point on a line : Use the perpendicular edges of a set square, one edge on the given line and the perpendicular-vertex on the given point. Construct a line along the other perpendicular edge.

Perpendicular through a point on a line : Use a compass to mark two points on the line that are in equal distance from the given point. Construct the perpendicular bisector between the two marked points.

Perpendicular through a point on a line : Place the protractor with origin on the given point and the base-line on the given line. Mark a point on $90^@$ angle and draw a line through the given point and the marked point.

Perpendicular to a Point : Use the perpendicular edges of a set square, one edge on the given line and the other edge on the given point. Construct a line along the other perpendicular edge.

Perpendicular to a Point : Use a compass to mark points two points on the line that are in equal distance from the given point. Construct the perpendicular bisector between the two marked points.

Bisecting an Angle : Using the two rays of the angle, create a kite such that the major diagonal bisects the angle.

Outline