Construction / Practical Geometry (basics) : Fundamentals of Construction : Quadrilaterals

maths > construction-basics

Fundamentals of Construction : Quadrilaterals

what you'll learn...

overview

In this page, an overview of approaching construction problems for various quadrilateral forms is provided.

• A quadrilateral form has some additional properties, for example: all sides of a square are equal and the four angles are $90^{\circ}$ $90^@$ .

• A quadrilateral is seen to be combination of two triangles.

Using the properties, the construction is simplified into combination of triangles of sss, sas, asa, rhs, sal.

recap

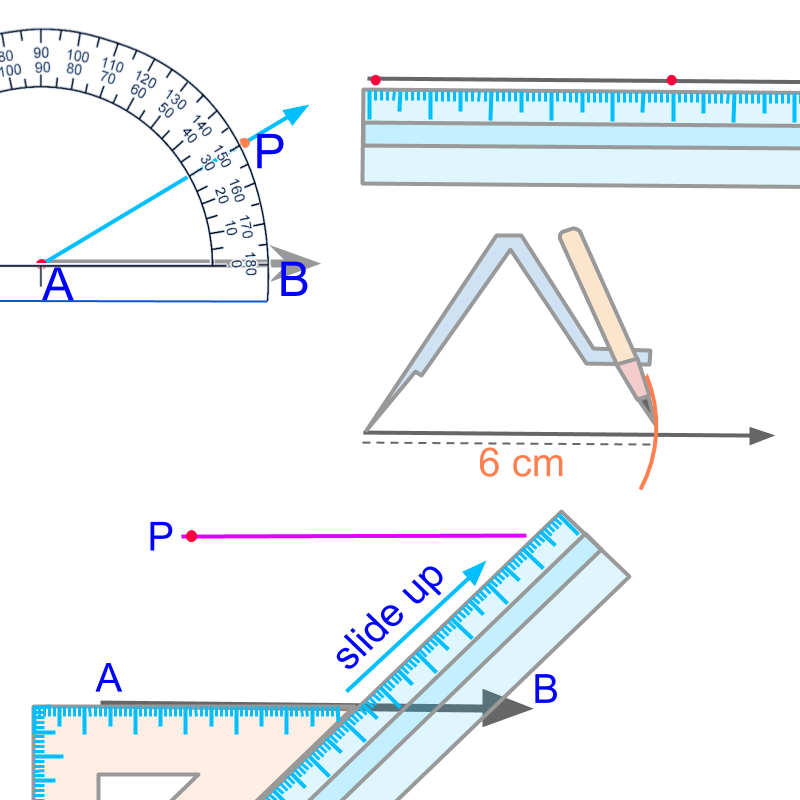
4 fundamental elements of practical geometry

In practical geometry, we study construction of various figures using a scale, protractor, compass, and set-squares. Using these instruments, the following fundamental elements of construction are realized.

   constructing a line (collinear points),

   Constructing an arc (equidistant points),

   Constructing an angle or (equiangular points), and

   Constructing a parallel (parallel points)

To construct any shape, the fundamental elements we use are

• Construct a line passing through the two given points using a ruler or scale (collinear points)

• Construct a ray at the given angle using a protractor (equiangular points)

• Construct an arc at the given distance using a compass and a ruler or scale (equidistant points)

• construct a parallel line using a set-square and a scale or another set-square. (points on a parallel)

Fundamentals of Construction : Triangles

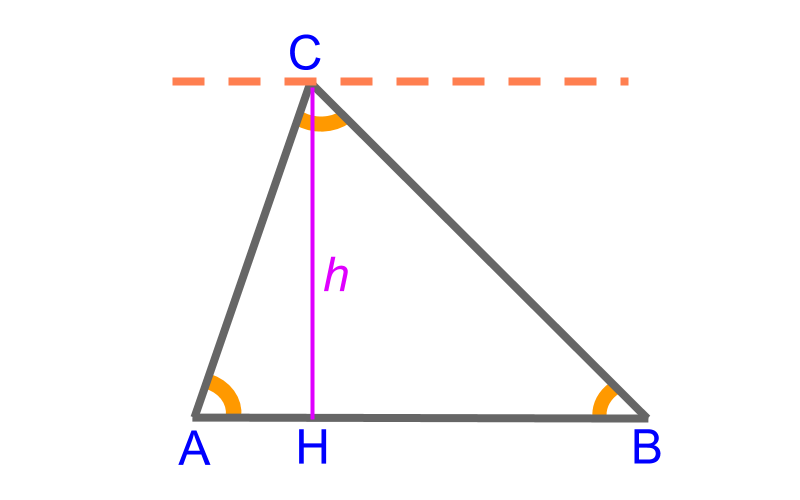
Triangle $△ A B C$ $/_\ ABC$ has the following measurements as the parameters

• side $¯ ¯¯¯¯ ¯ A B$ $bar(AB)$

• side $¯ ¯¯¯¯ ¯ B C$ $bar(BC)$

• side $¯ ¯¯¯¯ ¯ C A$ $bar(CA)$

• angle $∠ A$ $/_A$

• angle $/_B$

• angle $/_C$

• altitude or height of triangle $bar(CH) = l$

These are $7$ parameters in total. Among these $7$ , any $3$ independent parameters define a triangle. Other parameters can be derived from the given three parameters.

Note that the three angles are not truly independent as $/_A + /_B + /_C = 180^@$

Considering that triangles are defined by three independent parameters, one of the following possible combination is provided to construct a triangle.

• Side-Side-Side

• Side-Angle-Side

• Angle-Side-Angle

• right angle-side-hypotenuse

• angle-side-altitude

angle-angle-angle is just two independent parameters as the sum of angles are $180^@$ .

side-angle-angle is same as angle-side-angle, as the sum of angle property defines the third angle.

The given parameters have to satisfy properties of a triangle.

eg1: $4,4,10$ cm cannot be sss of a triangle, as sum of any two sides of a triangle has to be greater than the third side.

eg2: $200^@$ cannot be an interior angle of a triangle, as sum of angles has to be $180^@$

To construct a triangle, "angle-angle-side" is provided.

This is equivalently "angle-side-angle" as the sum of angle is $180^@$ . The construction of the specified triangle is accomplished by converting it into asa form.

To construct triangles, sometimes the properties of triangles are used. Similarly, to construct quadrilaterals, the properties of the quadrilaterals are used.

Quadrilaterals are plane figures of $4$ sides.

Types of Quadrilaterals

• Irregular Quadrilateral

• Parallelogram

• Rhombus

• Rectangle

• Square

• Trapezium

• Kite

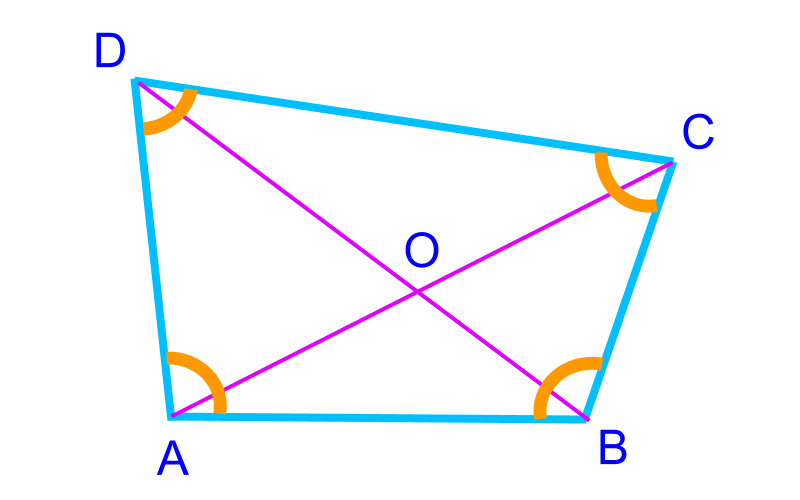
The possible parameters defining a quadrilateral are

• the four sides $bar(AB)$ , $bar(BC)$ , $bar(CD)$ , and $bar(AD)$

• the four angles $/_A$ , $/_B$ , $/_C$ , and $/_D$

• the two diagonals $bar(AC)$ and $bar(BD)$

Among these $10$ , any $5$ independent parameters define a quadrilateral.

Note that the four angles are not truly independent as sum of all four angles are $180^@$

Consider the quadrilateral as four vertices. The four vertices make two triangles. Quadrilateral is considered to be made of two triangles. Three vertices form the first triangle. The fourth vertex is placed in reference to the first triangle and thus, the fourth vertex and two more vertices of the first triangle form the second triangle.

• $/_\ ABC$ and $/_\ ACD$ define the four vertices

• $/_\ ABC$ and $/_\ ABD$ define the four vertices

• $/_\ ABC$ and $/_\ BCD$ define the four vertices.

A triangle is defined by $3$ parameters and A quadrilateral is defined by $5$ parameters.

The five parameters defining the quadrilateral are considered as two triangles and the various methods of constructing triangles are employed.

• Construction of Triangle SSS

• Construction of Triangle SAS

• Construction of Triangle ASA

• Construction of Triangle RHS

• Construction of Triangle SAL

Construction of quadrilateral has very many possible formulations. No need to memorize or learn by rote.

Always look for triangles, that is, one point is defined in reference to another two points by one of $SSS$ , $SAS$ , $ASA$ , $RHS$ , or $SAL$ methods.

Look for properties of specific type of quadrilaterals to figure out more information.

This is the most important learning in this topic. Once you work out the first problem in this formulation, the rest of the problems will become very very easy.

summary

Construction of Quadrilateral : The $4$ vertices of quadrilateral are defined by $5$ parameters. The $5$ parameters are considered as two triangles.

Once the two triangles are identified, use the SSS / SAS / ASA / RHS / SAL methods to construct the vertices of the two triangles and thus, the quadrilateral.

Outline