Construction / Practical Geometry (basics) : Construction of Quadrilaterals

maths > construction-basics

Construction of Quadrilaterals

what you'll learn...

overview

In this page, constructing quadrilaterals is explained. It is outlined as follows.

• Properties of quadrilaterals is explained

• The number of independent parameters in a quadrilateral is $1$ $1$

• For a given parameter, construction of quadrilaterals is approached as combination of triangles (sss, sas, asa, rhs, sal) and using the properties of quadrilaterals.

recap

In a quadrilateral,

• sum of all interior angles is $360^{\circ}$ $360^@$ . A quadrilateral is made of two triangles sharing one side. Each triangle is defined by $3$ $3$ parameters and since they share a side, one parameter is common in the two sets of $3$ $3$ parameters. Thus, a quadrilateral is defined by $5$ $5$ parameters.

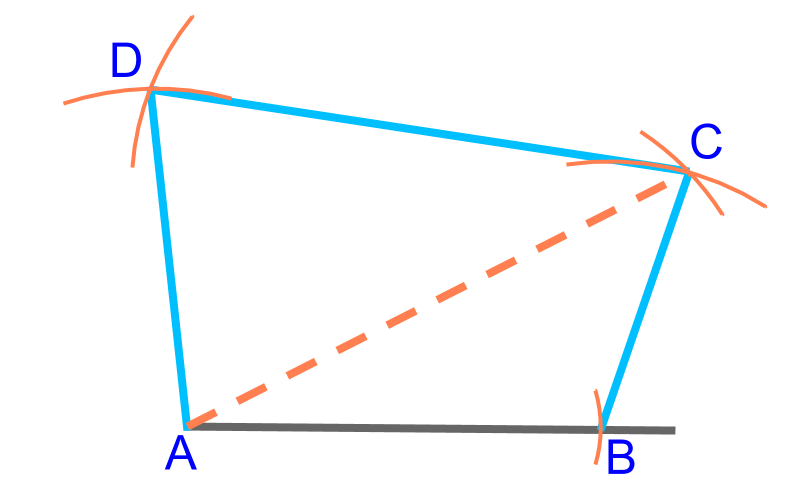
quadrilateral construction 4 sides and 1 diagonal

To construct a quadrilateral, 4 sides ( $\bar{A B}$ $bar(AB)$ , $\bar{B C}$ $bar(BC)$ , $\bar{C D}$ $bar(CD)$ , $\bar{A D}$ $bar(AD)$ ) and a diagonal ( $\bar{A C}$ $bar(AC)$ ) are given. This is illustrated in the figure. The quadrilateral can be constructed by considering this as two SSS triangles $A B C$ $ABC$ and $A C D$ $ACD$

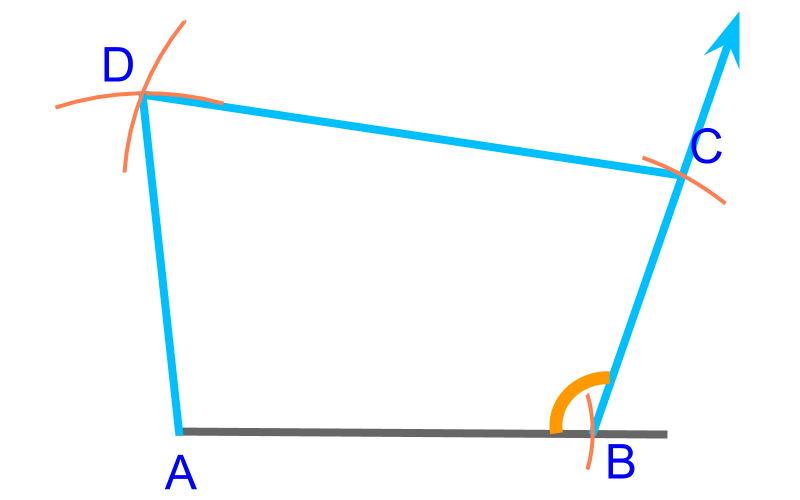
quadrilateral construction 4 sides and 1 angle

To construct a quadrilateral, 4 ( $\bar{A B}$ $bar(AB)$ , $\bar{B C}$ $bar(BC)$ , $\bar{C D}$ $bar(CD)$ , $\bar{A D}$ $bar(AD)$ ) sides and an angle ( $∠ B$ $/_B$ ) are given. This is illustrated in the figure. The quadrilateral can be constructed by considering this as an SAS triangle $A B C$ $ABC$ and another SSS triangle $A C D$ $ACD$

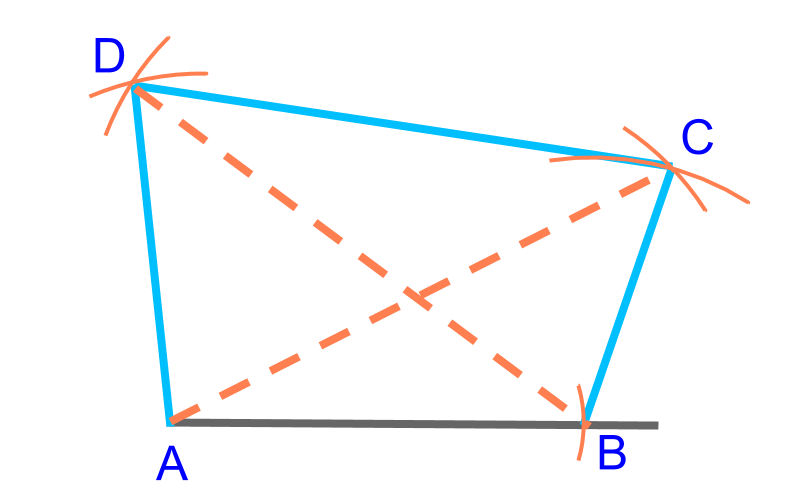
quadrilateral construction 3 sides and 2 diagonals

To construct a quadrilateral, $3$ $3$ ( $\bar{A B}$ $bar(AB)$ , $\bar{B C}$ $bar(BC)$ , $\bar{A D}$ $bar(AD)$ ) sides and two diagonals ( $\bar{A C}$ $bar(AC)$ , $\bar{B D}$ $bar(BD)$ ) are given. This is illustrated in the figure. The quadrilateral can be constructed by considering consider this as two SSS triangles $A B C$ $ABC$ and $A B D$ $ABD$

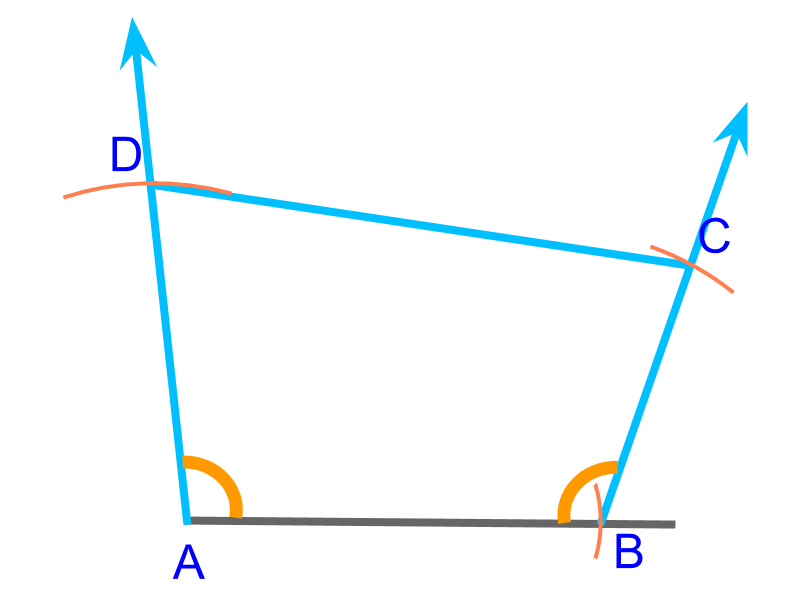
quadrilateral construction 3 sides and 2 angles

To construct a quadrilateral, $3$ $3$ sides ( $\bar{A B}$ $bar(AB)$ , $\bar{B C}$ $bar(BC)$ , $\bar{A D}$ $bar(AD)$ ) and $2$ $2$ angles ( $∠ A$ $/_A$ , $∠ B$ $/_B$ ) are given. This is illustrated in the figure. The quadrilateral can be constructed by considering this as two SAS triangles $A B C$ $ABC$ and $B A D$ $BAD$ .

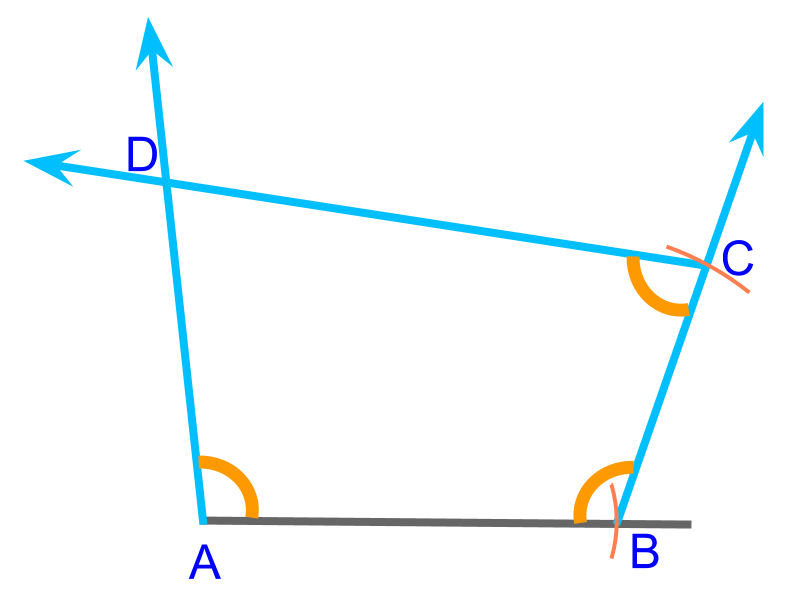
quadrilateral construction 2 sides and 3 angles

To construct a quadrilateral, $2$ $2$ sides ( $\bar{A B}$ $bar(AB)$ , $\bar{B C}$ $bar(BC)$ ) and $3$ $3$ angles ( $∠ A$ $/_A$ , $∠ B$ $/_B$ , $∠ C$ $/_C$ )are given. This is illustrated in the figure. To construct, "consider this as an SAS triangle $A B C$ $ABC$ and another ASA triangle with two angles $∠ C$ $/_C$ and $∠ A$ $/_A$ ". Note that $△ A C D$ $/_\ACD$ is formed by angles $∠ C$ $/_C$ and $∠ A$ $/_A$

summary

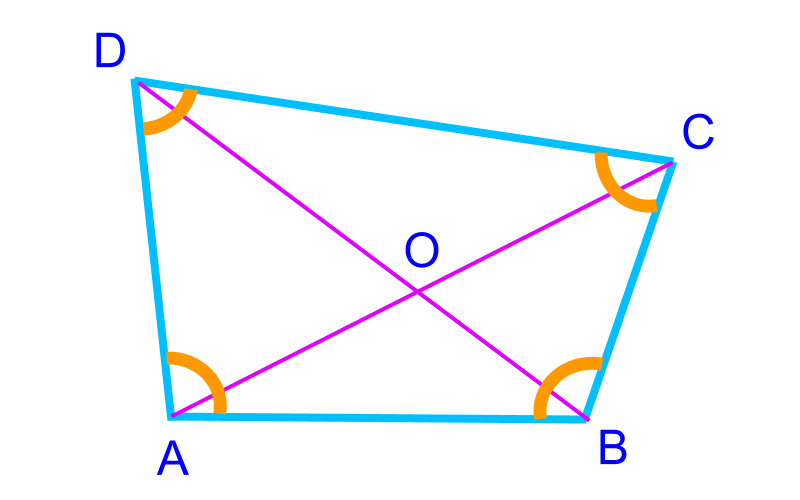
Construction of Quadrilateral : Properties of quadrilaterals

• sum of interior angles $360^{\circ}$ $360^@$

The formulations of questions

• 4 sides and a diagonal

• 3 sided and 2 diagonals

• 4 sides and an angle

• 3 sides and 2 angles

• 2 sides and 3 angles

Outline